
- •Часть 2
- •Методические указания
- •Часть 2
- •Введение
- •Занятие № 15
- •Интегрирование дифференциальных
- •Биномов. Подстановки чебышева.
- •Подстановки эйлера
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятия № 16 приложения определенного интеграла
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 17 условный экстремум. Метод множителей лагранжа. Наибольшее и наименьшее значения.Функции в замкнутой области
- •Контрольные вопросы и задания
- •Примеры решения задач
- •17.3. Задачи и упражнения для самостоятельного решения
- •Занятие № 18 дифференциальные уравнения, приводящиеся к однородным
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 19
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 20
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 21 дифференциальнЫе уравнения, допускающие понижение порядка.
- •Основные понятия
- •I. Уравнения вида
- •II. Уравнения вида , явно
- •III. Уравнения вида , явно
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 22 Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами со специальной правой частью
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 23
- •Решение Систем дифференциальных уравнений (метод исключения)
- •Литература: [1], с. 103-107.
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 24 Понятие о теории устойчивости ляпунова
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 25. Приближенное решение дифференциальных уравнений
- •Контрольные вопросы и задания
- •Заключение
- •Библиографический список
- •Часть 2
- •В авторской редакции
Примеры решения задач
Пример
1. Найти
интеграл
 .
.
Решение. Представим данный интеграл в следующем виде:
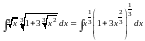 .
.
Отсюда
видно, что под знаком интеграла стоит
дифференциальный бином, при этом
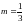 ,
,
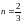 ,
,
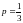 .
Так как
.
Так как
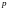 - не целое число, то данный интеграл не
относится к первому случаю.
- не целое число, то данный интеграл не
относится к первому случаю.
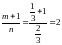 - целое число, поэтому данный интеграл
относится ко второму случаю и
соответствующая подстановка:
- целое число, поэтому данный интеграл
относится ко второму случаю и
соответствующая подстановка:
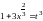 .
Выражаем отсюда
.
Выражаем отсюда
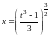 и находим
и находим
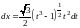 .
Таким образом,
.
Таким образом,
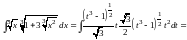

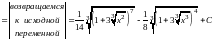 .
.
Пример
2. Найти
интеграл
 .
.
Решение. Представим данный интеграл в следующем виде:
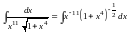 .
.
Отсюда
видно, что под знаком интеграла стоит
дифференциальный бином, при этом
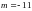 ,
,
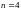 ,
,
 .
Так как
- не целое число, то данный интеграл не
относится к первому случаю.
.
Так как
- не целое число, то данный интеграл не
относится к первому случаю.
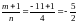 - не целое число, значит данный интеграл
не относится ко второму случаю.
- не целое число, значит данный интеграл
не относится ко второму случаю.
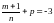 - целое число, поэтому данный интеграл
относится к третьему случаю и
соответствующая подстановка:
- целое число, поэтому данный интеграл
относится к третьему случаю и
соответствующая подстановка:
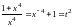 .
Выражаем отсюда
.
Выражаем отсюда
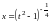 и находим
и находим
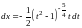 .
Таким образом,
.
Таким образом,
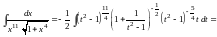

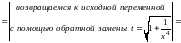
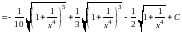 .
.
Пример
3. Найти
интеграл
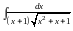 .
.
Решение.
Это интеграл вида
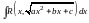 .
В нашем случае
.
В нашем случае
 ,
поэтому применим первую подстановку
Эйлера:
,
поэтому применим первую подстановку
Эйлера:
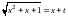 .
Возведя обе части равенства в квадрат,
получим
.
Возведя обе части равенства в квадрат,
получим
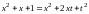 .
Выражаем отсюда
.
Выражаем отсюда
 и находим
и находим
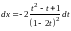 .
Таким образом,
.
Таким образом,
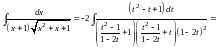


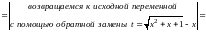
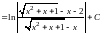 .
.
Пример
4. Найти
интеграл
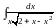 .
.
Решение.
Это интеграл вида
.
В нашем случае квадратный трехчлен
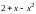 имеет действительные корни
имеет действительные корни
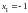 и
и
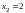 ,
поэтому применим третью подстановку
Эйлера:
,
поэтому применим третью подстановку
Эйлера:
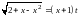 .
Возведя обе части равенства в квадрат,
получим
.
Возведя обе части равенства в квадрат,
получим
 .
Выражаем отсюда
.
Выражаем отсюда
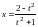 и находим
и находим
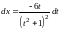 .
Таким образом,
.
Таким образом,


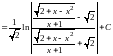 .
.
Задачи и упражнения для самостоятельного решения
Решить задачи: [3], 2076, 2078, 2080;
Форма отчетности: устный опрос, типовой расчет, контрольная работа.
Занятия № 16 приложения определенного интеграла
Литература: [1], c. 429-448;
Контрольные вопросы и задания
1. Как вычислить с помощью определенного интеграла площадь плоской фигуры в случае задания ее границы в явном виде, в полярных координатах, параметрическими уравнениями?
2. Вычислите с помощью определенного интеграла длину дуги кривой в случае задания ее уравнением в явном виде, параметрическом виде, в полярных координатах?
3.
Как вычислить объем тела по площадям
поперечных сечений; объем тела вращения
вокруг оси
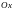 ,
оси
,
оси
 ?
?
5. Как вычислить поверхность тела вращения?
6. Как найти величину работы с помощью определенного интеграла?
7. Найдите координаты центра тяжести плоской линии, плоской фигуры?
Примеры решения задач
Пример 1. Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями
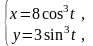
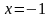
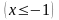 .
.
Решение.
Изобразим
данные линии и заштрихуем искомую
площадь (рис. 1). Найдем значения параметра
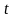 ,
соответствующие точкам пересечения
данных кривых. Для этого решаем уравнение
,
соответствующие точкам пересечения
данных кривых. Для этого решаем уравнение
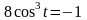 или
или
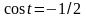 и получаем
и получаем
 (соответствует точке B)
и
(соответствует точке B)
и
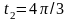 (соответствует точке C).
Точке A
соответствует
значение параметра
(соответствует точке C).
Точке A
соответствует
значение параметра
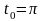 так как
так как
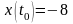 и
и
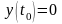 .
.
Р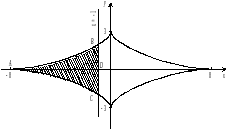 ис.
1
ис.
1
Площадь
фигуры
 находим как удвоенную площадь верхней
половины
находим как удвоенную площадь верхней
половины
 ,
интегрируя при этом в направлении
возрастания
,
интегрируя при этом в направлении
возрастания
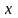 от точки
от точки
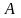 до точки
до точки
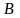 :
:
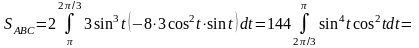
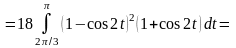


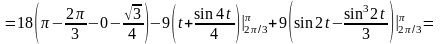
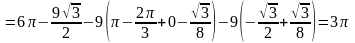 .
.
Пример
2. Найти
площадь фигуры, лежащей вне окружности
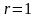 и ограниченной кривой
и ограниченной кривой
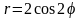 .
.
Решение.
Так как функция
имеет период
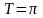 ,
то при изменении
,
то при изменении
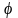 от
от
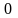 до
до
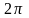 радиус-вектор описывает два равных
лепестка кривой. При этом допустимыми
для
являются те значения, при которых
радиус-вектор описывает два равных
лепестка кривой. При этом допустимыми
для
являются те значения, при которых
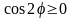 ,
откуда
,
откуда
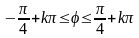
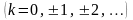 .
.
Следовательно,
один из лепестков описывается при
изменении
от
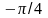 до
до
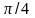 .
Второй лепесток получается при изменении
от
.
Второй лепесток получается при изменении
от
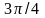 до
до
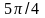 (рис. 10). Вырезая из лепестков части,
принадлежащие кругу
(рис. 10). Вырезая из лепестков части,
принадлежащие кругу
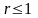 ,
мы получим фигуру, площадь которой нужно
определить. Ясно, что искомая площадь
,
мы получим фигуру, площадь которой нужно
определить. Ясно, что искомая площадь
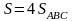 .
В свою очередь
.
В свою очередь
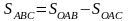 .
Точкам
и
.
Точкам
и
 соответствует значение полярного угла
соответствует значение полярного угла
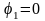 .
Найдем полярные координаты точки
пересечения данных кривых. Для этого
решим уравнение
.
Найдем полярные координаты точки
пересечения данных кривых. Для этого
решим уравнение
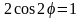 т.е.
т.е.
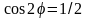 .
Между
и
находится только корень
.
Между
и
находится только корень
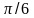 .
Таким образом, точке
соответствует полярный угол
.
Таким образом, точке
соответствует полярный угол
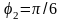 .
.

Рис. 2
Далее определяем искомую площадь:
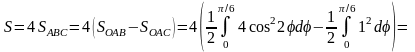
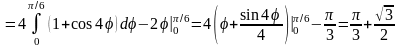 .
.
Пример
3. Вычислить
площадь фигуры, ограниченной кривыми
 и
и
 .
.
Решение.
Так как
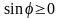 при
при
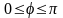 ,
то первая кривая лежит в верхней
полуплоскости и проходит через полюс
,
то первая кривая лежит в верхней
полуплоскости и проходит через полюс
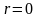 .
Чтобы построить ее перейдем в декартовые
координаты, пользуясь соотношениями
.
Чтобы построить ее перейдем в декартовые
координаты, пользуясь соотношениями
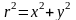 и
и
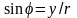 .
Получаем
.
Получаем
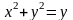 .
Приведя это уравнение к каноническому
виду, будем иметь
.
Приведя это уравнение к каноническому
виду, будем иметь
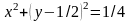 .
Это уравнение окружности с центром
.
Это уравнение окружности с центром
 и радиусом равным
и радиусом равным
 (рис. 11). Вторая кривая определена при
(рис. 11). Вторая кривая определена при
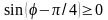 т.е. при
т.е. при
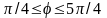 и также проходит через полюс
.
Преобразуем уравнение второй кривой
и также проходит через полюс
.
Преобразуем уравнение второй кривой

и перейдем в декартовые координаты
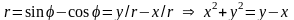 .
.
Приведем
полученное уравнение к каноническому
виду:
 .
Видно, что это уравнение окружности с
центром
.
Видно, что это уравнение окружности с
центром
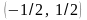 и радиусом равным
и радиусом равным
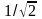 (рис. 2).
(рис. 2).
Из
вышесказанного следует, что полюс есть
точка пересечения окружностей. Другая
точка пересечения окружностей находится
из решения уравнения
 или
или
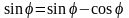 ,
откуда
,
откуда
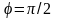 .
Из рис. 3 видно, что искомая площадь S
равна сумме площадей сегментов
.
Из рис. 3 видно, что искомая площадь S
равна сумме площадей сегментов
 и
и
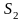 ,
причем сегменты примыкают друг к другу
по лучу
.
Дуга первого сегмента описывается
концом полярного радиуса второй
окружности при
,
причем сегменты примыкают друг к другу
по лучу
.
Дуга первого сегмента описывается
концом полярного радиуса второй
окружности при
 ,
поэтому его площадь
,
поэтому его площадь

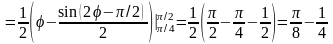 .
.
Р ис.
3
ис.
3
Дуга
второго сегмента описывается концом
полярного радиуса первой окружности
при
 ,
поэтому его площадь
,
поэтому его площадь
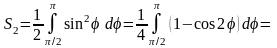
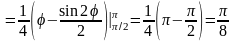 .
.
Таким
образом, искомая площадь
 .
.
Пример
4. Найти
площадь фигуры, ограниченной кривыми
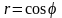 и
и
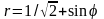 .
.
Решение.
Определим область, в которой расположена
первая кривая. Для этого решим неравенство
 .
Получаем
.
Получаем
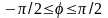 .
Так как
.
Так как
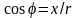 ,
то в декартовых координатах уравнение
первой кривой запишется следующим
образом
,
то в декартовых координатах уравнение
первой кривой запишется следующим
образом
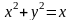 или в каноническом виде
или в каноническом виде
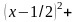
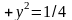 – это уравнение окружности с центром
– это уравнение окружности с центром
 и радиусом равным
.
Окружность расположена в правой
полуплоскости и проходит через полюс
(рис. 4).
и радиусом равным
.
Окружность расположена в правой
полуплоскости и проходит через полюс
(рис. 4).
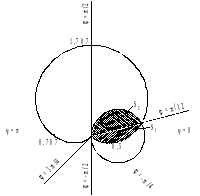
Рис. 4
Для
построения второй кривой решаем
неравенство
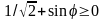 .
Получаем
.
Получаем
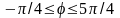 .
Видно, что при граничных значениях
полярного угла
,
а при
достигает максимального значения
.
Видно, что при граничных значениях
полярного угла
,
а при
достигает максимального значения
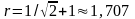 (рис. 4).
(рис. 4).
Из вышеизложенного следует, что одной точкой пересечения данных кривых является полюс. Найдем остальные точки пересечения кривых. Для этого решим систему
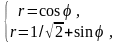
 .
.
Здесь указан диапазон углов, общих для обеих кривых. Приравнивая правые части уравнений, получаем
 ,
,
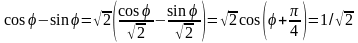 ,
,
 ,
,
 ,
,
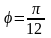 .
.
Из
рис. 12 видно, что искомая площадь равна
сумме площадей
и
двух сегментов, причем сегменты примыкают
друг к другу по лучу
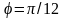 .
Дуга первого сегмента описывается
концом полярного радиуса
при изменении полярного угла
от
до
.
Дуга первого сегмента описывается
концом полярного радиуса
при изменении полярного угла
от
до
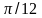 ,
поэтому
,
поэтому
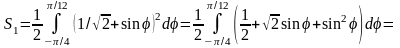

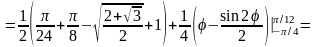
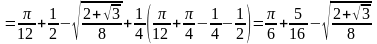 .
.
Дуга
второго сегмента описывается концом
полярного радиуса
при изменении полярного угла
от
до
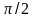 ,
поэтому
,
поэтому
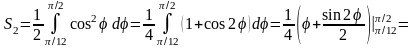
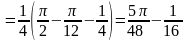 .
.
Таким образом, искомая площадь равна
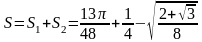 .
.
Задачи и упражнения для самостоятельного решения
Решить задачи: [6], 6.456, 6.470, 6.478, 6.480, 6.485, 6.494, 6.502, 6.509, 6.512, 6.521, 6.534, 6.535, 6.537, 6.562, 6.575.
Форма отчетности: устный опрос, контрольная работа, коллоквиум.
