Занятие № 17 условный экстремум. Метод множителей лагранжа. Наибольшее и наименьшее значения.Функции в замкнутой области
Литература: [1], с. 272-276; [3], с. 434-437.
Контрольные вопросы и задания
1. Какова постановка задачи на нахождение условного экстремума функции нескольких переменных?
2. Каковы необходимые условия условного экстремума? Докажите их.
3. В чем состоит метод множителей Лагранжа? Что такое функция Лагранжа?
4. Каковы достаточные условия условного экстремума?
5. Как по знаку второго дифференциала вспомогательной функции определить характер условного экстремума?
6. Как найти наибольшее или наименьшее значение функции нескольких переменных в замкнутой области?
7. Какие точки функции называются стационарными?
8. Как исследуются функции на границе области?
9. Как задача на нахождение наибольшего, наименьшего значения в замкнутой области связана с задачей на условный экстремум?
Примеры решения задач
Пример
1. Найти
наибольшее и наименьшее значения функции
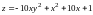на отрезке
,
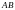если координаты точек
,
.
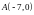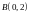Решение.
Уравнение прямой
в отрезках
.
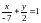Таким образом, получаем задачу на
условный экстремум: найти экстремум
функции
при условии
.
Составляем функцию Лагранжа:
.
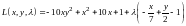Ищем стационарные точки этой функции:
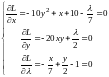
Первое
уравнение умножим на 7, второе на 2 и
сложим их. Этим исключим параметр
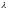из системы:
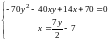
Непосредственной
подстановкой приходим к уравнению,
которое после сокращений имеет вид
.
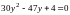Отсюда находим
,
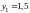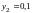и из системы получаем точки
,
,
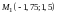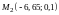принадлежащие отрезку
.
Вычисляем значения функции в стационарных точках
,
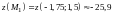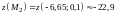
и на концах отрезка
,
.
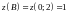Сравнивая
все полученные величины, приходим к
выводу: наибольшее значение функции на
отрезке достигается в точке
,
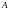а наименьшее в точке
.
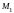Пример
2. Найти
наибольшее и наименьшее значения функции
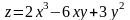в замкнутой области, ограниченной осью
,
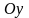прямой
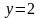и параболой
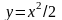при
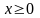(рис. 5).
Решение.
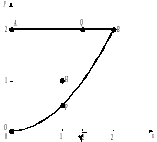
Рис. 5
1) Находим стационарные точки функции.
;
.
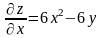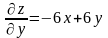Решив систему уравнений
,
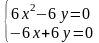получим
две стационарные точк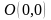и
и
.
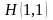Первая из них принадлежит границе
области. Следовательно, если функция
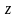принимает наибольшее (наименьшее)
значение во внутренней точке области,
то это может быть только в точке
.
Найдем
.
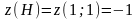2) Исследуем функцию на границе области
а)
на отрезке
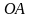имеем
,
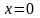поэтому
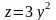
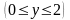- возрастающая функция одной переменой
;
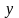наибольшее и наименьшее значения она
принимает на концах отрезка
.
Найдем
б)
на отрезке
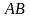имеем
,
следовательно,
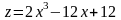
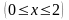представляет функцию одной переменной
;
ее наибольшее и наименьшее значения
находятся среди ее значений в критических
точках и на концах отрезка. Решая
уравнение
,
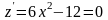находим
.
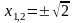Внутри отрезка
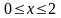имеется лишь одна критическая точка
;
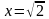соответствующей точкой отрезка
является точка
.
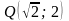Итак, наибольшее и наименьшее значения
функции
на отрезке
находятся среди ее значений в точках
,
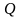и
.
Найдем
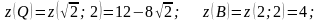
в)
на дуге
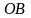параболы
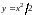имеем
.
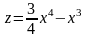Решая уравнение
,
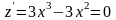получим
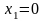и
;
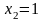соответствующими точками параболы
являются точки
и
.
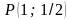Таким образом, наибольшее и наименьшее
значения функции
на дуге
находятся среди ее значений в точках
,
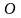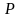и
.
Найдем
.
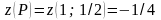3)
Сравнивая значения функции
в точках
,
,
,
,
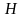и
,
получим решение задачи
.