
- •Часть 2
- •Методические указания
- •Часть 2
- •Введение
- •Занятие № 15
- •Интегрирование дифференциальных
- •Биномов. Подстановки чебышева.
- •Подстановки эйлера
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятия № 16 приложения определенного интеграла
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 17 условный экстремум. Метод множителей лагранжа. Наибольшее и наименьшее значения.Функции в замкнутой области
- •Контрольные вопросы и задания
- •Примеры решения задач
- •17.3. Задачи и упражнения для самостоятельного решения
- •Занятие № 18 дифференциальные уравнения, приводящиеся к однородным
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 19
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 20
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 21 дифференциальнЫе уравнения, допускающие понижение порядка.
- •Основные понятия
- •I. Уравнения вида
- •II. Уравнения вида , явно
- •III. Уравнения вида , явно
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 22 Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами со специальной правой частью
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 23
- •Решение Систем дифференциальных уравнений (метод исключения)
- •Литература: [1], с. 103-107.
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 24 Понятие о теории устойчивости ляпунова
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 25. Приближенное решение дифференциальных уравнений
- •Контрольные вопросы и задания
- •Заключение
- •Библиографический список
- •Часть 2
- •В авторской редакции
Примеры решения задач
Пример.
Найти общее решение дифференциального
уравнения
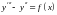 ,
где а)
,
где а) 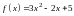 ,
б)
,
б) 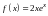 ,
в)
,
в)
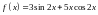 .
.
Решение.
Характеристическое уравнение
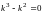 имеет корни
имеет корни
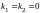 и
и
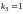 .
Поэтому общее решение однородного
уравнения
.
Поэтому общее решение однородного
уравнения
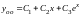 .
Найдем частные решения неоднородного
уравнения для случаев а) – в).
.
Найдем частные решения неоднородного
уравнения для случаев а) – в).
а)
Контрольное число
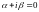 – корень характеристического уравнения
кратности 2 и в правой части стоит
многочлен второй степени. Поэтому
частное решение неоднородного уравнения
будем искать в виде
– корень характеристического уравнения
кратности 2 и в правой части стоит
многочлен второй степени. Поэтому
частное решение неоднородного уравнения
будем искать в виде
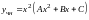 .
Для определения неизвестных коэффициентов
,
.
Для определения неизвестных коэффициентов
,
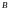 ,
,
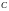 вычисляем
вычисляем
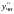 ,
,
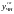 и подставляем их в исходное уравнение.
Получаем
и подставляем их в исходное уравнение.
Получаем
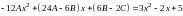 ,
откуда имеем систему уравнений
,
откуда имеем систему уравнений
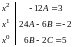
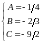 .
.
Следовательно
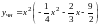 .
.
б)
Контрольное число
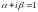 – корень характеристического уравнения
кратности 1 и в правой части стоит
произведение экспоненты на многочлен
первой степени. Поэтому частное решение
неоднородного уравнения будем искать
в виде
– корень характеристического уравнения
кратности 1 и в правой части стоит
произведение экспоненты на многочлен
первой степени. Поэтому частное решение
неоднородного уравнения будем искать
в виде
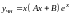 .
Для определения неизвестных коэффициентов
,
вычисляем
,
и подставляем их в исходное уравнение.
Получаем
.
Для определения неизвестных коэффициентов
,
вычисляем
,
и подставляем их в исходное уравнение.
Получаем

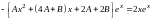 или
или
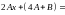
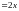 ,
откуда имеем систему уравнений
,
откуда имеем систему уравнений
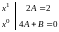
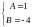 .
.
Следовательно
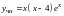 .
.
в)
Контрольное число
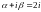 не является корнем характеристического
уравнения и в правой части стоят
произведения синуса и косинуса на
многочлены, старшая степень которых
равна 1. Поэтому частное решение
неоднородного уравнения будем искать
в виде
не является корнем характеристического
уравнения и в правой части стоят
произведения синуса и косинуса на
многочлены, старшая степень которых
равна 1. Поэтому частное решение
неоднородного уравнения будем искать
в виде
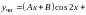
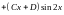 .
Для определения неизвестных коэффициентов
,
,
,
.
Для определения неизвестных коэффициентов
,
,
,
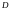 вычисляем
,
и подставляем их в исходное уравнение.
Получаем
вычисляем
,
и подставляем их в исходное уравнение.
Получаем
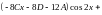

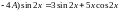 или
или

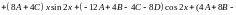
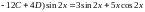 ,
откуда имеем систему уравнений
,
откуда имеем систему уравнений
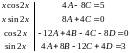
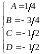 .
.
Следовательно
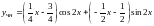 .
.
Таким образом, общие решения неоднородного уравнения для случаев а) – в) имеют вид:
а)
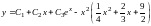 ;
;
б)
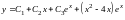 ;
;
в)
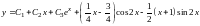 .
.
Задачи и упражнения для самостоятельного решения
Решить задачи: №№ 4314–4321 [2].
Форма отчетности: устный опрос, контрольная работа, типовой расчет.
Занятие № 23
Решение Систем дифференциальных уравнений (метод исключения)
Литература: [1], с. 103-107.
Основные понятия
Система дифференциальных уравнений первого порядка, разрешенных относительно производной, т.е. система вида
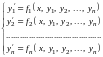 ,
(6.1)
,
(6.1)
где
– независимая переменная, а
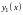 ,
,
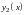 ,
,
,
,
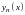 – неизвестные функции от
,
называется нормальной
системой.
Нормальную систему можно привести к
одному уравнению порядка
(или меньше) относительно одной неизвестной
функции, например
,
при помощи следующего алгоритма,
называемого метод
исключения.
– неизвестные функции от
,
называется нормальной
системой.
Нормальную систему можно привести к
одному уравнению порядка
(или меньше) относительно одной неизвестной
функции, например
,
при помощи следующего алгоритма,
называемого метод
исключения.
Дифференцируем
первое уравнение системы (6.1) по переменной
:
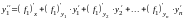 .
Производные
.
Производные
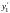 ,
,
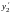 ,
,
,
,
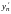 в правой части этого равенства заменим
их выражениями из системы (6.1). Получим
уравнение
в правой части этого равенства заменим
их выражениями из системы (6.1). Получим
уравнение
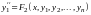 .
Это равенство дифференцируем по
:
.
Это равенство дифференцируем по
:
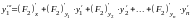 .
Производные
,
,
,
в правой части этого равенства заменим
их выражениями из системы (6.1). Получим
еще одно уравнение
.
Производные
,
,
,
в правой части этого равенства заменим
их выражениями из системы (6.1). Получим
еще одно уравнение
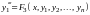 .
Это уравнение также дифференцируем по
и так далее до тех пор, пока не придем к
уравнению
.
Это уравнение также дифференцируем по
и так далее до тех пор, пока не придем к
уравнению
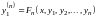 .
Полученные таким образом дифференциальные
уравнения объединим в одну систему, к
которой присоединим первое уравнение
системы (6.1):
.
Полученные таким образом дифференциальные
уравнения объединим в одну систему, к
которой присоединим первое уравнение
системы (6.1):
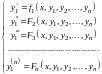 .
(6.2)
.
(6.2)
Первые
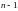 уравнений системы (6.2) разрешим относительно
переменных
,
уравнений системы (6.2) разрешим относительно
переменных
,
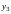 ,
,
,
выражая их через переменные
и
,
а также производные
,
,
,
,
выражая их через переменные
и
,
а также производные
,
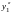 ,
,
,
,
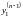 .
Полученные выражения подставим в
последнее уравнение системы (6.2). В итоге
придем к дифференциальному уравнению
порядка
относительно одной неизвестной функции
.
Из общего решения этого уравнения можно
получить общее решение системы (6.1).
Заметим, что порядок последнего уравнения
может быть меньше, чем
,
если при его получении были использованы
не все уравнения системы (6.1).
.
Полученные выражения подставим в
последнее уравнение системы (6.2). В итоге
придем к дифференциальному уравнению
порядка
относительно одной неизвестной функции
.
Из общего решения этого уравнения можно
получить общее решение системы (6.1).
Заметим, что порядок последнего уравнения
может быть меньше, чем
,
если при его получении были использованы
не все уравнения системы (6.1).
