
- •Часть 2
- •Методические указания
- •Часть 2
- •Введение
- •Занятие № 15
- •Интегрирование дифференциальных
- •Биномов. Подстановки чебышева.
- •Подстановки эйлера
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятия № 16 приложения определенного интеграла
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 17 условный экстремум. Метод множителей лагранжа. Наибольшее и наименьшее значения.Функции в замкнутой области
- •Контрольные вопросы и задания
- •Примеры решения задач
- •17.3. Задачи и упражнения для самостоятельного решения
- •Занятие № 18 дифференциальные уравнения, приводящиеся к однородным
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 19
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 20
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 21 дифференциальнЫе уравнения, допускающие понижение порядка.
- •Основные понятия
- •I. Уравнения вида
- •II. Уравнения вида , явно
- •III. Уравнения вида , явно
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 22 Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами со специальной правой частью
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 23
- •Решение Систем дифференциальных уравнений (метод исключения)
- •Литература: [1], с. 103-107.
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 24 Понятие о теории устойчивости ляпунова
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 25. Приближенное решение дифференциальных уравнений
- •Контрольные вопросы и задания
- •Заключение
- •Библиографический список
- •Часть 2
- •В авторской редакции
Занятие № 22 Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами со специальной правой частью
Литература: [1], c.79-80, 92-94; [3], c.135.
Указание. Перед изучением этой темы повторить тему "Решение линейных неоднородных дифференциальных уравнений с постоянными коэффициентами второго порядка".
Основные понятия
Линейные дифференциальные уравнения с постоянными коэффициентами имеют вид
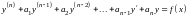 .
.
Общее
решение таких уравнений представляется
в виде суммы
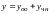 ,
где
,
где
 – общее
решение соответствующего
однородного
уравнения,
– общее
решение соответствующего
однородного
уравнения,
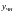 – частное
решение неоднородного уравнения.
– частное
решение неоднородного уравнения.
Для решения однородного уравнения составляется характеристическое уравнение
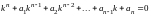
и
находятся его корни
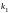 ,
,
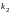 ,
,
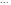 ,
,
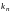 .
По характеру корней записываются частные
линейно независимые решения, руководствуясь
тем, что
.
По характеру корней записываются частные
линейно независимые решения, руководствуясь
тем, что
а)
каждому действительному однократному
корню
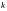 соответствует частное решение
соответствует частное решение
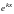 ;
;
б)
каждой паре комплексных сопряженных
однократных корней
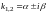 соответствуют два частных решения
соответствуют два частных решения
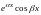 и
и
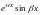 ;
;
в)
каждому действительному корню
кратности
 соответствует
линейно независимых частных решений
,
соответствует
линейно независимых частных решений
,
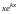 ,
,
,
,
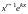 ;
;
г)
каждой паре комплексно сопряженных
корней кратности
соответствует
 частных решений
частных решений
,
 ,
,
,
,
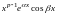 ,
,
,
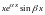 ,
,
,
,
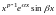 .
.
Найдя
все
 линейно независимых частных решений
линейно независимых частных решений
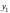 ,
,
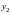 ,
,
,
,
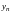 ,
строим общее решение однородного
уравнения
,
строим общее решение однородного
уравнения
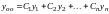 ,
,
где
,
,
,
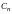 – произвольные постоянные.
– произвольные постоянные.
В
тех случаях, когда правая часть
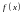 имеет специальный вид, частное решение
неоднородного уравнения находится
методом
неопределенных коэффициентов.
Этот метод сводится к следующим двум
случаям.
имеет специальный вид, частное решение
неоднородного уравнения находится
методом
неопределенных коэффициентов.
Этот метод сводится к следующим двум
случаям.
Случай
1. Правая
часть
 ,
где
,
где
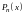 – многочлен степени
.
– многочлен степени
.
а)
Если
 не является корнем характеристического
уравнения, то частное решение ищется в
виде
не является корнем характеристического
уравнения, то частное решение ищется в
виде
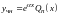 ,
где
,
где
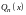 – многочлен степени
с неизвестными коэффициентами.
– многочлен степени
с неизвестными коэффициентами.
б)
Если
является корнем характеристического
уравнения кратности
,
то частное решение ищется в виде
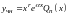 ,
где
– многочлен степени
с неизвестными коэффициентами.
,
где
– многочлен степени
с неизвестными коэффициентами.
В
частности, если
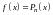 ,
т.е.
,
т.е.
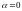 ,
то
ищется в виде
,
то
ищется в виде
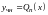 (если
не является корнем характеристического
уравнения) или в виде
(если
не является корнем характеристического
уравнения) или в виде
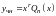 (если
является корнем характеристического
уравнения кратности
).
(если
является корнем характеристического
уравнения кратности
).
Случай
2.
 .
.
а)
Если
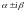 не являются корнями характеристического
уравнения, то
не являются корнями характеристического
уравнения, то
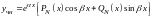 ,
где
,
где
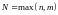 .
.
б)
Если
– корни характеристического уравнения
кратности
,
то
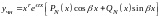 .
.
В
частности, если
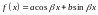 ,
т.е.
,
т.е.
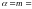
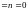 ,
то частное решение ищется в виде
,
то частное решение ищется в виде
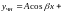
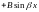 (если
не являются корнями характеристического
уравнения) или в виде
(если
не являются корнями характеристического
уравнения) или в виде
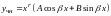 (если числа
– корни характеристического уравнения
кратности
).
(если числа
– корни характеристического уравнения
кратности
).
Контрольные вопросы и задания
1. Какова структура общего решения неоднородного уравнения?
2. Что такое характеристическое уравнение и как оно составляется для линейного однородного дифференциального уравнения с постоянными коэффициентами?
3. Как строится общее решение однородного уравнения в зависимости от характера корней характеристического уравнения?
4. Какой вид правой части неоднородного уравнения называют специальным?
5. Как по виду правой части записывается частное решение неоднородного уравнения с неопределенными коэффициентами?
6. В чем состоит метод неопределенных коэффициентов нахождения частного решения неоднородного уравнения?
