
- •Часть 2
- •Методические указания
- •Часть 2
- •Введение
- •Занятие № 15
- •Интегрирование дифференциальных
- •Биномов. Подстановки чебышева.
- •Подстановки эйлера
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятия № 16 приложения определенного интеграла
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 17 условный экстремум. Метод множителей лагранжа. Наибольшее и наименьшее значения.Функции в замкнутой области
- •Контрольные вопросы и задания
- •Примеры решения задач
- •17.3. Задачи и упражнения для самостоятельного решения
- •Занятие № 18 дифференциальные уравнения, приводящиеся к однородным
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 19
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 20
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 21 дифференциальнЫе уравнения, допускающие понижение порядка.
- •Основные понятия
- •I. Уравнения вида
- •II. Уравнения вида , явно
- •III. Уравнения вида , явно
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 22 Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами со специальной правой частью
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 23
- •Решение Систем дифференциальных уравнений (метод исключения)
- •Литература: [1], с. 103-107.
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 24 Понятие о теории устойчивости ляпунова
- •Основные понятия
- •Контрольные вопросы и задания
- •Примеры решения задач
- •Занятие № 25. Приближенное решение дифференциальных уравнений
- •Контрольные вопросы и задания
- •Заключение
- •Библиографический список
- •Часть 2
- •В авторской редакции
17.3. Задачи и упражнения для самостоятельного решения
Решить задачи: [6], 3.25, 3.26, 3.27, 3.28, 3.35, 3.36, 3.37, 3.38.
Форма отчетности: устный опрос, контрольная работа.
Занятие № 18 дифференциальные уравнения, приводящиеся к однородным
Литература: [1], c. 25-30; [3], c. 113-114.
Основные понятия
Дифференциальные уравнения вида
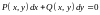 (1.1)
(1.1)
называются
однородными,
если
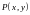 и
и
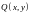 являются однородными
функциями одного и того же измерения
являются однородными
функциями одного и того же измерения
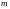 ,
т.е. при любом
выполняются тождества
,
т.е. при любом
выполняются тождества
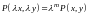 и
и
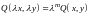 .
.
В
этом случае уравнение (1.1) можно привести
к виду
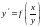 и с помощью подстановки
и с помощью подстановки
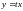 однородное уравнение приводится к
уравнению с разделяющимися переменными
относительно новой переменной
однородное уравнение приводится к
уравнению с разделяющимися переменными
относительно новой переменной
 .
.
Уравнение
вида
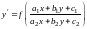 ,
для которого
,
для которого
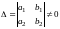 ,
приводится к однородному подстановкой
,
приводится к однородному подстановкой
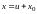 ,
,
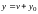 ,
где
,
где
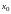 и
и
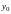 находятся из решения системы
находятся из решения системы
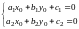 .
При
.
При
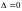 делается подстановка
делается подстановка
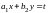 ,
которая позволяет разделить переменные.
,
которая позволяет разделить переменные.
Контрольные вопросы и задания
1. Какие уравнения первого порядка называются однородными?
2. Как решаются такие уравнения?
3. Укажите вид уравнений, приводящихся к однородным.
4. Какие два случая различают при решении таких уравнений? Каков алгоритм решения в каждом из этих случаев?
Примеры решения задач
Пример. Решить дифференциальное уравнение
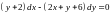 .
.
Решение.
Приведем уравнение к виду
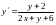 .
Это уравнение можно привести к однородному.
Сделаем подстановку
,
.
Подберем
и
так, чтобы
.
Это уравнение можно привести к однородному.
Сделаем подстановку
,
.
Подберем
и
так, чтобы
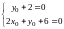 .
Решая систему, находим
.
Решая систему, находим
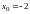 ,
,
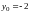 .
Тогда исходное уравнение принимает вид
.
Тогда исходное уравнение принимает вид
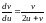 ,
т.е. является однородным. Совершая
подстановку
,
т.е. является однородным. Совершая
подстановку
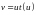 ,
получим
,
получим
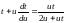 .
Далее, разделив переменные, получим
уравнение
.
Далее, разделив переменные, получим
уравнение
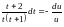 ,
проинтегрировав которое будем иметь
,
проинтегрировав которое будем иметь
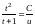 .
Учитывая, что
.
Учитывая, что
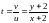 записываем общий интеграл исходного
дифференциального уравнения
записываем общий интеграл исходного
дифференциального уравнения
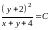 .
.
Разберите также решения примеров № 552, 553 [3].
Задачи и упражнения для самостоятельного решения
1)
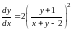 ;
2)
;
2)
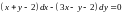 ;
;
3)
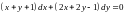 ;
4)
;
4)
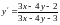 .
.
5)
Определить кривые, у которых отрезок
касательной от точки касания
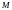 до пересечения с осью
равен отрезку, отсекаемому касательной
от оси
.
до пересечения с осью
равен отрезку, отсекаемому касательной
от оси
.
Форма отчетности: устный опрос, типовой расчет.
Занятие № 19
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ БЕРНУЛЛИ
Литература: [1], c. 30-35.
Основные понятия
Уравнением Бернулли называется уравнение вида
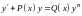 ,
(2.1)
,
(2.1)
где
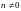 и
и
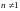 .
Это уравнение с помощью замены
.
Это уравнение с помощью замены
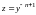 приводится к линейному
относительно функции
приводится к линейному
относительно функции
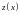
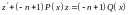 .
.
Получившееся
линейное уравнение можно решить методом
Бернулли,
полагая
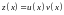 ,
или методом
Лагранжа,
решая сначала соответствующее однородное
уравнение, а затем производя вариацию
произвольной постоянной.
,
или методом
Лагранжа,
решая сначала соответствующее однородное
уравнение, а затем производя вариацию
произвольной постоянной.
Уравнение
Бернулли можно, не сводя к линейному,
проинтегрировать с помощью подстановки
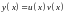 (т.е. методом Бернулли) или применив
метод вариации произвольной постоянной
(метод Лагранжа).
(т.е. методом Бернулли) или применив
метод вариации произвольной постоянной
(метод Лагранжа).
Контрольные вопросы и задания
1. Какие уравнения первого порядка называются линейными?
2. Какими методами решаются линейные дифференциальные уравнения?
3. В чем состоит метод Бернулли?
4. В чем состоит метод Лагранжа?
3. Какой вид имеет уравнение Бернулли?
4. Как уравнения Бернулли приводятся к линейным уравнениям?
5. Можно ли решать уравнение Бернулли, не приводя его к линейному виду?
