3.3. Другие связки (операции)
Новые
высказывания могут быть образованы при
помощи нескольких логических операций
и составлять формулы. В качестве
часто употребляемых, например, в теории
автоматов (цифровой радиоэлектронике),
можно указать Штрих Шеффера (│), Стрелку
Пирса (↓) и сумму по модулю два (
).
Штрих
Шеффера, или антиконъюнкция
обозначается
│
и соответствует связке
.
Таблица истинности штриха Шеффера имеет
вид:
Таблица 7.
-
│
0
0
1
0
1
1
1
0
1
1
1
0
Стрелка
Пирса, или антидизъюнкция обозначается
,
по определению соответствует связке
.
Таблица истинности стрелки Пирса.
Таблица 8.
-
0
0
1
0
1
0
1
0
0
1
1
0
Сумма по
модулю два, или антиэквивалентность,
по определению
.
Таблица истинности суммы по модулю два
имеет вид:
Таблица 9.
-
X
Y
X Y
0
0
0
0
1
1
1
0
1
1
1
0
Пример 3.3. Представить логической формулой высказывание «Сегодня четверг или пятница». Высказывание - «сегодня четверг», высказывание - «сегодня пятница». Высказыванию «Сегодня четверг или пятница» соответствует формула .
3.4. Основные законы, определяющие свойства введенных логических операций.
Формула высказываний называется тавтологией, тождественно истинной, общезначимой формулой, если при подстановке вместо переменных высказываний любых конкретных высказываний она превращается всегда в истинное высказывание.
Формула высказываний называется противоречием, неразрешимой или тождественно ложной, если при подстановке вместо переменных высказываний любых конкретных высказываний она превращается всегда в ложное высказывание.
Формула высказываний называется разрешимой (выполнимой), если может превращаться как в истинное, так и ложное высказывание.
Перечислим основные законы (тавтологии), определяющие свойства введенных логических операций:
1) Идемпотентность дизъюнкции и конъюнкции:
,
.
2) Коммутативность дизъюнкции и конъюнкции:
,
.
3) Ассоциативность дизъюнкции и конъюнкции:
,
.
4) Дистрибутивность операций дизъюнкции и конъюнкции относительно друг друга:
,
.
5) Двойное отрицание:
.
6) Закон Моргана:
,
.
7) Склеивание:
,
.
8) Поглощение:
,
.
9) Действие с логическими константами 0 и 1:
,
,
,
,
.
10) Закон исключения третьего:
.
11) Тождество:
X↔X.
12) Отрицание противоречия:
.
13) Контрапозиция:
.
14) Цепное заключение:
.
15) Противоположность:
.
16) Модус поненс (ponens):
.
Сформулированные законы легко проверить с помощью таблицы истинности.
Докажем, что
формула
,
соответствующая контрапозиции, является
тавтологией. Составим соответствующую
таблицу истинности.
Таблица 10.
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
Так как в последнем столбце стоят только единицы, то формула является тавтологией.
Если известно, что высказывания имеют одинаковые таблицы истинности, то такие высказывания являются равносильными (эквивалентными).
На практике для доказательства равносильности пользуются признаками равносильности:
1. Две формулы и равносильны тогда и только тогда, если каждая из них является логическим следствием другой.
2. Две формулы
и
равносильны тогда и только тогда, когда
формула
- тавтология.
Заметим, что при исследовании различных высказываний на эквивалентность ( равносильность) логическую связку ↔ можно заменить обычным знаком равенства =.
Полезным
оказывается правило исключения
логических символов
и
:
для каждой формулы можно указать
равносильную ей формулу, не содержащую
логических символов
и
.
Из следующей таблицы истинности видно,
что X→Y
эквивалентно
.
Таблица 11.
-
X
Y
X→Y
0
0
1
1
0
1
1
1
1
0
0
0
1
1
1
1
Задачи по теме “Логические операции»
Задача 1.
Докажите тождественную истинность
формулы.
.
Решение. Составим таблицу истинности:
Таблица 12.
-
X
Y
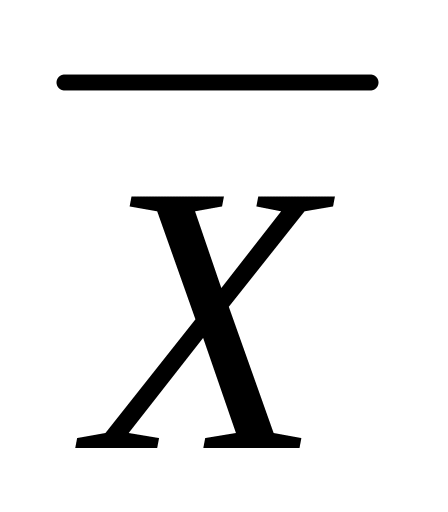
0
0
1
1
1
0
1
1
1
1
1
0
0
0
1
1
1
0
1
1
Последний столбец состоит из 1, ч.т.д.
Задача 2.
Докажите эквивалентность
.
Решение. Пусть
.
Составим таблицу истинности:
Таблица 13.
X |
Y |
Z |
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Пусть
.
Таблица 14.
X |
Y |
Z |
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Поскольку
таблицы истинности для
и
совпадают, то эквивалентность
доказана.
Задача 3.
Для высказывания «Если Иван умен, а
Василий глуп, то Иван будет победителем»
найдите логическую формулу и постройте
таблицу истинности. Воспользуйтесь
буквенными обозначениями:
для «Иван умен»,
для «Василий глуп»,
для
«Иван будет победителем».
Решение.
Логическая формула имеет вид:
.
Таблица истинности имеет вид:
Таблица 15.
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
Задача 4. Для высказывания «Если Василий глуп, а Иван не будет победителем, то Иван не умен» найдите логическую формулу и постройте таблицу истинности. Воспользуйтесь буквенными обозначениями: для «Иван умен», для «Василий глуп», для «Иван будет победителем».
Решение.
Логическая формула имеет вид:
.
Таблица истинности имеет вид:
Таблица 16.
-
X
Y
Z
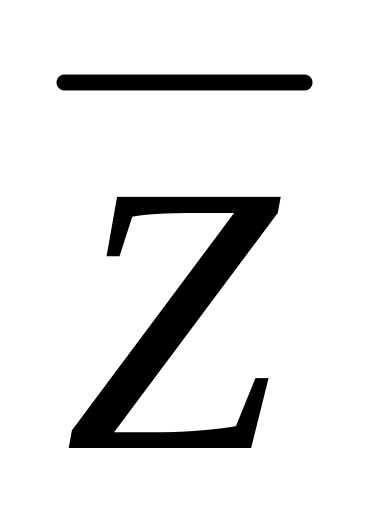
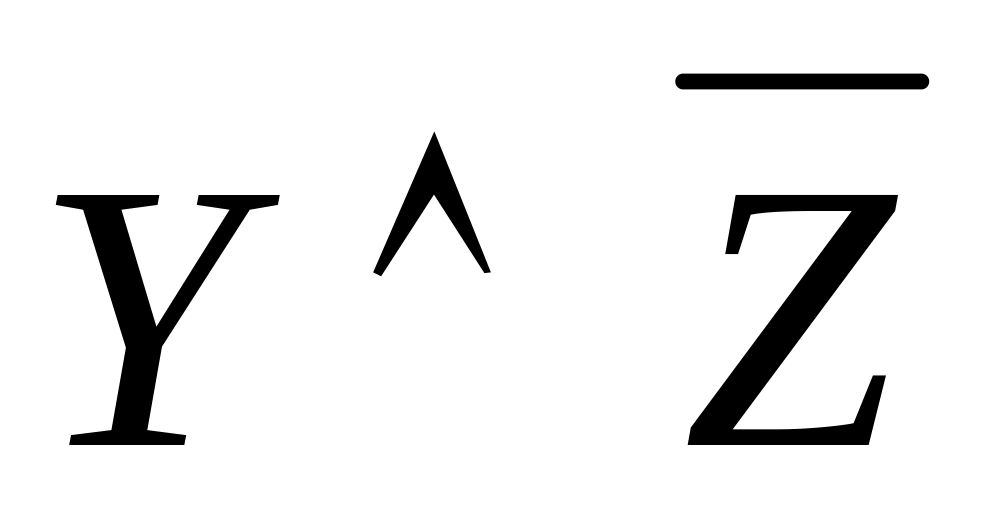
0
0
0
1
1
0
1
0
0
1
1
0
0
1
0
1
0
1
1
1
1
0
1
1
1
0
0
1
1
0
0
0
1
0
1
1
0
1
0
0
0
1
1
1
0
0
1
1
0
1
1
1
0
0
0
1
Задача 5. Доказать равносильность, используя основные законы логических операций:
.
Решение.
1.Используя законы де Моргана и , получим:
.
2.Используя
закон двойного отрицания
,
получаем:
.
3. Применяя
распределительный закон
,
получаем
=
=
.
4. Ассоциативность дизъюнкции позволяет упростить последнее выражение:
.
5. Учитывая законы, включающие тождественно ложные высказывания, окончательно получаем:
.
Задача 6. С
помощью таблиц истинности проверить,
являются ли эквивалентными высказывания:
и
.
Решение.
Таблица 17.
X |
Y |
Z |
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
Так как значения для высказываний и в таблице истинности не совпали, то они не эквивалентны.
Задача 7. Определите для высказывания, будет ли оно логически истинным, противоречивым; ни тем, ни другим.
.
Решение.
По прежнему, составляем таблицу истинности для высказывания
Таблица 18.
-
X
Y
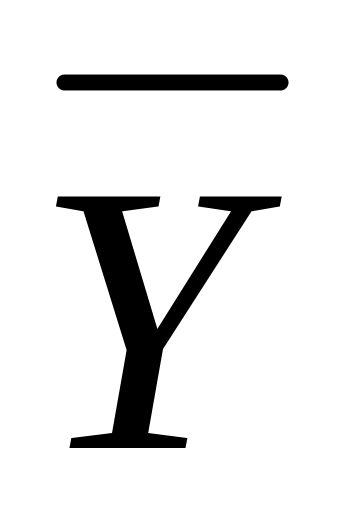
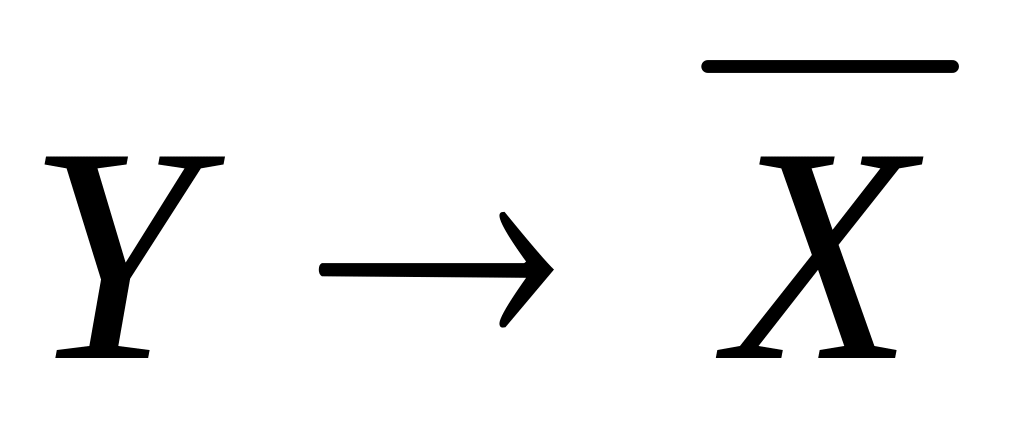
0
0
1
1
1
1
0
1
0
1
1
1
1
0
1
1
1
1
1
1
0
0
0
1
(т)
– логически истинное высказывание.
Задача 8.
Постройте таблицы истинности следующих
составных высказываний: (а)
;
(б)
;
(в)
;
(г)
;
(д)
.
Для каких пар имеет место отношение
следствия или эквивалентности?
Ответ: (б) эквивалентно (в), из (а) следует (г), из (д) следует (б), (в).
Задача 9.
Постройте составные высказывания,
эквивалентные а)
;
б)
,
используя только связки отрицания и
конъюнкции.
Задача 10.
Если Х и Y логически истинны,
а Z - логически ложно, что можно
сказать о высказывании
?
Ответ: логически истинно.
Задача 11. Пусть Х означает: «Я сдам экзамен»; а Y: «Я буду регулярно выполнять домашние задания». Запишите в символической форме следующие высказывания:
(а) « Я сдам этот экзамен только в том случае, если буду регулярно выполнять домашние задания».
(б) «Регулярное выполнение домашних заданий является необходимым условием для того, что я сдам этот экзамен».
(в) «Сдача этого экзамена является достаточным условием того, что я регулярно выполнял домашние задания».
(г) «Я сдам этот экзамен в том и только в том случае, если я буду регулярно выполнять домашние задания».
(д) «Регулярное выполнение домашних заданий есть необходимое и достаточное условие того, чтобы я сдал экзамен».
Выясните,
какому из перечисленных высказываний
соответствуют следующие символические
формы:
.
Задача 12.
Докажите равносильность
с помощью формул алгебры высказываний.
Решение.
Используя формулу
,
запишем:
,
тогда
по
закону де Моргана, т.е.
,
т.к. по закону двойного отрицания
,
что и требовалось доказать.
Полученная формула дает правило
построения отрицания для импликации,
часто применяемое в математических
рассуждениях:
.
Задача 13. Проверьте, будут ли эквивалентны следующие формулы:
а)
и
б)
и
.
Решение. Составим таблицы истинности:
Таблица 19.
X |
У |
Z |
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
Формулы не эквивалентны.
Таблица 20.
X |
У |
Z |
|
|
|
|
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
Формулы эквивалентны.
Задача 14. Постройте таблицы истинности для высказываний:
а)
;
б)
.
Какие другие составные высказывания имеют те же таблицы истинности? Покажите, что любая таблица истинности может быть реализована посредством составного высказывания, в котором используется единственная связка: стрелка Пирса.
Задача 15. Докажите, что импликация
эквивалентна
.
Решение. Доказательство проведем с помощью таблицы истинности.
Таблица 21.
-
X
У
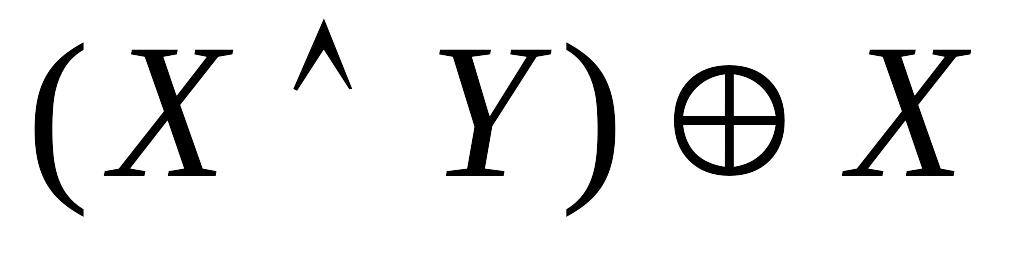
1
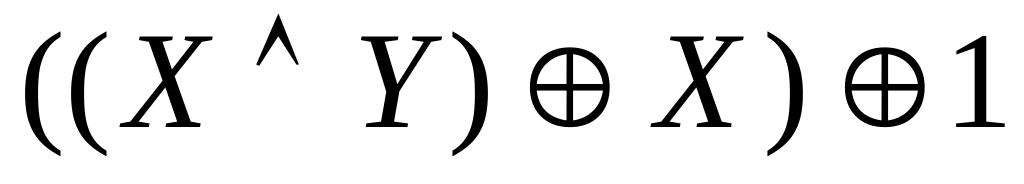
0
0
1
0
0
1
1
0
1
1
0
0
1
1
1
0
0
0
1
1
0
1
1
1
1
0
1
1
Одинаковость третьего и седьмого столбцов и является доказательством в задаче.