Учебное пособие 1874

Решение. Находим по формулам (1.7.4):

Упражнения:

1.Найти н.о.д. чисел: а) 48 и 54; б) 245, 105 и 441.

2.Найти н.о.к. чисел: а) 90 и 120; б) 363, 440 и 198.

3.Доказать, что н.о.к. нескольких чисел делится на их н.о.д.

4.Показать, что если (a, b) = k, то (a/k, b/k) = l.

5.Чему равны целые и дробные части чисел:

D(– 7 3 ), E ( 3 ), F (– 5 ).

Ук а з а н и е. Отрезок длиной 3 можно найти как гипотенузу прямо-

угольного треугольника с катетами 1 и 2 (построение отрезка длиной 2 рассматривалось в тексте).

14.Построить на плоскости точки А(–3, –4), В (0, 5), С (5, 0), D(-2, 6), E(3, 3), F(–4, 3), G(–6, 6), H (6, -6).

15.Дана точка A (2, –3). Указать координаты точек, симметричных с А относительно оси Ох, оси Оу, начала координат, биссектрисы I – III координатных углов.

67

16.Показать, что точки А (х, у) и В( –у, –х) симметричны относительно биссектрисы II – IV координатных углов.

17.Построить точки по их полярным координатам: А (2, 5π/6), B(1, π),

С(3, 0), D( 2 , –π/4). Найти декартовы координаты этих точек.

18. Найти полярные координаты точек (заданных декартовыми координа-

тами) A (2, 0), B(–1, 0), С (0, 2), D(–1, –1).

1.8. Степени с натуральными показателями. Пусть а – произвольное действительное число, а п – натуральное число. Произведение

a a a ...a

n

п сомножителей, равных а, называется п-й степенью числа а и обозначается через аn. При этом а называется основанием, a n – показателем степени. При n = 1 просто полагают a1 = а. Таким образом, степень аn определяется при любых натуральных значениях п. Поскольку действие возведения в натуральную степень определено через действие умножения, то оно рассматривается как рациональное (арифметическое) действие. Отметим некоторые свойства этого действия.

1) При любых натуральных п, т

Таким образом, при умножении степеней с одинаковыми основаниями показатели степени складываются.

2) Если n > m и а 0, то

68

Доказательство свойств 4) и 5) предоставляется читателю.

1.9. Степени с целыми показателями. Свойство 2) п. 1.8:

установлено при п > т. При п=т или п < т его правая часть не определена, но левая часть сохраняет смысл. Это дает повод ввести определение степени с нулевым и целыми отрицательными показателями степени.

Нулевую степень числа a 0 полагают по определению равной единице:

Таким образом, равенство (1.8.2) становится теперь верным и при п = т. Степень числа a 0 с отрицательным показателем –k определяется

равенством

Нулевая и отрицательная степени числа 0 не определяются.

Определение (1.9.2) делает равенство (1.8.2) верным и при п < т. Так, если m = n + k, то имеем

Нетрудно проверить, что все правила действия возведения в натуральную степень, указанные в п. 9, сохраняют силу при введенных определениях и при любых целых показателях степени.

Так, например, проверяем, что

т. е. и для отрицательных показателей степени сохраняет силу правило 1) умножения степеней с одинаковыми основаниями.

Пример. Вычислить: 2 3 35 64 .

2 39 6 2

Решение. Используем то, что 6= 2 3, и применяем правила действий с целыми степенями:

1.10. Корни. Если п > 1 – натуральное число, а а и b – действительные числа, причем

bn a

69

то число b называется корнем n-й степени из числа а. Таким образом, корнем п-й степени из числа а называется каждое число b такое, что его n-я степень равна а.

Действие отыскания корня из числа а называется действием извлечения корня n-й степени из а. Действие извлечения корня степени п является действием, обратным по отношению к действию возведения числа в степень n.

Если n – нечетное число, то, как можно доказать, для любого действительного числа а существует единственное значение корня степени п (в действительной области).

Если п – четное, то действие извлечения корня степени n из отрицательного числа невозможно, так как четная степень любого числа неотрицательна. Можно показать, что для любого положительного числа а корень четной степени n имеет два значения, равных по абсолютной величине и противоположных по знаку. Например, числа +3, —3 суть корни квадратные из числа 9. Положительный корень четной степени из положительного числа называется арифметическим корнем (или арифметическим значением корня).

Его единственность видна из такого соображения. Если бы имелось два положительных корня b1 и b2, то одно из чисел b1, b2 было бы больше другого, например, b1 > b2. Но тогда и b12 > b22, т. е. оба числа не могли бы быть корнями степени п из одного и того же числа а. Это рассуждение применимо и к случаю корней нечетной степени.

Наметим обоснование утверждения о существовании корня na произвольной степени из любого положительного действительного числа. Прежде всего, может случиться, что корень существует в области натуральных чисел. Если это так, то этим задача решается; если в области натуральных чисел корня не имеется, то найдутся два последовательных целых числа k и k+1 такие, что kn < а, (k+1)n > а. Теперь будем рассматривать десятичные дроби вида k.a1, где a1 = 0, 1, ..., 9. Либо среди них имеется искомый корень, либо снова получим для некоторого a1

Далее будем искать приближение корня в виде дроби с двумя знаками после запятой и т. д. Таким путем в принципе можно построить ряд десятичных приближений по недостатку и по избытку для некоторого действительного числа, которое и следует принять за значение искомого корня (аналогично

примеру 2 в п. 6).

Корень степени n обозначается с помощью знака радикала n ; при этом

для придания символу na вполне определенного смысла условимся понимать под na :

1)единственное значение корня в случае нечетного n (а в этом случае – любое действительное число).

2)арифметический корень степени n из а в случае четного п (в этом случае а > 0).

Корень из нуля при любом показателе n равен нулю.

70

В случае, если мы хотим рассматривать оба значения корня четной

степени из положительного числа, то пишем ± na ; если перед корнем четной степени знак не написан, то всегда имеют в виду арифметическое значение корня.

В случае корня степени 2 (квадратного корня) пишут просто na ;

например, 9 = 3. Корень третьей степени называют кубическим корнем. Если а – произвольное действительное число, то

na n a

при нечетном n и

nan a

при четном n (в частности, в случае квадратного корня). Так, например,

Укажем основные правила действий над корнями; для простоты предположим, что числа под знаком корня – положительные.

1) Извлечение корня из произведения. Корень из произведения равен произведению корней из сомножителей:

Доказательство. Для доказательства этого (и дальнейших) свойства достаточно проверить, что при возведении обеих частей равенства (1.10.1) в степень т получим одно и то же число. При этом мы пользуемся соотношением

откуда и вытекает требуемое свойство.

2) Возведение корня в степень. Для возведения корня в степень достаточно возвести в эту степень подкоренное выражение, сохраняя показатель корня.

Это правило записывается так:

ma k mak .

Свойство 2) непосредственно вытекает из свойства 1), а также может быть проверено возведением обеих частей равенства (10.2) в степень т.

3) Извлечение корня из частного. Корень из частного равен частному от деления корня из числителя на корень из знаменателя:

71

4) Извлечение корня из степени. Пусть показатель степени т является кратным показателя корня п: m = nk. Тогда

т. е. при извлечении корня из степени показатель степени следует разделить на показатель корня.

Пусть в общем случае т не является кратным п; выполним деление т на

равен k (п. 3). Это значит, что m = kr и n = ks, причем r и s – целые взаимно

простые числа. Тогда ma n = r a s . Это означает, что если показатели корня и подкоренного выражения имеют общий делитель, то на него их можно

7) Приведение корней к общему показателю. Пользуясь только что установленным свойством, можно два или несколько корней приводить к общему показателю, который представляет собой н. о. к. показателей всех данных корней.

Это преобразование полезно применять при умножении корней с разными показателями.

Пример 2. Упростить произведение 2 34 62 .

Решение. 234 62 623 642 62 6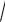28 324 232 . Здесь н. о. к.

показателей корней равнялось 6; в процессе преобразования мы применили также правило 6) сокращения показателей степени и корня и правило 1). Аналогичным образом выполняется и деление корней.

1.11. Степени с рациональными показателями. Степени с дей-

ствительными показателями. Будем, как и в п. 10, рассматривать только корни из положительных чисел. Мы видели, что в случае, когда т делится нацело на п,

na m a mn .

72

Обобщая это правило, можно ввести следующее определение степени с положительным рациональным показателем p/q:

В случае отрицательного рационального показателя степени – p/q полагают (по аналогии со случаем целого отрицательного показателя степени)

На степени с рациональными показателями распространяются все правила действий над степенями с натуральными и вообще целыми показателями. Для их обоснования достаточно применить правила п. 1.11 действий над корнями. Докажем, например, свойство

a p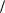q a pq a pq pq .

Имеем

a pq qa p qqa pp.

Рассматривают также степени положительного числа а при произвольных действительных показателях. В основу определения ax при иррациональном х кладется последовательное приближение х рациональными числами. Так,

По мере продолжения этого процесса левая и правая части неравенств, выраженные бесконечными десятичными дробями, будут иметь все большее и большее число совпадающих десятичных знаков, которые и будут приниматься

за десятичные знаки, определяющие иррациональное число 32 . Более подробно рассматривать этот вопрос мы не можем, но отметим, что аx имеет действительное вполне определенное значение при а > 0 и любом действительном х.

73

Замечание. Извлечение корня нечетной степени возможно и из отрицательного числа. Поэтому выражению аp/q при а < 0 также можно

приписать смысл с помощью равенства аp/q = qa p в случае, когда несократимая рациональная дробь p/q имеет нечетный знаменатель. В случае четного q и для иррациональных значений показателя степень отрицательного основания не определяется. Нуль в любой положительной степени равен нулю; нулевая и отрицательные степени нуля не определены.

Пример. Произвести действия, пользуясь отрицательными и дробными показателями степени: 5 89

2.ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ

2.1.Формулы сокращенного умножения. В некоторых часто встречающихся случаях применяют формулы сокращенного умножения двух многочленов. Напомним эти формулы.

а) Квадрат суммы и квадрат разности. Квадрат двучлена (бинома) а+b

можно записать в виде

(a+b)2 = (a+b)(a+b).

На основании правила умножения многочленов можно раскрыть стоящие справа скобки, а именно каждый член первого бинома умножить на каждый член второго бинома и результаты сложить. Получим

Формулу (2.1.1) иногда записывают в виде

Формула (2.1.2) для квадрата двучлена (бинома) распространяется на случай, когда в квадрат возводится любой многочлен (полином). Покажем это для случая трехчлена. Имеем

(a+b+c)2 = [(a+b)+c]2 = (a+b)2 + c2 + 2(a+b)c =

74

Вообще, квадрат алгебраической суммы нескольких слагаемых равен сумме квадратов этих слагаемых плюс сумма удвоенных попарных произведений этих слагаемых (с учетом правила знаков!).

Пример. Раскрыть скобки в выражении (2—Зх—5х2 - х3)2.

Решение. Имеем

После приведения подобных членов запишем ответ:

2 3x 5x2 x3 2 4 12x 11x2 34x3 19x4 10x5 x6 .

б) Куб суммы и куб разности. Чтобы вывести формулу для (a+b)3 заметим, что

(a + b)3 = (a + b)(a + b)2.

Но выражение для (а + b)2 уже найдено – (1.2); поэтому

(а + b)3 = (а2 + b2 + 2ab) (а + b).

Перемножая почленно многочлены, стоящие в правой части этого

равенства, получим

(a + b)3 = а3 + b2a + 2a2b + 2ab2 + a2b + b.

Последний результат можно переписать так:

в) Разность квадратов. Следующая формула:

легко проверяется умножением двучленов в ее левой части.

г) Сумма и разность кубов. Также рекомендуется проверить самостоятельно следующие формулы:

Трехчлены (a2 – ab + b2) и (a2 + ab + b2) в левых частях равенств (2.1.11), (2.1.12) часто называют ―неполным квадратом‖ разности или суммы соответственно.

2.2. Разложение многочлена на множители. В некоторых случаях данный многочлен может быть представлен как произведение одночлена на многочлен или как произведение двух многочленов. В первом случае говорят, что за знак скобок можно вынести общий множитель, во втором, – что многочлен разлагается на множители. Нам известны некоторые приемы разложения многочлена на множители, в том числе метод группировки и применение формул сокращенного умножения. Ограничимся разбором нескольких типичных примеров (общего универсального метода, чтобы узнать, разлагается ли многочлен на множители и найти их, не имеется).

Пример 1. Разложить на множители x2 2xy 2 yz z 2 .

75

Решение. Производим группировку слагаемых:

Мы применили здесь формулу разности квадратов (2.1.10) и прием вынесения общего множителя за скобку.

Пример 2. Разложить на множители:

б) Добавим к нашему выражению и вычтем выражение Заb(а + b), чтобы получить куб суммы по формуле (2.1.8):

В некоторых случаях разложение на множители не удается в действительной области, но может быть осуществлено в комплексной области.

Так, например, a2 b2 нельзя разложить на действительные множители, но

но она же разлагается и на действительные множители:

a2 b2 ab2 a2 b2 ab 2 .

2.3. Дробные алгебраические выражения. Алгебраическое выражение в записи которого наряду с действиями сложения, вычитания и умножения используют также деление на буквенные выражения, называется дробным алгебраическим выражением. Таковы, например, выражения

Алгебраической дробью мы называем алгебраическое выражение, имеющее вид частного от деления двух целых алгебраических выражений (например, одночленов или многочленов). Таковы, например, выражения

76