Учебное пособие 1874

Пусть даны два натуральных числа а и b < а. Произведем деление а на b; если а разделится на b нацело, то b – н.о.д. чисел a, b. В противном случае

Теперь будем делить b на r1; если b разделится на r1 нацело, то r1 окажется общим делителем чисел a и b; действительно, в этом случае оба слагаемых правой части равенства (1.4.2) делятся на r1 нацело, значит, делится на r1 нацело и его левая часть a. То, что r1 явится именно наибольшим общим делителем a и b, также видно из (1.4.2): если d – какой-нибудь общий делитель чисел a, b, то он будет также делителем числа r2.

Если b делится на r1 с остатком, то придем к равенству вида

осуществится первая из этих возможностей, то r2 будет н.о.д. чисел а и b (это легко доказать, пользуясь равенствами (1.4.2), (1.4.3); рекомендуем читателю провести это доказательство). Если же осуществляется вторая возможность, то получим результат деления

r1 = r2q2 + r3, r3 < r2,

и вновь будем делить r2 на r3. Процесс обязательно закончится на некотором шаге; числа b, r1, r2, ... последовательно уменьшаются, и либо одно из них, не равное единице, окажется делителем предыдущего (оно и будет н.о.д. чисел а, b), либо цепочка чисел b > r1 > r2 > ... закончится единицей. В этом случае н.о.д. чисел а, b равен единице, числа а, b взаимно простые.

Пример. Найти н.о.д. чисел 162 и 42, пользуясь алгоритмом Евклида.

Решение. Делим 162 на 42:

162 = 42 3 + 36.

Остаток r1 = 36; делим b = 42 на r1 = 36:

42 = 36 1 + 6.

Второй остаток r2 = 6. Делим r1 = 36 на r2 = 6: 36 = 6 6.

Деление выполняется без остатка; поэтому r2 = 6 – н.о.д. чисел 162 и 42.

1.5. Десятичные дроби. Представление рациональных чисел десятичными дробями. Десятичной дробью называется дробь, у которой знаменатель представляет собой натуральную степень числа 10. Такой,

например, является дробь 7823436 . Эту дробь можно записать в следующей

10000

форме: выписать в строку цифры числителя и отделить запятой справа столько из них, сколько нулей содержится в знаменателе, а именно:

7823436 782,3436 .

10000

В такой записи цифры, стоящие слева от запятой, образуют целую часть,

ацифры, стоящие справа от запятой, – дробную часть данной десятичной дроби. Пусть p/q – какое-либо положительное рациональное число. Из

арифметики хорошо известен процесс деления, позволяющий представлять число p/q в виде десятичной дроби. Сущность процесса деления состоит в том,

57

что сначала находят, какое наибольшее целое число раз q содержится в p; если p – кратное q, то на этом процесс деления и заканчивается. В противном случае, появляется остаток. Далее находят, сколько в этом остатке содержится десятых долей q, и на этом шаге процесс может закончиться, либо появится новый остаток. В последнем случае находят, сколько в нем содержится сотых долей q, и т. д.

Если знаменатель q не имеет никаких других простых делителей, кроме 2 или 5, то через конечное число шагов остаток окажется равным нулю, процесс деления закончится и данная обыкновенная дробь обратится в конечную десятичную дробь. В самом деле, в указанном случае всегда можно подобрать такое целое число, что после умножения на него числителя и знаменателя данной дроби получится равная ей дробь, у которой знаменатель будет представлять натуральную степень десяти. Такой, например, является дробь

Однако, не производя этих преобразований, разделив числитель на знаменатель, читатель получит тот же результат: 59/40 = 1,475.

Если знаменатель несократимой дроби имеет по меньшей мере один простой делитель, отличный от 2 или 5, то процесс деления р на q не закончится никогда (никакой из очередных остатков в нуль не обратится).

Выполнив деление, найдем

965 7,310606 ...

132

Для записи результата, получаемого в этом примере, периодически повторяющиеся цифры 0 и 6 заключают в круглые скобки и пишут:

В этом примере и в других подобных случаях действие деления не приводит к окончательному результату в виде десятичной дроби. Можно, обобщая понятие десятичной дроби, все же говорить, что частное 965/132 представлено бесконечной периодической дробью 7,31(06). Повторяющиеся цифры 06 называют периодом этой дроби, а их число, равное в нашем примере 2, – длиной периода.

Чтобы уяснить причину явления периодичности дроби, разберем, например, процесс деления на 7. Если деление нацело не выполняется, то появляется остаток, который может иметь только одно из следующих значений: 1, 2, 3, 4, 5, 6. И на каждом из следующих шагов остаток будет иметь снова одно из этих шести значений. Поэтому не позднее чем на седьмом шаге, мы неизбежно встретимся с одним из значений остатка, которые раньше уже появлялись,

58

Начиная с этого места, процесс деления приобретет периодический характер. Периодически будут повторяться и значения остатков, и цифры частного. Такое рассуждение применило и в случае любого другого делителя.

Таким образом, всякая обыкновенная дробь p/q представляется конечной или бесконечной периодической десятичной дробью. Замечательно, что и, обратно, всякая периодическая десятичная дробь представима в виде обыкновенной дроби. Покажем, как выполняется это действие. При этом используется формула суммы бесконечно убывающей геометрической прогрессии.

Запись

здесь члены правой части, начиная со второго, образуют бесконечную. геометрическую прогрессию со знаменателем l/102 = 0,01 и первым членом 6/104 = 0,0006. Пользуясь формулой:

Ясно, что этот же процесс позволит любую заданную бесконечную периодическую дробь представить в виде обыкновенной дроби (и, как можно показать, именно той, из которой в процессе деления в свою очередь получается данная бесконечная периодическая дробь). Впрочем, здесь имеется одно исключение. Рассмотрим дробь 0,4999...= 0,4(9) и применим к ней процесс преобразования в обыкновенную дробь:

– мы пришли к числу 1/2, которое представляется конечной десятичной дробью

12 = 0,5.

Сходный результат получится всякий раз, когда период данной бесконечной дроби имеет вид (9). Поэтому мы отождествляем такие пары чисел, как, например,

и т. д.

Иногда полезно еще допускать записи вида

0, 5 = 0, 5000 … = 0, 5(0),

59

представляя формально конечные десятичные дроби как бесконечные с периодом (0).

Все сказанное об обращении обыкновенной дроби в десятичную периодическую дробь и обратно относилось к положительным рациональным числам. В случае отрицательного числа можно поступить двояким образом.

1) Взять положительное число, противоположное данному отрицательному, обратить его в десятичную дробь, а затем поставить перед ней знак минус. Например, для -5/3 получим

2) Данное отрицательное рациональное число представить в виде суммы его целой части (отрицательной) и его дробной части (неотрицательной), а затем обратить в десятичную дробь только эту дробную часть числа. Например:

Для записи чисел, представленных в виде суммы своей отрицательной целой части и конечной или бесконечной десятичной дроби, принято такое обозначение (искусственная форма записи отрицательного числа):

2 0, 3 2, 3 ,

1 0,25 1,25.

Здесь знак минус ставится не перед всей дробью, а над ее целой частью, чтобы подчеркнуть, что только целая часть отрицательна, а следующая за запятой дробная часть положительна.

Такая запись создает единообразие в записи положительных и отрицательных десятичных дробей и будет использована в будущем в теории десятичных логарифмов. Предлагаем читателю для практики проверить переход от одной записи к другой в примерах:

Теперь уже можно сформулировать окончательный вывод:

всякое рациональное число может быть представлено бесконечной десятичной периодической дробью, и, обратно, всякая такая дробь задает рациональное число. Конечная десятичная дробь допускает также две формы записи в виде бесконечной десятичной дроби: с периодом (0) и с периодом (9).

1.6. Иррациональные числа. Действительные числа. Не все действия,

рассматриваемые в алгебре, выполнимы в поле рациональных чисел. Примером может служить операция извлечения квадратного корня. Так, если равенство x2 = 4 выполняется при значениях x = 2, x = -2, то равенство x2 = 2 не имеет места ни при каком рациональном значении х. Докажем это. Сначала заметим, что целое х не может иметь квадрата, равного 2: при x = 1 имеем x2 = 1, а при х

60

> 1 x2 заведомо больше 2. Предположим теперь, что х дробное: x = p/q (дробь считается несократимой) и (p/q)2 = 2.

Отсюда имеем p2 = 2q2; p должно быть четным числом (иначе квадрат р не был бы четным). Положим p=2k, p2 = 4q2. Теперь 4k2 = 2q2, q2 = 2k2; получается, что и q—четное, что противоречит допущению о не сократимости дроби p/q.

Это показывает, что в области рациональных чисел из числа 2 нельзя

извлечь квадратный корень, символ 2 не имеет смысла в области рациональных чисел. Между тем задача: ―найти сторону х квадрата, зная, что площадь его равна S‖ – столь же естественна при 5 = 2, как и при 5 = 4. Выход из этого и других подобных затруднений состоит в дальнейшем расширении понятия числа, во введении нового вида чисел— иррациональных чисел.

Покажем, как вводятся иррациональные числа на примере задачи извлечения квадратного корня из числа 2; для простоты ограничимся положительным значением корня.

Для каждого положительного рационального числа х будет иметь место одно из неравенств х2 < 2 или х2 > 2. Очевидно, что 12 < 2, 22 > 2. Рассматриваем затем числа 1,0; 1,1; 1,2; ..., 1,9; 2,0 и находим два соседних среди них с тем свойством, что первое имеет квадрат, меньший двух, а второе – больший двух. Именно, l,42 < 2 и l,52 > 2. Аналогично, продолжая этот процесс, получим ряд неравенств (для получения десятичных дробей, написанных здесь, можно также использовать известный алгоритм приближенного извлечения квадратного

корня):

12 < 2 < 22,

l,42 < 2 < l,52,

l,412 < 2 < l,422, l,4142 < 2 < 1,4152, l,41422 < 2 < 1,41432,

l,414212 < 2 < 1,414222, 1,4142132 < 2 < 1,4142142, 1,41421352 < 2 < 1,4142136,

Сопоставляя сначала целые части, а затем первые, вторые, третьи и т. д. цифры после запятой у рациональных чисел, между квадратами которых лежит 2, мы можем последовательно выписать эти десятичные знаки:

может быть продолжен неограниченно. Поэтому можно рассматривать дробь (1.6.1) как бесконечную десятичную дробь (непериодическую, так как в случае периодичности она представляла бы рациональное число). Эта бесконечная непериодическая дробь, любое число десятичных знаков которой мы можем выписать, но для которой нельзя осуществить записи одновременно всех

знаков, и принимается за число, равное 2 (т. е. за число, квадрат которого равен 2).

61

Отрицательное значение корня квадратного из двух мы представим в

виде

2 1, 4142135...

или, пользуясь искусственной формой записи чисел, в виде

2 2,5857864...

Введем теперь следующее определение: иррациональным числом называется всякая бесконечная непериодическая десятичная дробь

a = a1a2a3 … an …

где а – целая часть числа (она может быть положительной, равной нулю или отрицательной), а1, a2, ... an – десятичные знаки (цифры) его дробной части.

Заданное бесконечной непериодической дробью иррациональное число определяет две последовательности конечных десятичных дробей, называемых

десятичными приближениями а по недостатку и по избытку:

Например, для a = 2 запишем

и т. д. Здесь, например, 1,41 – десятичное приближение 2 с точностью до 0,01 по недостатку, а 1,42 – по избытку.

Запись неравенств между иррациональным числом и его десятичными приближениями входит в самое определение понятия иррационального числа и может быть положена в основу определения соотношений «больше» и «меньше» для иррациональных чисел.

1.7. Числовая ось. Координаты точки на плоскости. Осью называется прямая, на которой одно из двух возможных направлений выделено как положительное (противоположное направление считается отрицательным). Положительное направление обозначается обычно стрелкой. Числовой (или координатной) осью называется ось, на которой выбрана начальная точка (или начало) О и единица масштаба или масштабный отрезок ОЕ (рис. 1). Таким

Рис. 1.

С помощью точек числовой оси изображают действительные числа Целые числа изображаются точками, которые получаются откладыванием масштабного отрезка нужное число раз вправо от начала О в случае положительного целого числа и влево в случае отрицательного. Нуль изображается начальной точкой О (сама буква О

62

напоминает о нуле; она является первой буквой слова origo, означающего «начало»). Дробные (рациональные) числа также просто изображаются точками

следует отложить влево от О три масштабных отрезка и еще одну третью часть масштабного отрезка (точка А на рис. 1). Кроме точки А на рис. 1 показаны еще точки В, С, D, изображающие соответственно числа – 2, 3 2 , 4.

Целых чисел имеется бесконечное множество, но на числовой оси целые числа изображаются точками, расположенными ―редко‖, целочисленные точки оси отстоят от соседних на единицу масштаба. Рациональные точки расположены на оси весьма ―густо‖ – нетрудно показать, что на любом сколь угодно малом участке оси имеется бесконечно много точек, изображающих рациональные числа Тем не менее на числовой оси имеются точки, которые не являются изображениями рациональных чисел. Так, если на числовой оси построить отрезок О А, равный гипотенузе ОС прямоугольного треугольника ОЕС с катетами ОЕ = ЕС = 1 (рис. 2), то длина этого отрезка (по теореме

Пифагора) окажется равной 2 и точка А не будет изображением рационального числа.

Исторически именно факт существования отрезков, длины которых не могут быть выражены числом (рациональным числом!), привел к введению иррациональных чисел.

Введение иррациональных чисел, которые в совокупности с рациональными образуют множество всех действительных чисел, приводит к тому, что каждой точке числовой оси соответствует единственное действительное число, изображением которого она служит. Напротив, каждое действительное число изображается вполне определенной точкой числовой оси.

Между действительными числами и точками числовой оси устанавливается взаимно однозначное соответствие.

Поскольку мы числовую ось мыслим как непрерывную линию, а точки ее находятся во взаимно однозначном соответствии с действительными числами, то мы говорим о свойстве непрерывности множества действительных чисел.

Заметим еще, что в некотором смысле иррациональных чисел несравненно больше, чем рациональных.

Число, изображением которого служит данная точка А числовой оси, называется координатой этой точки, тот факт, что а – координата точки А, записывают так: А (а). Координата любой точки А выражается как отношение ОА/ОЕ отрезка ОА к масштабному отрезку ОЕ, которому для точек, лежащих от начала О в отрицательном

направлении, приписывают знак минус.

Введем теперь прямоугольные декартовы координаты на плоскости. Возьмем две взаимно перпендикулярные числовые оси Ох и Оу, имеющие общее начало О и равные масштабные отрезки (на практике часто применяют и

63

координатные оси с различными масштабными единицами) Скажем, что эти оси (рис. 3) образуют декартову прямоугольную систему координат на плоскости. Точка О называется началом координат, оси Ох и Оу – осями координат (ось Ох называют осью абсцисс, ось Оу – осью ординат). На рис. 3,

как обычно, ось абсцисс расположена горизонтально, ось ординат – вертикально. Плоскость, на которой задана система координат, называют

координатной плоскостью.

Каждой точке плоскости ставится в соответствие пара чисел – координат этой точки относительно данной координатной системы. Именно, возьмем прямоугольные проекции точки М на оси Ох и Оу, соответствующие точки на осях Ох, Оу обозначены на рис. 3 через Мx, My. Точка Мx имеет, как точка числовой оси Ох, координату (абсциссу) х, точка My, как точка числовой оси Оу, – координату (ординату) у. Эти два числа х, у (записанные в указанном порядке)

и называются координатами точки М.

При этом пишут: М (х, у}.

Итак, каждой точке плоскости ставится в соответствие упорядоченная пара действительных чисел (х, у)—декартовы прямоугольные координаты этой точки. Термин ―упорядоченная пара‖ указывает на то, что следует различать первое число пары – абсциссу и второе – ординату. Напротив, каждая пара чисел (х, у) определяет единственную точку М, для которой х служит абсциссой, а у – ординатой. Задание в плоскости прямоугольной декартовой системы, координат устанавливает взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел.

Координатные оси делят координатную плоскость на четыре части, четыре квадранта. Квадранты нумеруются, как показано на рис. 3, римскими

цифрами.

Знаки координат точки зависят от того, в каком квадранте она лежит, как указано в следующей таблице:

Точки, лежащие на оси Ох, имеют ординату у, равную нулю, точки на оси Оу—абсциссу х, равную нулю. Обе координаты начала О равны нулю:О(0, 0).

Пример 1. Построить на плоскости точки

A (6,0), В (2, 7), С (0, 4), D(-5,2), E(-3,0), F(-4, -9), G(0,-3), H(3,-8).

Решение дается на рис. 4.

Если известны координаты некоторой точки М (х, у), то легко указать координаты точек, симметричных с ней относительно осей Ох, Оу и начала

64

координат: точка, симметричная с М относительно оси Ох, будет иметь координаты (х, –у); точка, симметричная с М относительно Оу, – координаты (– x, y); наконец, у точки, симметричной с М относительно начала, координаты будут

(—х, —у).

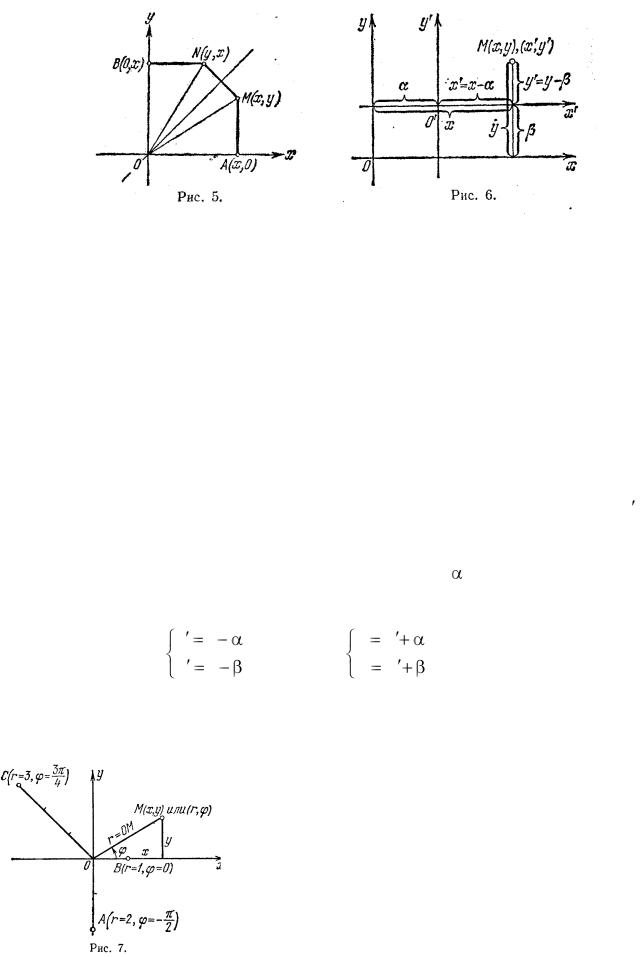
Можно также указать связь между координатами пары точек, симметричных относительно биссектрисы I – III координатных углов (рис. 5); если одна из этих точек М имеет координаты х и у, то у второй абсцисса равна ординате первой точки, а ордината – абсциссе первой точки. Иначе говоря, координаты точки 'N, симметричной с М относительно биссектрисы I – III координатных углов, будут (у, х). Для доказательства этого положения рассмотрим прямоугольные треугольники ОАМ и OBN. Они расположены симметрично относительно биссектрисы координатного угла и потому равны. Сравнивая их соответственные катеты, убедимся в правильности нашего утверждения.

Систему декартовых прямоугольных координат можно преобразовать с помощью переноса ее начала О в новую точку O без изменения направления осей и величины масштабного отрезка. На рис. 6 показаны одновременно две системы координат: ―старая‖ с началом О и ―новая‖ с началом O . Произвольная точка М имеет теперь две пары координат, одну относительно старой координатной системы, другую относительно новой. Если координаты нового начала в старой системе обозначены через ( , β), то связь между старыми координатами (х, у) точки М и ее новыми координатами (х', у') выразится формулами

Эти формулы называют формулами переноса системы координат; при их выводе по рис. 6 выбрано самое удобное положение точки М, лежащей в первом квадранте как старой, так и новой системы. Можно убедиться, что формулы (1.7.1) остаются верны при любом

расположении точки М.

Положение точки М на плоскости может быть задано не только ее декартовыми прямоугольными координатами х, у, но и

65

другими способами. Соединим, например, точку М с началом О (рис. 7) и рассмотрим следующие два числа: длину отрезка ОМ — r и угол наклона этого отрезка к положительному направлению оси Ох (этот угол определяется как угол, на который надо повернуть F ось Ох до ее совмещения с ОМ, и считается положительным, если поворот совершается против часовой стрелки, и отрицательным в противном случае, как это принято в тригонометрии. Отрезок r = ОМ называется полярным радиусом точки М, угол ( – ее полярным углом, пара чисел (r, ) – полярными координатами точки М. Как видно, для определения полярных координат точки требуется задание только одной координатной оси Ох (называемой в этом случае полярной ось/о). Удобно, однако, рассматривать одновременно и полярные и декартовы прямоугольные координаты, как это сделано на рис. 7.

Полярный угол точки определяется заданием точки неоднозначно: если 0 один из полярных углов точки, то и всякий угол

будет ее полярным углом. Задание полярного радиуса и угла определяет положение точки единственным образом. Начало О (называемое полюсом полярной системы координат) имеет радиус, равный нулю, никакого определенного полярного угла точке О не приписывается.

Между декартовыми и полярными координатами точки имеются следующие соотношения:

непосредственно вытекающие из определения тригонометрических функций. Эти соотношения позволяют находить декартовы координаты по заданным полярным. Следующие формулы:

позволяют решать обратную задачу: по данным декартовым координатам точки

66