Электричество и магнетизм. лабораторный практикум. Белко В.Н., Никишина А.И

УДК 53.07 ББК 22.2:22. я7

Б 433

Рецензенты:

кафедра материаловедения и физики металлов Воронежского государственного технического университета; С.Б. Кущев, профессор Воронежского государственного технического университета

Белко, В.Н.

Б 433 Электричество и магнетизм: лабораторный практикум / В.Н. Белко, А.И. Никишина, А.К. Тарханов; Воронежский ГАСУ. - Воронеж, 2012. – 53 с.

Содержит шесть лабораторных работ по курсу «Физика – электричество и магнетизм». Каждая работа сопровождается краткими теоретическими сведениями, контрольными вопросами, примерами контрольных задач и необходимым справочным материалом для выполнения.

Предназначен для студентов всех специальностей дневной формы обучения.

Ил. 33. Табл. 12. Библиогр.: 5 назв.

УДК 53.07 ББК 22.2:22. я7

ISBN 978-5-89040-407-7

© Белко В.Н., Никишина А.И., Тарханов А.К., 2012

© Воронежский ГАСУ, 2012

2

ВВЕДЕНИЕ

Основой физики как науки является эксперимент и его интерпретация. Методика проведения эксперимента и расчета, грамотное представление полученных результатов – важные составляющие этой дисциплины. Именно поэтому одной из форм фундаментальной подготовки студентов технических вузов является лабораторный практикум по физике. Его цель — закрепить знания студентов по курсу физики, познакомить их с основными методиками научно-технического эксперимента, развить навыки практического применения изучаемых физических явлений и законов, а также обучить работе с простейшими и наиболее распространенными измерительными приборами.

При подготовке к выполнению лабораторной работы студенту необходимо выполнить следующие требования:

1.Записать в специальной лабораторной тетради номер, название и цель данной лабораторной работы.

2.Выполнить схему и/или чертеж лабораторной установки.

3.Выписать необходимые для расчетов формулы с расшифровкой обозначений.

4.Карандашом начертить таблицы для записи величин, которые необходимо измерить или рассчитать в процессе выполнения данной лабораторной работы.

Для предоставления преподавателю отчета о проделанной работе

студент обязан:

1.Выполнить в тетради все расчеты в системе СИ.

2.Заполнить таблицы. Для всех величин в таблице должна быть записана соответствующая единица измерения.

3.Построить необходимые графики, соблюдая следующие правила:

-размер графика не менее половины страницы тетрадного листа.

-указать оси декартовой системы, на концах осей – стрелки, индексы величин, единицы измерений.

-на каждой оси указать масштаб (риски через равные промежутки, числа через равное количество рисок).

-на графике точки отмечать четко.

4.Сделать письменные выводы.

3

Правила техники безопасности

При выполнении лабораторных работ необходимо соблюдать следующие правила техники безопасности:

•входить в лаборатории и выполнять лабораторные работы только в присутствии и по разрешению преподавателя;

•не включать оборудование до тех пор, пока не поняты смысл и последовательность выполнения лабораторной работы;

•выполнять лабораторные работы следует строго в соответствии с рабочим заданием. Отклонения от рабочего задания без разрешения преподавателя не допускаются;

•электропитание установки включать только с разрешения преподавателя (или лаборанта) после ознакомления с описанием данной лабораторной работы и окончания сборки установки!

•во время выполнения лабораторной работы все изменения в электрической схеме установки производить только при отключенном питании;

•при обнаружении нарушений в электрической цепи лабораторной установки немедленно обесточить прибор и позвать лаборанта или преподавателя. Не пытаться устранить неполадки самостоятельно.

4

ЛАБОРАТОРНАЯ РАБОТА №1

ИЗМЕРИТЕЛЬНЫЙ МОСТ УИТСТОНА

1.1. Цель работы

Усвоение понятий силы и плотности электрического тока, электрического сопротивления и удельного сопротивления проводника, подвижности свободных носителей электрического заряда.

Знакомство со схемой измерительного моста Уитстона и условием его баланса.

Определение сопротивлений резисторов и проволочных металлических проводников, удельного сопротивления металла и подвижности свободных электронов.

1.2. Теоретические сведения

Электрический ток. Сопротивление проводников

Электрическим током называется упорядоченное движение свободных носителей электрического заряда. Вещества, в которых возможно такое движение, являются проводниками электричества, а электрический ток, возникающий в проводниках, представляет собой ток проводимости.

Для существования электрического тока в проводнике необходимо, во-первых, наличие свободных носителей электрического заряда, и, вовторых, наличие электрического поля, энергия которого затрачивалась бы на перемещение этих носителей заряда.

Специально поставленные опыты показали, что в металлах носителями электричества являются свободные электроны.

В отличие от металлов электрический ток в электролитах и газах (проводники II рода) обусловлен направленным движением как отрицательных, так и положительных ионов.

Одной из характеристик электрического тока является величина заряда, переносимого через поперечное сечение проводника в единицу времени. Эта характеристика называется силой тока:

.

Если же величина заряда, переносимого через поперечное сечение проводника, не зависит от времени, ток называется постоянным (стационарным). Тогда сила тока

.

За единицу силы тока принимается 1 ампер (А). Определение 1 ампера связано с электромагнитными действиями тока. Но при силе постоянного

5

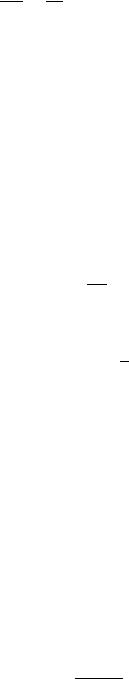
тока в 1 А через поперечное сечение проводника за время, равное 1 с, проходит заряд в 1 Кл.

За направление тока (по установившейся традиции) принимается направление движения носителей положительно заряда.

Электрический ток может быть распределен по сечению проводника неравномерно. Распределение тока по сечению характеризуется плотностью электрического тока:

.

Плотность тока – вектор, направленный вдоль тока и численно равный количеству электричества, протекающему за единицу времени через единичную площадку, ориентированную перпендикулярно току. Размер-

Зная вектор плотности тока в каждой точке проводника, можно найти силу тока через любую поверхность:

Физическая величина, численно равная полной работе, которая совершается кулоновскими и сторонними силами при перемещении вдоль участка цепи единичного положительного заряда называется напряжением (падением напряжения):

ε.

Здесь ε электродвижущая сила (ЭДС) – физическая величина, численно равная работе сторонних сил по перемещению заряда:

ст,

а разность потенциалов (φ1 – φ2) – физическая величина, численно равная работе кулоновских сил по перемещению заряда:

.

Когда на участке не действуют сторонние силы, напряжение равно разности потенциалов:

.

Единица измерения напряжения – [В]. Опыт показывает, что отношение разности потенциалов на концах проводника к силе тока в нем не зависит от режимов в цепи и при неизменной температуре остается для данного участка цепи постоянным. Для другого проводника, сделанного из другого материала и других размеров, это отношение будет иным, но оно также будет оставаться постоянным при неизменной температуре и любых изменениях разности потенциалов на его концах и силы тока в нем.

Этот факт приводит к заключению, что каждый проводник можно охарактеризовать отношением разности потенциалов на концах проводника к силе тока в нем:

– .

6

Величина R получила название электрического сопротивления проводника (в дальнейшем просто сопротивления). В СИ за единицу сопротивления принимается сопротивление такого участка, в котором при разности потенциалов на его концах в 1 В течет постоянный ток в 1 А. Эта единица сопротивления проводника получила название Ом.

Тогда из определения сопротивления проводника следует, что

Соотношение (1.1) получило название закона Ома для однородного (включающего только сопротивление R) участка цепи.

Электронная теория проводимости металлов дает закон Ома в дифференциальной форме, связывая плотность тока с напряженностью электри-

ческого поля , наложенного на проводник, т.е.

где σ – удельная электропроводность, а ρ – удельное электросопротивление металлического проводника.

Сопротивление однородного металлического цилиндрического проводника. Удельное сопротивление металла

Опыт показывает, что сопротивление металлического цилиндрического проводника прямо пропорционально его длине l, обратно пропорционально площади поперечного сечения проводника S и зависит от свойств металла, из которого изготовлен проводник. В качестве характеристик этих свойств выступает удельное электросопротивление металла ρ, которое зависит от температуры, давления, но не зависит от геометрических размеров проводника.

Связь между сопротивлением однородного цилиндрического проводника R, длиной проводника l, площадью поперечного сечения проводника S и его удельным сопротивлением определяется эмпирической формулой

Удельное электросопротивление проводника в СИ измеряется сопротивлением проводника длиной в 1 м и с площадью сечения в 1 м2. Следовательно, размерность удельного сопротивления в СИ

Тогда размерность удельного сопротивления

Ом·ммм ,

т.е. удельное сопротивление проводника численно равно сопротивлению проводника длиной в 1 м и с площадью сечения в 1 мм2.

7

Подвижность свободных электронов металлического проводника

Основной закон движения свободных носителей электрического заряда в проводнике, находящемся в электрическом поле, гласит: плотность электрического тока в проводнике пропорциональна заряду, концентрации

Принято упорядоченное движение свободных носителей заряда характеризовать их подвижностью. Подвижность носителей заряда есть средняя скорость их упорядоченного движения при напряженности электрического поля, равной единице напряженности. Если обозначить подвижность

Нетрудно связать подвижность свободных носителей заряда u0 с удельным электросопротивлением проводника ρ. Приравнивая правые части формул (1.2) и (1.4) и имея ввиду, что для металлического проводника q=e (заряд электрона), получим

.

Откуда

Для всех металлических проводников концентрация свободных электронов n≈1028 м-3.

Формула (1.6) используется для определения подвижности свободных электронов, если известно удельное электросопротивление металлического проводника.

Метод одинарного моста сопротивлений (мост Уитстона)

Д

Рис. 1.1

8

Наиболее простым методом определения электрического сопротивления проводников является метод одинарного моста, используемый в данной работе. Мост Уитстона состоит из известных сопротивлений R1, R2 и R и измеряемого сопротивления RX, соединенных по схеме, представленной на рис. 1.1.

В одну из диагоналей четырехугольника сопротивлений включается источник питания, в другую – чувствительный амперметр (нульгальванометр). При произвольном соотношении сопротивлений R1, R2 и R после включения источника питания через все элементы моста протекает электрический ток. Процесс измерения RX заключается в том, чтобы подбором сопротивлений R1, R2 и R добиться отсутствия тока в цепи амперметра.

Когда в цепи амперметра отсутствует ток, то для токов в остальных

Соотношение (1.11) известно как условие баланса моста.

1.3.Описание экспериментальной установки

εК

Рис. 1.2

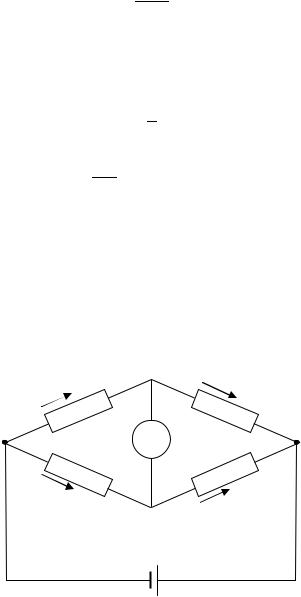
Схема экспериментальной установки приведена на рис. 1.2. От источника постоянного тока ε через ключ К идут провода к точкам А и В. Эти точки соединяются однородной тонкой проволокой, натянутой на линейку

9

с делениями (реохорд). Параллельно к реохорду к точкам А и В присоединяются неизвестное сопротивление RX (резистор) и магазин сопротивлений М с введенным в нем определенным сопротивлением R. От точки С идет проводник через гальванометр G к подвижному контакту D, который можно перемещать вдоль реохорда. Движок D делит тонкую проволоку на две части. Одна часть длиной l1 соответствует сопротивлению R1, другая длиной l2 соответствует сопротивлению R2 в схеме моста (рис. 1.1). Перемещая движок D по проволоке, т.е. меняя длины l1 и l2, можно изменять сопротивления R1 и R2.

ловия баланса моста Уитстона (1.11) величина неизвестного сопротивления определяется по формуле

Таким образом, для измерения RX необходимо подобрать такие значения R, l1 и l2, чтобы в цепи амперметра отсутствовал ток. В состав установки входят источник питания, мультиметр, набор резисторов различного сопротивления, часть из которых с закодированными значениями сопротивлений, а часть – с известными значениями сопротивлений; реохорд – доска с металлической нитью и измерительной линейкой; доска с укрепленными на ней металлическими проволочными резисторами, имеющими одинаковую длину, но различный диаметр; соединительные провода.

1.4. Порядок выполнения работы

Лабораторную работу необходимо выполнять, строго соблюдая правила техники безопасности, установленные в лаборатории электричества и магнетизма.

1.Собрать схему одинарного моста (рис. 1.2), не включая источник пи-

тания.

2.После проверки рабочей схемы преподавателем провести измере-

ние сопротивлений трех резисторов. При измерении RX1 установить в магазине М сопротивлений R=330 Ом; при измерении RX2 установить в магазине М сопротивлений R=150 Ом; при измерении RX3 установить R=680 Ом.

3.Включить источник питания в сеть.

4.Перемещая движок D по проволоке моста, добиться отсутствия

тока в цепи амперметра. Соответствующие значения длин l1 и l2 занести в табл. 1.1.

5.По формуле (1.12) рассчитать значения сопротивлений RX1, RX2, RX3.

10