Учебное пособие 1804

»[R,HOW]=simple(cos(x)+i*sin(x))

R = exp(i*x) HOW = convert(exp)

»[R,HOW]=simple(cos(3*acos(x)))

R = 4*x^3-3*x HOW = expand

Функция [N,D] = numden(A) преобразует каждый элемент массива А в рациональную форму в виде отношения двух неприводимых полиномов с целочисленными коэффициентами. При этом N и D - числители и знаменатели каждого преобразованного элемента массива. Пример:

» [n, d]=numden(x*y+y/x) n =

y*(x^2+1) d =

x

Одной из самых эффектных и часто используемых операций символьной математики является операция подстановки. Она реализуется функцией subs, имеющей ряд форм записи:

subs(S) заменяет в символьном выражении S все переменные их символьными значениями, которые берутся из вычисляемой функции или рабочей области системы MATLAB;

subs(S,NEW) - заменяет все свободные символьные переменные в S из списка NEW;

subs(S,OLD,NEW) - заменяет OLD на NEW в символьном выражении S. При одинаковых размерах массивов OLD и NEW замена идет поэлементно. Если S и OLD - скаляры, a NEW - числовой массив или массив ячеек, то скаляры расширяются до массива результатов;

если подстановка subs(S, OLD ,NEW) не меняет S, то выполняется подстановка subs(S, NEW, OLD);

subs(S, OLD, NEW, 0) - исключает попытку обратной подстановки. Примеры:

» subs(x-y,y,1) ans =

x-1

» subs(sin(x)+cos(x),[x,y],[a,b]) ans =

sin(a)+cos(a)

Для решения систем алгебраических уравнений и одиночных уравнений служит функция solve:

solve(expr1,expr2,...,exprN,var1,var2,...varN) - возвращает значения пере-

менных vari, при которых соблюдаются равенства, заданные выражениями expri. Если в выражениях не используются знаки равенства, то полагается expri = 0;

solve(expr1,expr2,...,exprN) - аналогична предшествующей функции, но переменные, по которым ищется решение, определяются функцией findsym.

При отсутствии аналитического решения и при числе неизвестных, равных числу уравнений, ищется только одно численное решение, а не все решения. Результат решения возможен в следующих формах:

для одного уравнения и одной переменной решение возвращается в виде одномерного или многомерного массива ячеек;

при одинаковом числе уравнений и переменных решение возвращается в упорядоченном по именам переменных виде;

для систем с одним выходным аргументом решение возвращается в виде массива записей.

Примеры:

»solve(x^3-1,x)

ans =

[ 1]

[ -1/2+1/2*i*3^(1/2)] [ -1/2-1/2*i*3^(1/2)]

» solve(x^2+5*x+6,x) ans =

[ -3] [ -2]

»syms a b c

»solve(a*x^2+b*x+c)

ans =

[ 1/2/a*(-b+(b^2-4*a*c)^(1/2))] [ 1/2/a*(-b-(b^2-4*a*c)^(1/2))]

»s=solve('x+y=3','x*y^2=4',x,y) s =

x:[3x1 sym]

y:[3x1 sym]

»s.x

ans = [ 4] [ 1] [ 1]

Обратите внимание на то, что для задания уравнений в явном виде используются строковые выражения, когда уравнения заключаются в апострофы. Рекомендуется использовать графики функций или графики левой и правой части уравнений для получения графической интерпретации решений. Это особенно полезно в том случае, если решение носит множественный характер, поскольку функция solve дает только одно решение.

Для решения дифференциальных уравнений в форме Коши MATLAB имеет следующую функцию dsolve.

dsolve('eqn1','eqn2', ...) возвращает аналитическое решение системы дифференциальных уравнений с начальными условиями. Они задаются равенствами eqni (вначале задаются уравнения, затем начальные условия).

По умолчанию независимой переменной считается переменная 't', обычно обозначающая время. Можно использовать и другую переменную, включив ее в конец списка параметров функции dsolve. Символ D обозначает производную

по независимой переменной, то есть ddt , при этом D2 означает d 2 dt 2 и так

далее. Имя независимой переменной не должно начинаться с буквы D. Начальные условия задаются в виде равенств 'у(а) = b' или 'Dy(a) = b', где

у независимая переменная, а и b константы. Если число начальных условий меньше, чем число дифференциальных уравнений, то в решении будут присутствовать произвольные постоянные Cl, C2 и так далее. Правила вывода подобны приведенным выше для функции solve.

Примеры применения функции dsolve:

» dsolve('D2x=-2*x')

ans = C1*sin(2^(1/2)*t)+C2*cos(2^(1/2)*t)

» dsolve('D2y=-2*x+y','y(0)=1','x')

ans = 2*x+C1*sinh(x)+cosh(x)

Часто возникает необходимость в задании функции, обратной по отношению к заданной функции f. Для этого в Symbolic имеется функция обращения finverse, которая задается в двух формах:

g = finverse(f) - возвращает функцию, обратную f Считается, что f - функция одной переменной, например 'х'. Тогда g(f(x)) = х;

g=finverse(f, v) - возвращает функцию, обратную f, относительно заданной переменной v, так что g(f(v)) = v. Эта форма используется, если f - функция ряда переменных.

Примеры:

» finverse(sinh(x))

ans = asinh(x)

» finverse(exp(x)) ans =

log(x)

К числу часто встречаемых в символьной математике манипуляций с функциями относится суперпозиция функций, реализуемая функциями compose:

compose(f,g) - возвращает f(g(y)), где f = f(x) и g = g(y). Независимые переменные х и у находятся с помощью функции findsym;

compose(f,g,z) - возвращает f(g(z)), где f = f(x), g = g(y);

compose(f,g,x,z) - возвращает f(g(z)) и при этом рассматривает х как независимую переменную х для функции f. Так, если f = cos(x/t), то compose(f,g,x,z) возвращает cos(g(z)/t), a compose(f,g,t,z) возвращает cos(x/g(z)); compose(f,g,x,y,z) - возвращает f(g(z)) и рассматривает х как независимую переменную для функции f и у - как независимую переменную для функции g.

Для f = cos(x/t) и g=sin(y/u) compose(f,g,x,y,z) возвращает cos(sin(z/u)/t), a compose(f,g,x,u,z) возвращает cos(sin(y/z)/t).

Примеры:

»f=1/(1+x^2); g=sin(y); h=x^t; p=exp(-y/u);

»compose(f,g)

ans = 1/(sin(y)^2+1)

» compose(f,g,t) ans = 1/(sin(t)^2+1)

» compose(h,g,x,z) ans =

sin(z)^t

» compose(h,g,t,z) ans =

x^sin(z)

» compose(h,p,t,u,z) ans =

x^exp(-y/z)

Чтобы избавить пользователя от возни с вполне возможным построением графиков функций с помощью стандартных средств (например, команды plot), в пакет Symbolic введены довольно удобные команды класса ezplot:

ezplot(f) - строит график символьно заданной функции f(x) независимой переменной 'х'. Она определена в интервале [-2*pi, 2*pi];

ezplot(f, xmin, xmax) или ezplot(f, [xmin, xmax]) - делает то же, но позволяет задать диапазон изменения независимой переменной х от xmin до хmах;

ezplot(f, [xmin xmax], fig) - обеспечивает спецификацию графика с помощью параметра fig.

Команды класса ezplot позволяют строить графики функций, имеющих особенности более наглядно, чем функция plot. Примером такого рода является построение графика функции tan(x), имеющего разрывы:

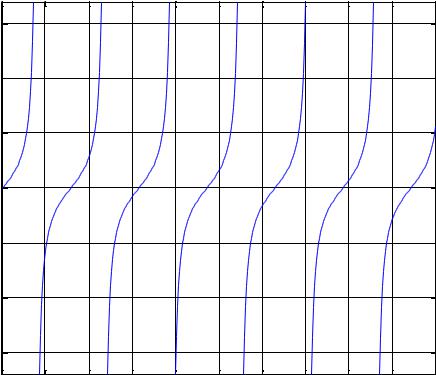
ezplot('tan(x)',0,20);grid on

В заключение приведем краткое описание еще нескольких функций работы с символьными переменными, доступными в системе MATLAB

2.1.Общая характеристика. Демонстрация возможностей ………….. 54

2.2.Библиотека модулей (блоков) …………………………………….. 59

2.2.1.Раздел Sources (Источники) ……………….……………….. 60

2.2.2.Раздел Sinks (Получатели) ………………………..………... 66

2.2.3.Раздел Discrete (Дискретные элементы) ………………….. 73

2.2.4.Раздел Linear (Линейные элементы) ………………………. 75

2.2.5. Раздел Nonlinear (Нелинейные элементы) ………………… 77

2.2.6.Раздел Connections (Соединительные узлы) ………………. 84

2.2.7.Дополнительные разделы библиотеки

(Blocksets & Toolboxes) …….…………..…………………... 87

2.3.Меню пользователя …………………………….…..………………. 88

2.3.1.Раздел File ………………………………..………………….. 88 2.3.2. Раздел меню пользователя Edit ……………………..……... 91

2.3.3.Раздел меню пользователя Simulation ……………………... 93

2.3.4.Раздел меню Format ……………………………..…………. 97

2.4.Использование подсистем ……………………….………………... 99

2.5.Маскирование подсистем ………………………….……………… 105

3.Работа с пакетом Сontrol system toolbox …………………………………. 114

3.1.Линейные стационарные объекты (lti-объекты) ……………..….. 114

3.2.Извлечение информации об lti-объектах ……………..…………... 115

3.3.Родовые свойства lti-объекта ……………..……………………….. 117

3.4.Чтение и установка значений ………………………………..……. 118

3.5.Функции создания и преобразования lti-моделей ……………...… 121

3.6.Преобразование lti-моделей ……………………………..………… 124

3.7.Переопределение базисных функций ………………………..…… 126

3.8.Соединение lti-моделей ……………………..……………………... 128

3.9.Получение lti-объекта из системы Simulink …………………..….. 133

3.10.Операторы и функции для анализа систем …………..…………. 134

3.11.Средства графического интерфейса пользователя для анализа

lti-систем …………………….………………………………….. 147

4.Выполнение символьных операций ………………..…………………….. 150

4.1.Возможности пакета Symbolic Math Toolbox …………………..… 150

4.2.Демонстрационные примеры работы с пакетом Symbolic …..….. 150

4.3.Задание символьных переменных с помощью апострофов ..…… 151

4.4.Базовые символьные функции …………………………………….. 152

Список литературы ………………..…………………………………………. 165