
Неопределенный и определенный интегралы. методические указания и контрольные задания к расчету № 3 по курсу математики. Муштенко В.С., Стенюхин Л.В
.pdf4.3. Объем тела вращения
Если криволинейная трапеция, имеющая основанием отрезок a ≤ x ≤ b , вращается вокруг оси OX , то объем полученного тела вращения вычисляется по формуле
b
V =π∫( f (x))2 dx ,
a
где y = f (x) - уравнение кривой, ограничивающей криволинейную трапецию сверху.
Если тело получено от вращения вокруг осиOX фигуры, ограниченной кривыми y = f1 (x) и y = f2 (x) ( f1 (x) ≤ f2 (x) ) и прямыми x = a и x = b , то объем тела вращения равен
V =πb∫[(f2 (x))2 −(f1 (x))2 ]dx .
a
Если криволинейная трапеция, имеющая основанием отрезок c ≤ y ≤ d , вращается вокруг оси OY , то объем такого тела вращения вычисляется по формуле
d
V =π ∫(ϕ( y))2 dy ,
c
где x =ϕ( y) - уравнение кривой, ограничивающей криволинейную трапецию справа.
Если тело получено от вращения вокруг оси OY фигуры, ограниченной кривыми x =ϕ1 ( y) и x =ϕ2 ( y) и прямыми y = c и y = d , то объем тела вращения равен
V =πd∫[(ϕ2 ( y))2 −(ϕ1 ( y))2 ]dy .
c
4.4. Некоторые физические задачи
4.4.1. Путь, пройденный телом
Если материальная точка движется по некоторой прямой со скоростью v = f (t) , то путь S , пройденный ею за промежуток времени α ≤ t ≤ β , вычисляется по формуле
β
S = ∫ f (t)dt .
α
21
4.4.2. Работа переменной силы
Пусть под действием силы F = f (x) материальная точка движется по прямой. Работа A этой силы на участке пути [a,b] определяется по формуле
b
A = ∫ f (x)dx .
a
4.4.2 Давление жидкости
Для вычисления силы давления жидкости используется закон Паскаля, согласно которому давление жидкости на площадку равно ее площади S , умноженной на глубину погружения h , на плотность ρ и ускорение силы
тяжести g , то есть
P = ρ g h S .
22
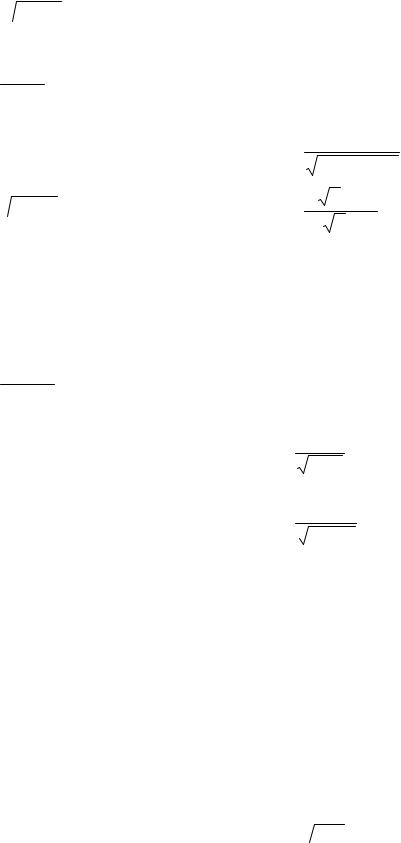
ВАРИАНТЫ КОНТРОЛЬНЫХ ЗАДАНИЙ
1.1) ∫ x x2 −5 dx ;
x2 −5 dx ;
2)∫1 −52x dx ;
3)∫sin(1 −3x) dx ;
4)∫ cos3 x sin x dx ;
cos3 x sin x dx ;
5)∫ x2ex dx ;
6)∫ln x dx ;
7)∫ x3 +1 x2 dx ;
2. 1) |
3 |
|
|
∫ y ln( y −1) dy ; |
|||
|
2 |
|
|
|
+∞ |
x |
|
3. 1) |
0∫ |
|
dx ; |
16x4 +1 |
|||
4.y = x2 , y = 3 −2x .
5.ρ = 3cosϕ , 0 ≤ϕ ≤ 2π .
6.y = 2x − x2 , y = x , (OX).
Вариант 1
8) ∫ |
|
|
x3 |
dx ; |
||||
x2 |
+ x +1 |
|||||||
|
|
|
|
|
||||
9) ∫ |
|
|
5x −1 |
|
|
|
dx ; |
|
3x |
2 −2x +1 |
|||||||
|
|
|||||||
|
|
|
1 |
|
|
|
|
|
10) |
∫ |
|
x2 −4x +5 dx ; |
|||||
11) |
∫ |
|
x −1 |
|
dx ; |
|||
|
|
x( x +1) |
|
|
|
|||
12) |
∫ |
|
dx |
|
; |
|
||
5 |
−3cos x |
|
||||||
|
|
|
|
|
||||
13) |
∫ |
cos3 x |
dx ; |
|||||
4 |
+sin x |
|||||||
|
|
|
|
|
|
|||
14) ∫sin 3x cos 2x dx .
2) |
8 |
|
x dx |
. |
∫ |
|
x +1 |
||
|
3 |
|
|
|
2) |
∫ |
|
dx . |
|
|
1 |
|
|
|
|
0 |
3 |
2 −4x |
|
7. |
3 |
от x = 0 до x = 5 . |
|
y = x |
2 |
||
8. |
x = 2 cos3 t , y = 2 sin3 t . |
||
9. Скорость тела задается формулой v =  1 +t м/с. Найти путь, пройденный телом за первые 10 с после начала движения.
1 +t м/с. Найти путь, пройденный телом за первые 10 с после начала движения.
23
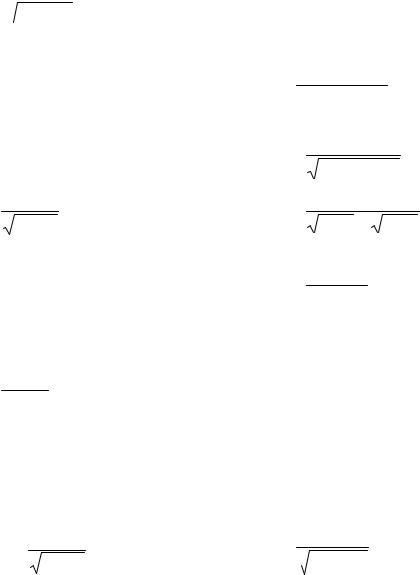
1. 1) ∫ x 2 −3x2 dx ;
2 −3x2 dx ;
2) |
∫ |
x2 |
dx ; |
||
x3 |
−2 |
||||
|
|
|
|||
3)∫cos (2 +6x) dx ;
4)∫ xx−2 +21 dx ;
5)∫ xe−x dx ;
6)∫( x +1) ln x dx ;
7)∫ xx2 −+1x dx ;
Вариант 2
8) ∫ |
|
x2 |
|
dx ; |
|
x2 |
+ x +1 |
||||
|
|
||||
1
9) ∫ 3x2 −2x +4 dx ;
10) |
∫ |
2x +1 |
dx ; |
|
|
5 −4x − x2 |
|
11) |
∫ |
x +1 |
x +1 dx ; |
x +1 −4 |
|||
12)∫ 2 +dxsin x ;
13)∫sin2 3x dx ;
14)∫sin 3x sin x dx .
π
2. |
|
π |
2 cos x dx ; |
|
||
1) |
∫ x |
|
||||
|
|
0 |
|
|
|
|
3. |
1) |
+∞ |
4x |
3 |
dx ; |
|
∫ |
|
|
||||
|
|
0 |
x4 +1 |
|
|
|
4. |
y = x2 , y = 4x −3. |
|
||||
5. |
ρ = 3(1 +cosϕ) , 0 ≤ϕ ≤ 2π . |
|
||||
6. |
y = 2x − x2 , y = 0 , (OX). |
|
||||
7. |
y = ln cos x от x = 0 до x = |
π . |
||||
|
|
|
|
|
|
6 |
2) |
∫3 tg2 x dx . |
|
||
|
π |
|
|
|
|
4 |
|
|
|
2) |
∫ |
|
dx |
. |
|
3 |
|
|
|
|
1 |
3 |
(3 − x)2 |
|
8.x = 2(cos t +t sin t) , y = 2(sin t −t cos t) , 0 ≤ t ≤π .
9.Вычислить работу, которую нужно затратить на сооружение конического кургана, радиус основания которого R = 2 м, а высота H = 3м, из одно-
родного строительного материала плотностью δ = 2,5т/ м3 .
24
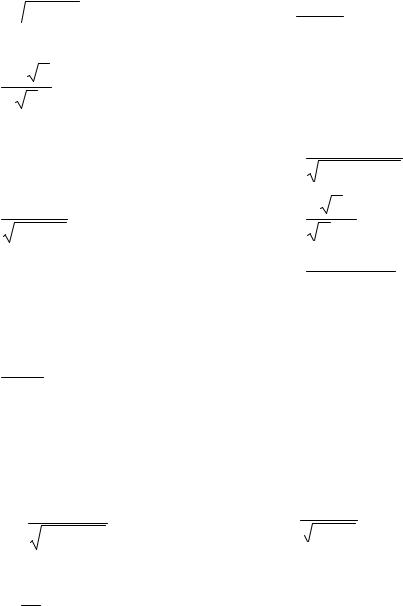
Вариант 3
1.1) ∫ x2  2 +5x3 dx ;
2 +5x3 dx ;
2)∫ sin x x dx ;
3)∫e2+7 x dx ;
4) ∫ |
|
x3 |
1 |
dx ; |
|
|
−2x4 |
5)∫ x2ex dx ;
6)∫ln(x +2) dx ;
7)∫1 −1x3 dx ;
8)∫ x2 +1 dx ;
x2 + x
9) ∫ |
|
2x +5 |
dx ; |
|
x2 |
−6x +10 |
|||
|
|
|||
|
|
1 |
|
|
10) ∫ |
2 −2x − x2 dx ; |
|||
11) ∫ 3 x x−5 dx ;
dx
12) ∫ cos x +sin x ;
13) ∫sin4 x dx ;
14) ∫sin 8x cos x dx .
π
2. 1) 2∫ x cos x dx ; |
ln 2 |
e |
x |
dx . |
||
2) ∫ |
|
|
||||
ex +3 |
||||||
0 |
0 |
|
||||
+∞ |
x |
2 |
|
0 |
|
dx |
. |
|
3. 1) ∫ |
( x3 +8)5 |
dx ; |
2) ∫ |
3 |
1 +3x |
|||
0 |
|
− |
1 |
|
|
|||
|
|
|
|
3 |
|
|
|
|
4.y = x2 , y = 5 x −2 . 2 2
5.ρ = 4 sin 2ϕ (четырехлепестковая роза).
6.y = 4x −2x2 , y = 0 , (OX).
7. |
y = ln sin x от x = π до x = |
2π |
. |
|
3 |
||||
|
3 |
|
||
8. |
x = 4 cos3 t , y = 4 sin3 t . |
|
|
|
9. |
Вычислить силу давления воды на прямоугольник, вертикально погру- |
|||
женный в воду, если известно, что его основание 8м, высота 12м, верхнее основание параллельно поверхности воды и находится на глубине 5м. Плот-
ность δ =1 кг/ м3 .
25
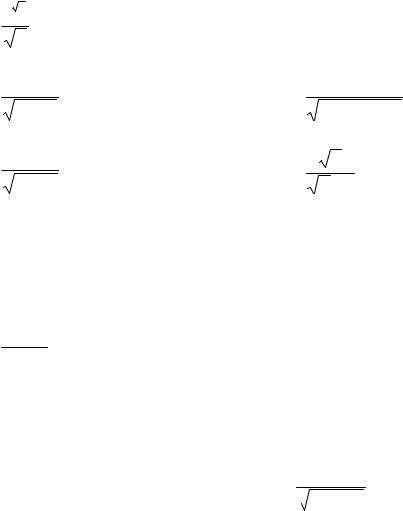
|
|
|
|
|
|
|
Вариант 4 |
|
|
|
|
|
|
|
||
1. 1) ∫ |
|
|
1 |
|
dx ; |
8) ∫ |
|
|
x3 |
|
dx ; |
|
|
|||
|
|
x ln x |
|
|
|
|
||||||||||
|
|
x |
2 −1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
2) ∫ |
e x |
dx ; |
|
9) ∫ |
|
|
6x +4 |
dx ; |
||||||||
|
x |
2 |
||||||||||||||
|
|
|
x |
|
|
|
|
−8x +4 |
|
|
||||||
3) |
∫ |
|
x |
|
dx ; |
10) |
∫ |
|
|
|
1 |
|
dx ; |
|||
|
|
|
1 − x4 |
|
|
|
|
x2 +4x +2 |
||||||||
4) |
∫ |
x +2 |
dx ; |
11) |
∫ |
|
x |
|
dx ; |
|
||||||
|
|
|
1 − x2 |
|
|
|
|
x −1 |
|
|
|
|||||
5) |
∫arctg x dx ; |
12) |
∫ |
|
|
|
dx |
|
; |
|||||||
cos x −sin x |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
6)∫cos(ln x) dx ;
7)∫ x +1x3 dx ;
2. 1) |
π |
sin x dx ; |
||
∫ x2 |
||||
|
0 |
|
|
|
3. 1) |
+∞ |
1 |
dx ; |
|
0∫ |
|
|||
π( x2 +4x +5) |
||||
4.y = x2 , y = 6 −5x .
5.ρ = 2(1 −cosϕ) , 0 ≤ϕ ≤ 2π .
6.y = 4x −2x2 , y = x , (OX).
13)∫sin2 x cos2 x dx ;
14)∫sin 2x cos 4x dx .
2ln 2 |
|
1 |
|
dx . |
|||
2) |
∫ |
|
|
||||
ex −1 |
|||||||
ln 2 |
|
||||||
2 |
|
x |
2 |
dx . |
|||
2) ∫ |
3 |
|
|||||
0 |
64 − x6 |
||||||
7. y = |
x2 |
от x = 0 до x = 2 . |
|
2 |
|||
|
|
8.x =5cos2 t , y =5sin2 t , 0 ≤ t ≤ π2 .
9.Скорость движения материальной точки v = 4te−t2 м/с. Какой путь пройдет точка от начала движения до полной остановки?
26
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 5 |
|
|
|
|
|
|
|
|
|
|
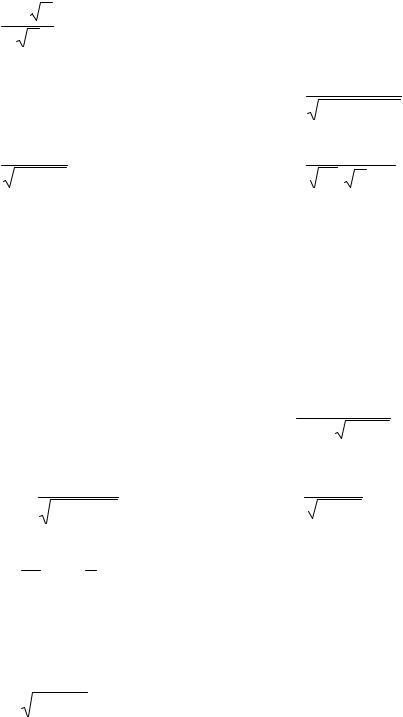
1. 1) ∫ |
|
2x +2 |
dx ; |
|
8) ∫ |
x3 +1 |
dx ; |
|
|
|
||||||||||||||
|
2 |
|
+2x |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
x |
|
|
|
|
|
x2 + x |
|
|
|
|
|
|
||||||||||
2) ∫ cos |
x |
dx ; |
|
9) ∫ |
|
|
1 |
|
|
|
|
dx ; |
||||||||||||
|
1 −3x − x |
2 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||||
3) ∫ |
|
|
|
|
x |
|
|
dx ; |
|
10) |
∫ |
|
5x −1 |
|
|
dx ; |
||||||||
1 |
+ x4 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
6 +4x − x2 |
||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
4) ∫ |
|
|
1 −2x2 dx ; |
|
11) |
∫ |
4 |
x3 ( |
x −1)dx ; |
|||||||||||||||
5) ∫ x arctg x dx ; |
|
12) |
∫ |
|
dx |
|
|
|
; |
|
||||||||||||||
|
3 |
+2 cos x |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
6) ∫ x 2x dx ; |
|
13) |
∫cos5 x dx ; |
|
|
|
||||||||||||||||||
7) ∫ |
|
x2 +1 |
dx ; |
|
14) |
∫cos3x cos5x dx . |
||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
x − x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
5 |
|
|
1 |
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
dx . |
|||||||
2. 1) |
|
∫arccos 2x dx ; |
|
|
|
|
|
|
|
|
||||||||||||||
|
2) ∫ |
2x + |
3x + |
|
||||||||||||||||||||
|
|
|
|
− |
1 |
|
|
|
|
|
|
0 |
|
1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
dx . |
|
|
|
|||||||
3. 1) |
|
∫ |
|
|
|
x |
dx ; |
2) ∫ |
|
|
|
|
||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
−∞ |
|
|
|
( x2 +4)3 |
|
0,5 9 1 −2x |
|
|
|
|
|
|||||||||
x2 x
4.y = 2 , y = 2 +3.
5.ρ = 4 cos 3ϕ .
6.y = 3x − x2 , y = 0 , (OX).
7.y = ( x −1)3 от x =1 до x = 6 .
8.x = 9(t −sin t) , y = 9(1 −cos t) , 0 ≤ t ≤ 2π .
9.Вычислить силу давления воды на прямоугольник, вертикально погруженный в воду, если известно, что его основание 2м, высота 3м, верхнее основание параллельно поверхности воды и находится на глубине 4м. Плот-
ность δ =1 кг/ м3 .
27
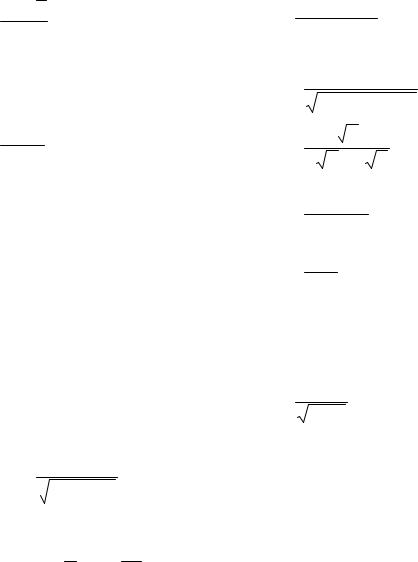
1.1) ∫ sin(lnx x) dx ;
x2 + 1
2)∫ x3 + 3x dx ;
3)∫tg x dx ;
4)∫ x4 x−3 dx ;
5)∫ x2 arctg x dx ;
6)∫ x e3xdx ;
7) ∫ |
|
x3 |
−1 |
|
dx ; |
|
||
x2 + x −2 |
|
|||||||
|
|
|
|
|||||
2. 1) |
π |
sin 2x dx ; |
|
|||||
∫ x |
|
|||||||
|
|
−π |
|
|
|
|
|
|
3. 1) |
+∞ |
|
x |
2 |
dx ; |
|||
∫ |
|
|
||||||
3 ( x3 +4)4 |
||||||||
|
|
0 |
|
|||||
4. y = 2x2 + 2x , y = 52x .
Вариант 6
8) |
∫ |
x |
3 +1 |
dx ; |
|
x3 |
− x2 |
||||
|
|
|
1
9) ∫ x2 +2x +2 dx ;
|
|
2x −1 |
|
10) |
∫ |
x2 +16x +60 dx ; |
|
11) |
|
3 x |
dx ; |
∫ 23 x +3 x |
|||
12)∫ sin x dx ; 3 +cos x
13)∫ tg13 x dx ;
14)∫sin 3x cos5x dx .
5 |
x |
dx . |
2) ∫ |
||
0 |
x +4 |
|
|
1 ln(3x −1) dx |
. |
||
2) ∫ |
3x −1 |
|||
|
1 |
|
|
|
3 |
|
|
||
5.ρ = 2ϕ , один виток спирали Архимеда и полярная ось.
6.xy = 4 , 2x + y −6 = 0 , (OX).
7.y =1 −ln cos x от x = 0 до x = π6 .
8.x = 7(t −sin t) , y = 7(1 −cos t) , 0 ≤ t ≤ 2π .
9.Скорость тела задается формулой v = 3t2 +2t +1 м/с. Найти путь, пройденный телом за первые 3 с после начала движения.
28

1. 1) ∫ |
cos(ln x) dx |
; |
|||
|
|
x |
|
|
|
2) |
∫ |
x5 |
|
dx ; |
|
x6 +10 |
|
||||
|
|
|
|
||
3) |
∫ctg x dx ; |
|
|||
4) |
∫ |
x +5 |
dx ; |
||
|
|
6 − x2 |
|
|
|
5)∫ x2 sin x dx ;
6)∫(x2 +9) ln x dx ;
x
7) ∫ ( x2 +3)( x −1) dx ;
2. 1) |
0 |
|
|
|
|
∫ x e−2 x dx ; |
|||||
|
− |
1 |
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
3. 1) |
+∞ |
4 |
dx ; |
||
1∫ |
|
||||
x(1 +ln2 x) |
|||||
Вариант 7
8) ∫ |
|
x3 +1 |
dx ; |
|
x2 |
−5x +6 |
|||
|
|
|
|
|
|
x |
|
|
|
9) ∫ |
|
x2 −4x +10 dx ; |
|||||
10) |
∫ |
|
|
|
8 |
dx ; |
|
4x2 +16x −20 |
|||||||
11) |
∫ |
6 |
x |
|
dx ; |
||
2 − |
3 |
x |
|||||
|
|
|
|
||||
12)∫sin3 2x dx ;
13)∫tg4 x dx ;
14)∫sin 3x sin 5x dx .
|
π |
1 |
|
|||
2) |
|
6∫ |
|
dx . |
||
|
|
|||||
|
|
0 cos x |
|
|||
2) |
|
∫ |
dx . |
|||
|
1 |
|
|
|
|
|
|
|
3 5 |
3 −4x |
|||
|
|
4 |
|
|
|
|
4.y = 3x2 + x , y = 4x .
5.ρ = 4sin2 ϕ .
6.y =  x , y = x3 , (OX).
x , y = x3 , (OX).
7.y = ( x +1)3 от x = −1 до x = 4 .
8.x =  3t2 , y = t −t3 .
3t2 , y = t −t3 .
9.Определить работу A , которую необходимо затратить, чтобы выкачать
воду из прямого кругового цилиндра. Радиус основания цилиндра R = 2м, высота h = 4м.
29

1. 1) ∫esin x cos x dx ;
2) ∫ |
2x −5 |
dx ; |
|
3 − x2 |
|
3)∫ arcctg2 x dx ;
x2 +1
4)∫sin(2x −7) dx ;
5)∫ x2 arcsin x dx ;
6)∫(x +2) cos 4x dx ;
x−2
7)∫ x3 + x2 + x −3 dx ;
|
π |
|
|
|
|
|
2. 1) |
∫3 tg2 x dx ; |
|
||||
|
0 |
|
|
|
|
|
3. 1) |
+∞ |
|
1 |
|
dx ; |
|
∫ |
|
|
|
|||
4x2 |
+4x +5 |
|||||
|
−1 |
|
||||
Вариант 8
8) ∫ |
2x5 −2x3 + x2 |
dx ; |
||||||
|
|
1 − x4 |
||||||
|
|
|
|
|
||||
9) ∫ |
|
|
3x +5 |
dx ; |
||||
|
|
|
x2 −4x +5 |
|
|
|||
10) |
∫ |
8 |
|
|
dx ; |
|||
x2 −6x +25 |
||||||||
11) |
∫ |
x |
dx ; |
|
|
|||
|
|
|
3 2x +3 |
|
|
|
|
|
12) |
∫ |
1 |
|
|
dx ; |
|||
2 −3cos x +sin x |
||||||||
13) |
∫cos2 3x sin 3x dx ; |
|||||||
14) |
∫cos 4x cos5x dx . |
|||||||
ln 3 |
1 |
|
dx . |
|
|
|||
2) ∫ |
|
|
|
|
||||
|
ex −e−x |
|
|
|||||
ln 2 |
|
|
|
|
||||
1 x dx
2)∫0 1 − x4 .
4.y = x2 , y = 2 − x2 .
5.ρ = cos 2ϕ .
6.y = ex , y = 0, x = 0 , x =1, (OX).
7.y =  x3 от x = 0 до x = 4 .
x3 от x = 0 до x = 4 .
8.x = 7(t −sin t) , y = 7(1 −cos t) , 0 ≤ t ≤ 2π .
9.Определить работу A , которую необходимо затратить, чтобы выкачать воду из полусферического сосуда, диаметр которого равен 20м, если плот-
ность воды δ =1 кг/ м3 .
30
