Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 1561

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

1.38 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 109 10 > Следующая >>>

x1(t) c1x11(t) x2 (t) c1x21(t)

c2 x12 (t) ...	cn x1n (t),
c2 x22 (t) ...	cn x2n (t),

xn (t) c1xn1 (t) c2 xn2 (t) ... cn xnn (t),

где c1, c2 ,..., cn — произвольные постоянные.

Случай, когда характеристическое уравнение имеет кратные корни, мы рассматривать не будем.

Пример 1. Решить систему

			dx1		x1	2x2 ,				dx2		2x1		x2
			dt		x1	2x2 ,				dt		2x1		x2
Ищем решение в виде						x				e t	, x		2	e t .
						1			1			2	2
Характеристическое уравнение
				2		0	или					2	2	3	0
	1			2

	2			1
	2			1
имеет корни			1	1,	2	3.
Система (3.3) для определения														1, 2	выглядит так:
(		1	)	1	2	2	0,								(*)
2			( 1		)		0.								(*)
2		1	( 1		)	2	0.
Подставляя в (*)						1, получаем
	x (t)		c	et		c	12	e 3t ,
1			1	11		2	12
	x (t)		c	et		c	12		e 3t ,
2			1	11		2	12
откуда 21			11 .
Следовательно, x						et , x		21				et	,
				11		11		21				11

Полагая в (*)				3, находим 22						12 , поэтому
	x	12	e 3t , x		22			12	e 3t .
	12	12			22			12
Общее решение данной системы:
x (t)	c	et	c	12		e 3t ,				x (t)	C et	C e 3t ,
1	1	11	2	12					или	1	1	2
x (t)	c	et	c				e 3t ,		или		C et	C e 3t .
x (t)	c	et	c	12			e 3t ,			x (t)	C et	C e 3t .
2	1	11	2	12						2	1	2

3.5. Решение систем дифференциальных уравнений методом интегрируемых комбинаций.

Этот метод интегрирования систем дифференциальных уравнений (не обязательно линейных) состоит в следующем: посредствам подходящих арифметических операций (например, сложение, вычитание др.) из уравнений заданной системы образуют так называемые интегрируемые комбинации, то есть достаточно просто интегрируемые уравнения вида

F t,u	du	0 ,
	dt

где u – некоторая функция		от искомых функций x1(t),
x2(t),…,xn(t).
Пример 1. Решить систему

y 2

x 2 .

Р е ш е н и е. Перепишем систему (2) в виде

xdx

y 2 dt

(3)

ydy

x 2 dt

Сложив почленно, получим

xdx

ydy

(x 2

y 2 )dt

или

d (x2

y 2 )

2dt,

y 2

Откуда

ln(x 2 y 2 )

2t ln C .

Потенцируя, будем иметь

x 2

y 2

C e2t .

(4)

Вычитая почленно из первого уравнения (3) второе, получим

xdx ydy ( y 2 x 2 )dt

или

	d (x2	y	2 )	2dt,
	x2	y 2		2dt,
	x2	y 2
отсюда
	x 2	y 2		C2 e 2t .	(5)

Разрешая (4) и (5) относительно x и y найдѐм общее решение системы (2):


x	~	2t	~		e	2t
x	C e		C		e
	1		2
y	~	2t	~		e	2t
y	C e		C	2	e
	1			2

где для упрощения записи положено

~ 1		~	1	C2 .
С1		С1 , C2
	2		2

Пример 2. Найти частное решение системы

dx	3x	5 y,

dt
dt		(6)
dy		(6)
dy	2x	8 y,

dt
dt

удовлетворяющее начальным условиям

x |t 0 2,

y |t 0 5.

(7)

Р е ш е н и е. Умножив первое уравнение на 2 и сложив

со вторым, получим

	d (2x y)	2(2x y),

	dt
	dt
отсюда

2x	y	C e2t ,
		1	(8)
	C e2t		(8)
y	C e2t	2x.
	1

Подставляя (8) в первое уравнение системы (6), получаем линейное уравнение для определения x:

					dx	7x	5C e2t .						(9)


					dt		1
					dt
x C		e 7t	5	C e2t .									(10)
x C	2	e 7t		C e2t .									(10)
	2		9		1
			9
Следовательно,
						y		1	C e2t	2C		e 7t .	(11)
						y			C e2t	2C	2	e 7t .	(11)
							9		1		2
							9

Выражение (10) и (11) представляют общее решение системы

(6).

Чтобы найти частное решение, удовлетворяющее условию (7), надо в (10) и (11) вместо t, x и y подставить соответственно числа 0, 2 и 5. Получим систему уравнений для определения C1 и C2:

2	C			5	C ,
2	C	2			C ,
		2		9	1
				9		(12)
		1				(12)
5		1	C		2C	,
5			C		2C	,
		9	1		2
		9

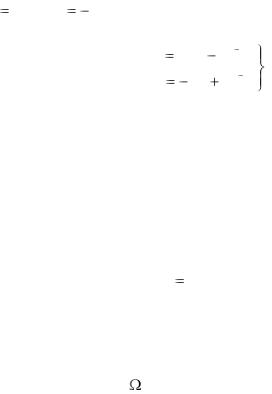
откуда
C1 9, C2	3.
Ответ:	x	5e2t	3e 7t ,
Ответ:	y	e2t	6e 7t . .

4.Элементы теории устойчивости

4.1. Зависимость решения от начальных данных

Рассмотрим вопрос о зависимости решения задачи Коши от начальных данных.

dx	f(t,x),	(1.1)

dt
dt

x(t0)=x0

Если функция f(t,x) непрерывна по совокупности аргументов и имеет ограниченную производную дf/дх в некоторой области изменения t, x, содержащей точку (tо, xo), то решение задачи Коши существует и единственно. Если изменять значения t0 и x0, то будет меняться и решение. Возникает важный в приложениях вопрос: как оно будет при этом меняться? Вопрос этот имеет и большое принципиальное значение. Действительно, если какая-либо физическая задача приводит к задаче Коши, то начальные значения находятся из опыта и за абсолютную точность измерения ручаться нельзя. И если сколь угодно малые изменения начальных данных способны сильно изменять решение, то математическая модель окажется мало пригодной для описания реального процесса.

Справедлива следующая теорема о непрерывной

зависимости решения от начальных условий

Теорема 1. Если правая часть f(t,x) дифференциального уравнения

dx/d t= f(t, x)

(1.1)

непрерывна по совокупности переменных и имеет ограниченную частную производную дf/дх в некоторой области G изменения t, x, то решение x(t)==x(t,to,хo),

удовлетворяющее начальному

условию

x(t0)=x0, где

(t0,x0)

G, непрерывно зависит от начальных данных.

Иными словами, пусть через точку (t0,x0) проходит

решение

x(t)

уравнения

(1.1),

определенное на

отрезке

, t0 ( ,

) . Тогда для любого >0 найдется

такое

>0, что при

< ,

решение

уравнения

(1.1),

проходящее

через

точку

x(t)

~ ~

] и отличается там от x(t)

(t0 , x0 ), существует на отрезке [

меньше чем на

x(t)

α, β

x(t)

Аналогичная теорема справедлива и для системы дифференциальных уравнений

dx i	fi	(t, x1 , x 2 ,..., x n ), i 1,2,..., n.
dt

При выполнении условий теоремы 1 решение задачи Коши существует, единственно и непрерывно зависит от начальных данных. В этом случае говорят, что задача Коши поставлена корректно. Существенным является то

обстоятельство, что отрезок [ , ] изменения t конечен.

Однако	во	многих задачах нас интересует зависимость
решения от начальных			данных в бесконечном промежутке
t0 t	.	Переход от	конечного промежутка, в котором

рассматривается непрерывная зависимость решения от начальных значений к бесконечному существенно меняет характер задачи и методы исследования. Эта проблема относится к теории устойчивости, созданной А. М. Ляпуновым (см. работу «Oбщая задача об устойчивости движения» (Гостехиздат, 1980)).

Для линейных систем

	dxi	n

		aij (t)xi	fi (t),	i	1,2,.., n,
	dt
		i 1
решение xi (t),i		1,2,..., n	существует			для t0 t
(глобальная теорема существования)					при условии, что
функции aij(t) и fi(t) — непрерывны на				t0 ,		, неограниченно

продолжаемо вправо и единственно. Не все системы обладают таким свойством.

Например, для скалярного уравнения

		dx / dt	x2			(1.2)
функция f(t,х)		х2 непрерывна и имеет производные всех
порядков по х. Нетрудно проверить, что функция					х=	/(1 -	t)
является решением задачи
		dx/dt=x2, x(0)= ,		>0.
Однако,	это решение		существует	только в	интервале
(- , 1/	),	зависящем от начального			условия,		и
непродолжаемо на полуинтервал (-				, 1/ ].
Уравнение (1.2) есть уравнение сверхбыстрого
размножения,		когда	прирост	пропорционален		числу

всевозможных пар. Его решение показывает, что при таком законе прироста населения количество населения становится бесконечным за конечное время (в то время как обычный закон прироста — экспоненциальный).

4.2. Устойчивость по Ляпунову. Основные понятия,

определения.
Рассмотрим дифференциальное	уравнение первого
порядка
dx/dt=f(t,x);	(2.1)

модель. Пусть шарик лежит на дне полусферической лунки (находится в положении равновесия). Если малым возмущением вывести шарик из этого положения, то он будет колебаться около него. При отсутствии трения, положение равновесия будет устойчивым, при наличии трения колебания шарика будут уменьшаться с возрастанием времени, т. е. положение равновесия будет асимптотически устойчивым.

Пример.1. Исследовать на устойчивость тривиальное решение х 0 уравнения.

						dx/df=0.
Решение	х		0,		очевидно,		удовлетворяет	начальному
условию					0 . Любое другое решение, удовлетворяющее
условию	х	t	t	0	0 . Любое другое решение, удовлетворяющее

начальному условию х						t t	x0 , имеет вид х х0.	Поэтому
							0
(рис. 6),

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 109 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20221.37 Mб6Учебное пособие 1557.pdf
#
30.04.20221.37 Mб151Учебное пособие 1558.pdf
#
30.04.20221.38 Mб3Учебное пособие 1559.pdf
#
30.04.2022306.09 Кб2Учебное пособие 156.pdf
#
30.04.20221.38 Mб2Учебное пособие 1560.pdf
#
30.04.20221.38 Mб3Учебное пособие 1561.pdf
#
30.04.20221.39 Mб10Учебное пособие 1562.pdf
#
30.04.20221.39 Mб3Учебное пособие 1563.pdf
#
30.04.20221.39 Mб3Учебное пособие 1564.pdf
#
30.04.20221.4 Mб3Учебное пособие 1565.pdf
#
30.04.20221.4 Mб2Учебное пособие 1566.pdf