
Учебное пособие 1561
.pdf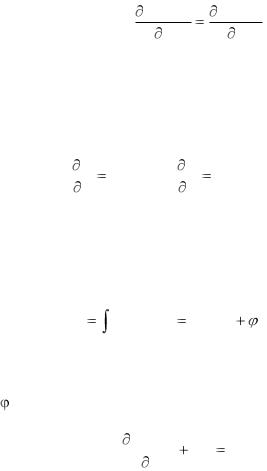
Для того, чтобы уравнение (6.1) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы
M(x, y) |
N(x, y) |
x y
Если U(x,y) известна, то все решения уравнения (6.1) удовлетворяют условию U(x,y) = С. где С - произвольная постоянная. Чтобы, найти функцию U(x,у) воспользуемся равенствами
U |
M(x, y), |
U |
N(x, y). |
|
|
|
|||
x |
x |
|||
|
|
(6.2)
Интегрируя первое из них по х, определим функцию U(x,y) с точностью до произвольной дифференцируемой функции:
U(x, y) |
M(x, y)dx ф(x, y) |
(y). |
(6.3) |
Дифференцируя (6.3) по у с учетом второго из равенств (6.2), получаем уравнение для определения функции
(у):
Ф(x, y) |
|
dφ |
N(x, y). |
|
|
|
|
y |
|
dy |
|
|
|
Пример 1. Решить дифференциальное уравнение
(sin xy + xy cos xy)dx + x2 cos xy dy = 0.

Р е ш е н и е. Проверим, что данное уравнение является уравнением в полных дифференциалах. Имеем
|
M |
|
|
(sin xy |
xy cos xy) |
x cos xy |
x cos xy |
|
x2 y sin xy |
|||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||||||
|
y |
y |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
= 2x cos xy x 2 y sin xy, |
|
|
||||||
|
|
|
|
|
|
N |
|
(x2 cos xy) |
2x cos xy |
x2 y sin xy, |
||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
x |
x |
|
|
|
|
|
|
|
|
|
||
т. е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
M |
|
N |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
y |
|
x |
|
|
|
|
|
Условие (2) выполнено. |
|
|
|
|
|
|
|
|
||||||||||
Далее, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
x |
|
|
|
|
y |
|
|
|
|
|
|
|
u(x, y) |
(sin xy |
xy cos xy)dx |
x 2 |
cos x |
0 |
ydy |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
x0 |
|
|
|
|
y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x sin xy |
x0 sin x0 y0 ; |
|
|
|
||||
так что |
|
|
x sin xy |
C |
x0 sin x0 y0 или |
x sin xy C1. |
||||||||||||
При интегрировании некоторых дифференциальных уравнений можно так сгруппировать члены, что получаются легко интегрируемые комбинации.
Пример 2. Решить дифференциальное уравнение
(x3 xy2 )dx (x 2 y y 3 )dy 0. (2 )
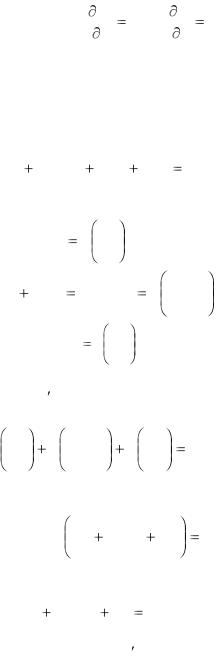
Р е ш е н и е. Здесь |
M |
2xy , |
N |
2xy , так что |
|
|
|
||||
y |
x |
||||
|
|
|
условие (2) выполнено и, следовательно, данное уравнение есть уравнение в полных дифференциалах. Но это уравнение легко привести к виду du=0 непосредственной группировкой его членов. С этой целью перепишем его так:
x3 dx xy( ydx xdy) y 3 dy 0. |
|
|
||||||||
Здесь |
|
|
|
|
|
|
|
|
|
|
x3 dx |
d |
|
x 4 |
|
, |
|
|
|
||
4 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||
xy( ydx xdy) |
xyd (xy) d |
(xy) |
2 |
, |
||||||
|
|
|||||||||
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
y 3 dy |
|
d |
y 4 |
. |
|
|
|
|||
|
|
|
|
|
||||||
|
|
|
|
|
4 |
|
|
|
|
|
Поэтому уравнение (2 ) можно записать в виде
|
x4 |
|
(xy)2 |
|
|
|
y 4 |
||||||
d |
|
|
d |
|
|
|
|
d |
|
|
0 |
||
4 |
|
2 |
4 |
||||||||||
|
|
|
|
|
|
|
|
||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 |
|
(xy)2 |
|
y 4 |
||||
|
|
|
d |
|
|
|
|
|
|
|
|
0, |
|
|
|
|
4 |
|
2 |
|
4 |
||||||
|
|
|
|
|
|
|
|||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2(xy)2 |
|
y 4 |
C |
|||||||
есть общий интеграл уравнения (2 ).
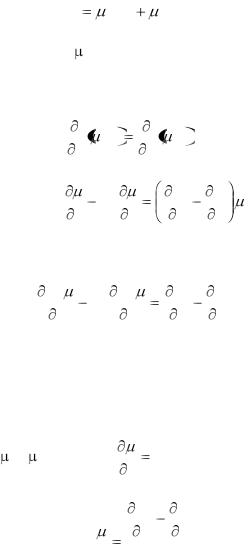
Внекоторых случаях, когда левая часть уравнения
(1)не является полным дифференциалом, удаѐтся
подобрать функцию 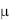 (x, y), после умножения, на которую левая часть (1) превращается в полный дифференциал
(x, y), после умножения, на которую левая часть (1) превращается в полный дифференциал
du Mdx Ndy. |
(4) |
Такая функция (x, y) называется интегрирующим множителем. Из определения интегрирующего множителя имеем
|
|
|
|
|
|
M |
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
y |
|
|
|
|
|
x |
|
|
|
|
|
||
или |
N |
|
|
|
|
M |
|
|
|
|
M |
|
|
N |
, |
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
y |
|
|
|
y |
|
|
x |
|||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
ln |
|
M |
|
ln |
|
|
|
M |
|
|
N |
. |
(5) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x |
|
|
|
y |
|
|
|
y |
|
|
x |
|
||||
Мы получили для нахождения интегрирующего множителя уравнения в частных производных.
Отметим некоторые частные случаи, когда удается сравнительно легко найти решение уравнения (5), т. е. найти интегрирующий множитель.
1. |
= (x). Тогда |
|
|
|
|
0 и уравнение (5) примет |
||||||
|
y |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
вид |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
M |
|
N |
|
|||
|
|
d ln |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
x |
. |
(6) |
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
dx |
|
|
|
|
N |
|
||||
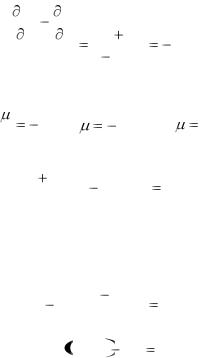
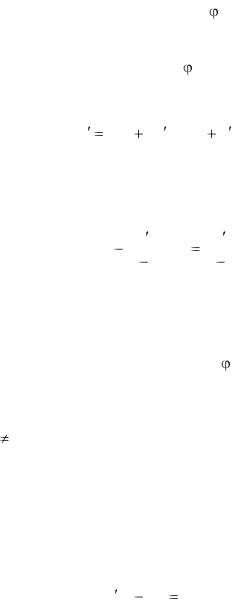
Для существования интегрирующего множителя, не зависящего от y, необходимо и достаточно, чтобы правая часть (6) была функцией только x. В таком случае ln 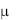 найдѐтся интегрированием по х.
найдѐтся интегрированием по х.
Пример 3. Рассмотрим уравнение
(x + y2) dx – 2xy dy = 0.
Р е ш е н и е. Здесь
M = x+y2, N = - 2xy.
Имеем
|
M |
N |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
y |
x 2 y 2 y |
|
2 |
. |
||||
|
|
|
|
|
|
|
|
||
|
|
N |
|
|
|
2xy |
|
x |
|
Следовательно,
d ln |
2 |
, |
ln |
2ln | x | , |
1 |
. |
|
|
|
|
|
||||
dx |
|
x |
|
|
|
x2 |
|
Уравнение
x y 2 |
dx 2 |
xy |
dy 0 |
|
x2 |
x2 |
|||
|
|
есть уравнение в полных дифференциалах. Его левую часть можно представить в виде
|
dx |
|
2xydy y 2 dx |
0 . |
|||
|
x |
|
x2 |
|
|
||
|
|
|
|
|
|||
Откуда |
d ln | x | |
x 2 |
|
0 |
|||
y |
|||||||
|
|
|
|
|
|||

и общий интеграл данного уравнения есть
|
|
|
|
y2 |
|
|
|
|
|
|
|
|
|
|
|
x |
C e x . |
|
|
|
|
|
|
|
|
||
2. |
Аналогично, |
если |
|
N |
M |
1 |
есть |
||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
x |
y |
M |
||||
|
функция, |
|
|
|
|
|
|
|
|
|
|
|
|
зависящая |
только |
от |
y, то |
уравнение |
(1) |
имеет |
|||||||
интегрирующий множитель |
= |
(y), |
зависящий |
||||||||||
только от y. |
|
|
|
|
|
|
|
|
|
|
|
|
|
1.7 Уравнения, неразрешенные относительно производной
Общего метода решения уравнений, неразрешимых относительно производной, нет. Если дифференциальное уравнение F(х,у,у ) = 0 разрешимо либо относительно искомой функции у = f(x.y'), либо относительно аргумента х = f(y,y ), то оно может быть проинтегрировано путем введения параметра р = у'. Исходное уравнение перейдет в алгебраическое, дифференцируя соответственно по х или по у, получим системы уравнений
y |
f(x, p), |
|
|
|
|
|
x |
f(y,p) |
|
|
|
|
|
|||||
p |
f |
|
|
f |
|
p |
, или |
|
1 |
|
f |
|
|
f |
|
p |
|
|
x |
p |
|
x |
|
p |
|
y |
p |
|
y |
|
|||||||
|
|
|
|
|
|
|
||||||||||||
решения |
|
которых |
находятся |
в |
|
|
явном |
иди |
||||||||||
параметрическом виде.
Рассмотрим, например, уравнение Лагранжа
у = xf(y')+ (y').
Введением параметра р=у' уравнение Лагранжа приводится к виду у = хf(р)+ (р). Дифференцируя по х, получим
y f(p) xf (p) |
dp |
φ (p) |
dp |
|
dx |
dx |
|||
|
|
или, после замены у' через р и алгебраических преобразований,
dx |
|
f (p) |
x |
φ (p) |
. |
|
|
|
|
||
dp |
|
p f(p) |
|
p f(p) |
|
Это линейное уравнение относительно х и производной
dx |
Его общий интеграл имеет вид Ф(х,р,С)=0. |
|
|
||
dp |
||
|
Совместно с уравнением
у = xf(y')+ (у)
он дает общий интеграл уравнения Лагранжа. Произведенное преобразование возможно лишь, если р- f(р) 0. Корни уравнения p-f(p)=0 дадут также решения уравнения Лагранжа, это особое решение, представляющее собой прямую линию. К уравнениям, не разрешенным относительно производной, приводят чаще всего различные геометрические задачи такие, как задачи об изогональных траекториях и др.
Пример 1. Найти общий интеграл уравнения:
( y )2 |
xy |
0 |
|
|
|||
a 2 |
|||
|
|
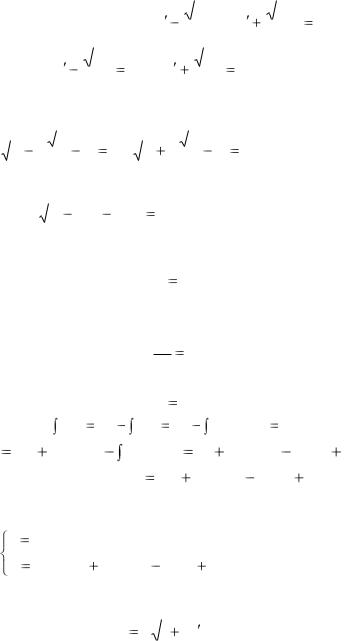
Р е ш е н и е: Разлагая левую часть уравнения на
множители получим: ( y |
|
|
xy |
|
) * ( y |
|
|
xy |
|
) 0 |
||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
a |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
откуда y |
|
xy |
|
0 |
и |
y |
|
|
xy |
|
0 |
. Оба эти уравнения |
||||||
|
|
|
|
|
|
|
|
|
||||||||||
a |
|
|
a |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
являются уравнениями с разделяющимися переменными. Их общие интегралы:
|
|
|
|
x |
|
x |
|
|
|
, |
|
|
x |
x |
|
C 0 . |
|
|
y |
|
|
C 0 |
y |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
3a |
|
|
3a |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Поэтому |
общий |
интеграл |
исходного уравнения имеет |
||||||||||||||
вид: ( |
|
|
|
|
|
C)2 |
|
x3 |
|
|
|
|
|
|
|||
|
y |
|
|
|
0 |
|
|
|
|
||||||||
|
|
9a2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 2: Найти общее решение уравнения
xy sin y
sin y
впараметрической форме.
Р е ш е н и е: Положим y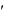
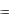 p ; тогда x
p ; тогда x 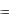 psin p .
psin p .
dy
Равенство p dx
перепишем в форме dy |
pdx, так как |
|
||||||
|
pdx |
px |
xdp |
px |
p sin pdp |
|
||
px |
p cos p |
cos pdp |
|
px p cos p |
sin p C. |
|||
то, следовательно, y |
px |
|
p cos p sin p |
C . Общее |
||||
решение запишется в следующем виде: |
|
|||||||
x |
p sin p, |
|
|
|
|
|
|
|
y |
p2 sin p |
p cos p |
sin p |
C. |
|
|||
|
Пример 3: Найти общее решение уравнения |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
y a |
1 |
( y )2 . |
|
||

Р е ш е н и е: |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Положим |
p |
y |
sht ; |
тогда |
y |
a 1 sh2t |
a * cht . Из |
||||
равенства |
dy |
|
p находим dx |
|
dy |
. Та как dy |
a * shtdt, |
||||
dx |
|
p |
|||||||||
|
|
|
|
|
|
|
|
|
|||
то dx adt и x |
at |
C . В параметрической форме общее |
|||||||||
решение запишется так: |
|
|
|
|
|
|
|
||||
|
|
|
x |
at |
C, |
|
|
|
|
|
|
|
|
|
y |
a * cht. |
|
|
|
|
|
|
|
Исключим параметр p. Для этого из первого уравнения
находим t |
и подставляем во второе. Имеем t |
x C |
и |
|||
a |
||||||
|
|
|
|
|
||
y a * ch |
x |
C |
. |
|
|
|
|
|
|
|
|||
|
|
a |
|
|
||
Пример 4: Найти общее решение уравнения:
y x( y )2 |
( y )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Р е ш е н и е: Положим, что y |
|
|
p . Тогда y |
xp2 |
p 2 , |
|||||||||
или y (x |
1) p 2 . Продифференцировав по x, имеем |
|||||||||||||
|
y |
p2 |
2(x |
1) p |
dp |
. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
После несложных преобразований получим |
|
|
|
|
||||||||||
|
1 |
p |
2(x |
|
1) |
dp |
|
, |
или |
|
|
|
|
|
|
|
dx |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
ln(x |
1) |
2ln(1 |
p) |
2lnC. |
|
|
|
|
|||||
|
|
|
|
|
находим: x 1 |
|
|
C 2 |
||||||
Произведя |
потенцирование, |
|
|
|
. |
|||||||||
(1 |
p)2 |
|||||||||||||
Следовательно, общее решение в параметрической форме примет вид:

x |
|
|
|
C 2 |
|
1, |
|
|
|
|
|||
(1 |
|
p)2 |
|
|
|
|
|||||||
|
|
|
. |
|
|
|
|
||||||
|
|
|
C 2 p 2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
y |
|
|
|
|
|
. |
|
|
|
|
|
|
|
(1 |
|
p)2 |
|
|
|
|
|
|
|||||
Исключим параметр p. Для этого найдем выражение |
|||||||||||||
ти подставим в уравнение |
y (x 1) p 2 . Таким образом, |
||||||||||||
общее решение y |
|
|
|
C)2 . |
|||||||||
( x 1 |
|||||||||||||
|
|
|
Пример 5:Найти общее решение уравнения |
||||||||||
y |
px |
|
1 |
, где |
p |
y . |
|
||||||
|
|
|
|||||||||||
|
|
|
|
|
p |
|
|
|
|
|
|
||
Решение: Общее решение получаем непосредственно из уравнения заменой p на C:
y Cx |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
C |
|
|
|
|
|
|
|
|
|
Для получения особого решения найдем ( p) |
1 |
. |
||||||||
|
||||||||||
|
|
|
|
|
|
|
|
|
p 2 |
|
Система уравнений |
|
|
|
|
|
|
|
|
||
|
|
|
x |
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p 2 , |
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
|
y |
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
p |
|
|
||
представляет |
собой |
|
|
|
|
особое решение в |
||||
параметрической |
форме. |
Исключим параметр |
p. Для |
|||||||
этого возведем обе части второго уравнения в квадрат и
разделим |
их на соответствующие части |
первого |
|||||
|
|
y 2 |
|
y |
2 |
4x . |
|
уравнения; |
получим |
|
4 , |
откуда |
|
||
|
|
||||||
|
|
x |
|
|
|
|
|
