
Учебное пособие 1561
.pdf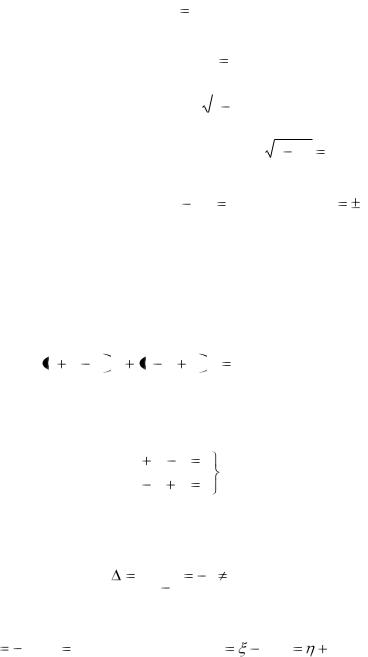
arcsin |
y |
|
ln Cx . |
|||
x |
||||||
|
|
|
|
|||
Отсюда ,общее решение будет: |
y xsinlnCx . |
|||||
При разделении переменных мы делили обе части |
||||||
|
|
|
|
|||
уравнения на произведение |
x 1 u 2 , поэтому могли |
|||||
потерять решения, которые обращают в нуль его
сомножители. Положим теперь |
|
x = 0 и |
1 u 2 |
0 . |
|
|
Но x = 0 не является решением уравнения, а из |
||||||
второго получаем, что 1 |
y 2 |
0 , |
откуда |
y |
x . |
|
x2 |
||||||
|
|
|
|
|
||
Непосредственной проверкой убеждаемся, что функции y = - x и y = x являются решениями уравнения.
Функции y = - x и y = x являются особыми решениями данного уравнения.
Пример 2. Решить уравнение
x y 2 dx x y 4 dy 0 . |
(1) |
Р е ш е н и е. Рассмотрим систему линейных алгебраических уравнений:
x y 2 0 . x y 4 0
Определитель этой систем:
|
|
|
1 |
1 |
2 |
0 . |
|
|
|
|
1 |
1 |
|
||
|
|
|
|
|
|
||
Следовательно, |
система |
имеет единственное |
решение |
||||
x0 |
1 , y0 3 . |
Делаем замену x |
1, y |
3 . |
|||
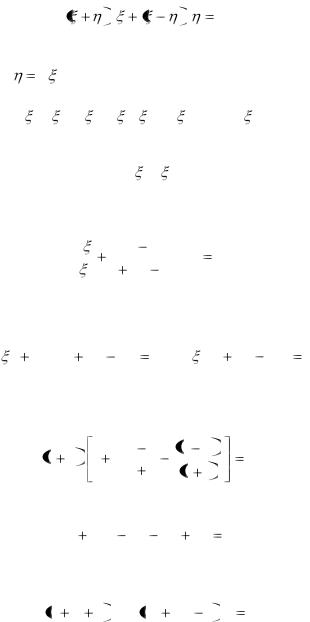
Тогда уравнение (1) примет вид |
|
|
|
d |
d |
0 |
(2) |
Уравнение (2) является однородным уравнением.
Полагая |
u |
, получим |
|
|
|
|
|
|||||
( |
+ |
u)d + ( |
- |
u )( |
du + u d ) = 0 |
|||||||
Откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1 + 2u – u2)d |
+ |
(1 - u)du = 0. |
||||||||
Разделяем переменные |
|
|
|
|
|
|||||||
|
|
|
|
d |
1 |
u |
|
du 0 . |
||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
2u |
u 2 |
|||||||
Интегрируя, найдѐм |
|
|
|
|
|
|||||||
ln | | |
1 |
ln | 1 2u u 2 |
| ln C ; |
2 (1 2u u 2 ) C . |
||||||||
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
Возвращаемся к переменным x, y:
x 1 |
2 |
1 2 |
y |
3 |
|
y |
3 2 |
|
C |
|
x |
1 |
|
x |
1 2 |
|
|||
|
|
|
|
|
|
||||
или |
|
|
|
|
|
|
|
|
|
x 2 |
|
2xy y 2 |
|
4x 8 y C . |
|
||||
Пример 3. Решить уравнение
x y 1 dx  2x 2 y 1 dy 0
2x 2 y 1 dy 0

Р е ш е н и е. Система линейных алгебраических уравнений
x y 1 0
2x 2 y 1 0
несовместна. Определитель системы
1 1
0
2 2
В этом случае метод, применѐнный в предыдущем примере, не подходит. Для интегрирования уравнения применяем подстановку
x + y = z, dy = dz – dx.
Уравнение примет вид
(2 – z)dx + (2z – 1)dz = 0.
Разделяя переменные, получим
dx |
2z |
1 |
dz |
0 . |
|
z |
2 |
||||
|
|
|
|||
Отсюда |
|
|
|
|
|
x 2z |
3ln | z |
2 | C . |
|||
Возвращаясь к переменным x, y получим общий интеграл данного уравнения
x 2y 3ln | x y 2 | C .
1.5. Линейные уравнения и уравнения, приводящиеся
к ним
Уравнения вида
y (х) + а(х)у(х) + b(х)=0 |
(5.1) |
называются линейными уравнениями первого порядка. При b(х)=0 уравнение (5.1) называется однородным уравнением. Существует несколько методов решения этого уравнения. Рассмотрим метод вариации произвольных постоянных, предложенный Ж.Л Лагранжем. Решение однородного уравнения представляется, очевидно, формулой
|
|
y0 (x) Ce |
a(x)dx . |
|||
Решение уравнения (5.1) находят в виде |
||||||
y(x) |
C(x)e |
a(x)dx . |
|
( |
||
5.2) |
|
|
|
|
|
|
Подставляя |
(5.2) |
в |
|
(5.1), получаем уравнение |
||
|
|
dC |
b(x)e |
a(x)dx |
. |
|
|
|
|
|
|
||
|
|
dx |
|
|
||
|
|
|
|
|
|
|
Откуда C(x) |
C |
b(x)e a(x)dx |
и, следовательно, общее |
|||
решение уравнения (5.1) имеет вид |
|
|||||
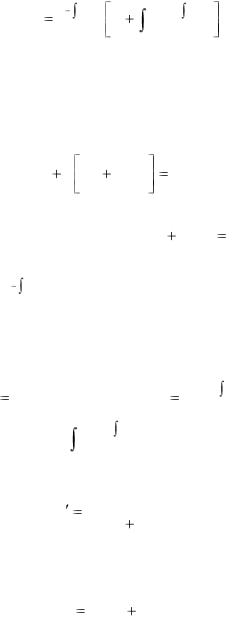
y(x) e |
a(x)dx C |
b(x)e a(x)dx . |
(5.3)
Чаще используется метод И. Бернулли. В этом случае решение находят в виде у(х) = u(x)v(x). Подставляя в уравнение, получим
|
|
v |
du |
u |
|
dv |
|
a(x)v |
b(x). |
|
|||||
|
|
dx |
|
dx |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Выберем теперь v так, чтобы |
|
|
dv |
a(x)v |
0, |
||||||||||
|
|
|
|
|
|||||||||||
|
|
dx |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
т.е. выбираем функцию |
|
|
|
|
|
|
|
|
|
|
|
||||
v(x)= |
e a(x)dx |
- |
|
|
как |
|
решение |
однородного |
|||||||
уравнения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функцию u(х) определяем из оставшегося уравнения |
|||||||||||||||
v |
du |
b(x), |
|
|
|
|
т.е. |
|
|
du |
b(x)e a(x)dx . |
||||
dx |
|
|
|
|
|
|
dx |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Откуда, u(х) = С + |
b(x)e a(x)dx . Перемножая функции |
||||||||||||||
u(х) и v(x), приходим к (5.3). |
|
|
|
|
|
|
|
||||||||
Нелинейное уравнение |
|
|
|
|
|
|
|||||||||
|
|
|
|
y |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p(y)x |
q(y) |
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
сводится к линейному, если переменную х рассматривать как функцию аргумента у:
dx |
p(y)x q(y). |
|
|
||
dy |
||
|
К линейным приводятся и уравнения вида

у'+а(х)у = b(x)yn, |
(n 0,1) |
называемые уравнениями Бернулли. Достаточно сделать замену х = у1-n. Однако решение уравнения Бернулли удобнее искать в виде у = uv, не приводя к линейному.
Уравнение Рикатти
у'+ а(х) у + b(х) у2 = с(х)
вобщем случае не интегрируется в квадратурах. Но если известно одно частное решение у = у(х), то заменой у = у + z уравнение Риккати сводится к уравнению Бернулли. Частное решение иногда можно подобрать, исходя из
вида свободного члена уравнения.
Например, для уравнения у'+у=2/х2 будем искать у
ввида у=k/х. Подставляя в уравнение, находим k=-1 и k=2. Замена у = z-1/х приводит исходное уравнение к
уравнению Бернулли |
z |
2 |
z |
z2 .Окончательно, |
|||||||
|
|||||||||||
|
|
|
|
|
|
|
|
x |
|
||
|
y |
|
2cx3 |
1 |
|
|
|
|
|
||
|
|
(cx3 |
1)x |
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
и y |
2 |
|
– особое |
решение, |
существование которого |
||||||
|
|
||||||||||
x |
|||||||||||
|
|
|
|
|
|
|
|
|
|||
является следствием нарушения непрерывности в правой части уравнения при х=0.
Пример 1. Решить уравнение
dy |
1 |
. |
|
|
|
|
|
dx |
x cos y sin 2 y |
||
Р е ш е н и е. Данное уравнение является линейным, если рассматривать x как функцию от y

dx |
x cos y sin 2 y |
|
|
||
dy |
||
|
Ищем общее решение данного уравнения в виде x u(y)v(y)
Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
v |
du |
|
u |
du |
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
dy |
|
dy |
|
dy |
||||||
Подставляя x и |
dx |
|
в уравнение, найдѐм |
||||||||||||
|
|||||||||||||||
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
v |
du |
u |
dv |
|
v cos y |
|
sin 2 y . |
|||||||
|
dy |
dy |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Функцию v (y) найдѐм из условия |
|
|
|
||||||||||||
|
|
|
|
|
|
dv |
v cos y |
|
0 . |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
dy |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Берѐм любое частное решение этого уравнения,
например, v( y) |
esin y , тогда |
|
|||
|
e |
sin y du |
sin 2 y . |
||
|
|
dy |
|
||
|
|
|
|
||
Откуда |
|
|
|
|
|
u |
e sin y sin 2 ydy |
2e sin y 1 sin y c . |
|||
Следовательно, общим решением будет функция

|
|
x cesin y |
2 sin y |
2 . |
|
|
|
||
Пример 2. Решить уравнение Бернулли: |
|
||||||||
|
|
xy |
y |
y 2 ln x . |
|
|
|
||
Р е ш е н и е. Положим y |
u(x)v(x) . Тогда будем иметь |
||||||||
|
xvu |
u xv |
v |
u 2 v 2 ln x . |
|
|
|
||
Функцию v(x) найдѐм как частное решение |
|||||||||
уравнения |
xv v |
0 . |
Имеем |
v x |
1 |
|
. Тогда |
||
x |
|||||||||
|
|
|
|
|
|
|
|||
uu 2 ln x . Откуда, разделяя переменные и интегрируя, v2
получим
1 |
|
ln x |
dx |
ln x |
1 |
c , |
||||
|
|
|
|
|
|
|
||||
|
u |
|
|
x2 |
x |
x |
|
|||
таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
x |
|
. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 cx |
ln x |
|
|
|||||
Так что общее решение уравнения имеет вид
x
y 1 cx ln x .
Пример 3. Найти решение задачи Коши
y’+y=xy2 , y(0)=1.
Р е ш е н и е. Уравнение Бернулли будем интегрировать с помощью подстановки y=uv. Тогда
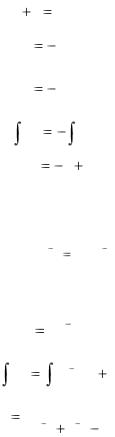
y’=u’v+uv’. И после подстановки первоначальное уравнение примет вид:
u’v + uv’ +uv = xu2v2
u’v + u(v’ +v) = xu2v2 (*)
Приравняем к нулю выражение стоящие в скобках
v' v |
0 |
|||||
dv |
v |
|||||
|
|
|
|
|
||
dx |
||||||
|
||||||
dv |
dx |
|||||
|
|
|
|
|
||
v |
||||||
|
||||||
|
dv |
dx |
||||
|
|
|
|
|
||
|
|
v |
||||
|
|
|
||||
|
|
|
||||
ln |
v |
|
x C |
|||
|
|
|
|
|
|
|
Из общего решения выберем одно частное уравнение v=e-x
Подставляя v в уравнение (*) , получим новое уравнение
du |
e x |
xu2e 2 x |
|
||
dx |
|
|
Это уравнение является уравнением с разделяющимися переменными. Решаем его
|
|
du |
xe |
x dx |
|
|
|||
|
|
|
|
|
|
|
|||
|
|
u 2 |
|
|
|||||
|
|
|
|
|
|
||||
|
du |
xe x dx |
C; |
||||||
|
|
|
|
|
|||||
|
u 2 |
||||||||
|
|
|
|
|
|||||
u |
|
|
|
1 |
|
|
|||
|
|
|
|
|
|||||
xe x |
e x |
C |
|||||||
|
|
|
|||||||
Следовательно, общее решение первоначального уравнения

e x
y xe x e x C .
Для того, чтобы найти С, воспользуемся начальным условием.
|
|
y(0) |
|
|
1 |
; |
||
|
|
|
|
|
||||
1 |
C |
|||||||
1 |
|
|
1 |
|
c 0 |
|||
|
|
|
|
|
|
|
||
1 |
C |
|
|
|
||||
|
|
|
|
|
||||
Окончательное решение задачи Коши |
||||||||
y |
|
|
e x |
|
|
|
||
xe |
x |
|
|
e |
x |
|
||
|
|
|
|
|||||
Или после сокращения на e |
x |
|
получим |
|||||
1
y x 1 .
1.6 Уравнения в полных дифференциалах
Уравнение
М(х,у)dх + N(x,y)dy = 0 |
(6.1) |
называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции U(x,y), т.е.
dU(x, y) |
U |
dx |
U |
dy M(x, y)dx N(x, y)dy. |
|
|
|||
|
x |
y |
||
