
Дифференциальные уравнения. Провоторова Е.Н
.pdf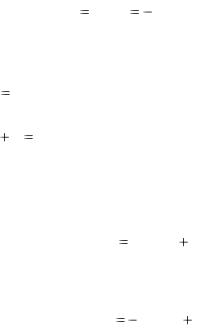
Поясним этот метод на примере. Пусть требуется проинтегрировать систему
|
|
|
|
|
|
dx |
|
y, |
dy |
|
x, |
|
|
|
(2.2). |
|
|
|
|
|
|
dt |
dt |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Дифференцируя |
первое |
уравнение |
системы, |
имеем |
||||||||
|
d 2 x |
|
dy |
, |
откуда, используя |
второе уравнение, получаем |
|||||||||
|
dt2 |
dt |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
d 2 x |
|
x 0 |
— линейное дифференциальное уравнение Его |
|||||||||||
|
dt2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
общее |
|
|
решение |
второго |
порядка |
с |
постоянными |
||||||||
коэффициентами |
с |
одной неизвестной |
функцией. |
||||||||||||
имеет |
вид |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
x(t) |
C1 cost |
C2 sint. |
|
|
|
||
|
В силу первого уравнения системы находим функцию |
||||||||||||||
|
|
|
|
|
|
|
|
y(t) |
C1 sint |
C2 cost. |
|
|
|
||
Найденные |
|
функции, |
как легко проверить, |
при |
любых |
||||||||||
значениях C1 , C2 . удовлетворяют заданной системе.
3.3 Системы линейных дифференциальных уравнений.
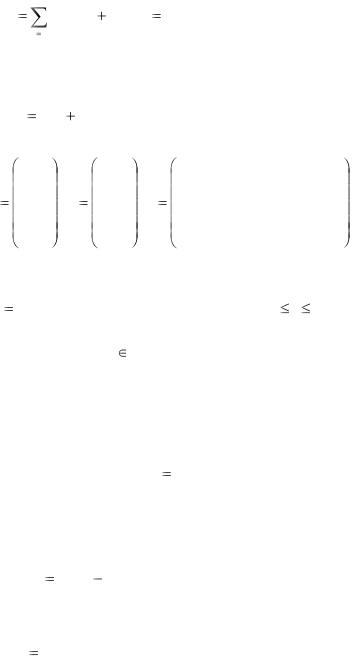
Система дифференциальных уравнений называется линейной, если она линейна относительно неизвестных функций и их производных. Система n линейных уравнений первого порядка, записанная в нормальной форме, имеет вид
|
|
|
|
dxi |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aif (t)xi |
|
|
fi (t),i 1,2,..., n, |
|
|
(3.1) |
|
|||||||
|
|
|
|
dt |
|
|
|
|
|
|
|||||||||
|
|
|
|
i |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
в матричной форме – |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
dX |
|
AX F, |
|
|
|
|
|
|
|
(3.2) |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
x1 (t) |
|
f1 (t) |
|
a11 (t) |
a12 (t) a1n (t) |
|
|
||||||
где |
|
X |
|
x2 (t) |
, F |
f2 |
(t) |
, A |
a21 (t) a22 (t) a2n (t) |
. |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
xn (t) |
|
fn (t) |
|
an1 (t) an2 (t) ann (t) |
|
|
|||||||
|
|
Теорема |
|
3.1. |
|
Если |
все |
функции |
aij (t) |
|
и |
||||||||
fi (t) , i, j 1,2,..., n, непрерывны |
на отрезке a |
t |
b , то |
в |
|||||||||||||||
достаточно |
|
|
малой |
|
|
окрестности |
каждой |
точки |
|||||||||||
M |
0 |
(t |
, x0 |
, x0 |
,..., x0 ) , где t |
0 |
(a,b) |
, выполнены условия теоремы |
|||||||||||
|
0 |
1 |
2 |
|
|
n |
|
|
|
|
|
|
|
|
|||||
существования и единственности решения задачи Коми и, следовательно, через каждую такую точку проходит единственная интегральная кривая системы (3.1).
Действительно, в таком случае правые части системы (3.1) непрерывны по совокупности аргументов t, x1, x2 ,..., xn и
частные производные по xj , j 1,2,..., n ограничены, так как
эти производные равны непрерывным на отрезке [a, b] коэффициентам aij (t) .
Введем линейный оператор
L d / dt A .
Тогда система (3.2) коротко запишется в виде
L[X ] F. |
(3.3) |

Если матрица F — нулевая, т. е. fi (t) 0,i 1,2,..., n, на
интервале (а, b), то система (3.1) называется линейной однородной и имеет вид
L[X ] 0. |
(3.4) |
Приведем некоторые теоремы, устанавливающие свойства решений линейных систем.
Теорема 3.2. Если X(t) является решением линейной однородной системы L[X] = 0, то сХ(t), где с — произвольная постоянная, является решением той же системы.
Теорема 3.3. Сумма X1(t) X 2 (t) двух решений X1 (t) u X 2 (t) однородной линейной системы уравнений является решением той же системы.
|
|
|
|
|
|
m |
|
Следствие. |
Линейная |
комбинация |
ci Xi (t) с |
||||
|
|
|
|
|
|
i 1 |
|
произвольными |
постоянными |
коэффициентами |
ci |
решений |
|||
X1 (t),..., X m (t) |
линейной |
|
однородной |
|
системы |
||
дифференциальных уравнений |
L[X ] 0 |
является решением |
|||||
той же системы. |
|
|
~ |
|
|
|
|
Теорема |
3.4. |
Если |
|
решение |
линейной |
||
X (t) есть |
|||||||
неоднородной системы L[X ] F , а X 0 (t) — решение соответствующей однородной системы L[X ] 0, то сумма
~ |
|
|
|
|
|
X (t) X 0 |
(t) будет решением неоднородной системы |
|
|||
|
|
L[X ] |
F . |
|
|
|
|
|
|
~ |
|
Действительно, |
по |
условию, |
L[ X ] F, F[ X 0 |
] 0 . |
|
Пользуясь свойством аддитивности оператора L, получаем |
|||||
|
~ |
~ |
|
|
|
|
L[ X X 0 ] |
L[ X ] L[ X 0 ] |
F. |
|
|

Это означает, что сумма |
~ |
(t) есть решение |
X (t) X 0 |
||
неоднородной системы уравнений L[X ] |
F . |
|
Определение . Векторы X1 (t), X 2 (t),..., X n (t)
x1k (t) |
|
|
x2k |
(t) |
|
X k |
|
, |
xnk (t)
называются линейно зависимыми на интервале a
существуют постоянные числа |
1, 2 ,..., n |
что |
|
, где
tb , если такие,
1 X1(t) 1 X1(t) ... 1 X1(t) 0 |
(3.5) |
при t (a,b) , причем по крайней мере одно из чисел |
i не |
равно нулю. Если тождество (3.5) справедливо только при
1 |
2 |
... |
n |
0 , |
то |
векторы |
X1 (t), X 2 (t),..., X n (t) |
называются линейно независимыми на (a,b) . |
|||||||
|
Заметим, что одно векторное тождество (3.5) |
||||||
эквивалентно n тождествам: |
|
|
|||||
|
|
n |
|
|
|
|
|
|
|
|
k x1k (t) |
0, |
|
|
|
|
k |
1 |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
k x2k (t) |
0, |
|
|
(3.5’) |
|
k |
1 |
|
|
|
|
|
|
.......... .......... .... |
|
|
|
|||
|
|
n |
|
|
|
|
|
|
|
|
k xnk (t) |
0. |
|
|
|
|
k |
1 |
|
|
|
|
|
Определитель

|
x11 (t) |
x12 (t) x1n (t) |
|
|
W (t) |
x21 (t) |
x22 (t) x2n (t) |
|
|
|
|
|
|
|
|
|
|||
|
xn1 (t) xn2 (t) xnn (t) |
|
||
называется определителем |
Вронского системы векторов |
|||
X1 (t), X 2 (t),..., X n (t) .
Определение . Пусть имеем линейную однородную систему
|
|
|
|
|
dX |
A(t) X , |
|
|
|
|
(3.6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
dt |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где A(t) |
|
— n n -матрица |
с элементами |
aij (t) . Система |
n |
||||||||
решений |
|
X1 (t), X 2 (t),..., X n (t) |
линейной однородной системы |
||||||||||
(3.4), линейно независимых на интервале a |
t b , называется |
||||||||||||
фундаментальной. |
|
|
|
|
|
|
|
|
|||||
Теорема3.5. |
Определитель |
Вронского |
W (t) |
||||||||||
фундаментальной на |
интервале |
a |
t |
b |
системы решений |
||||||||
линейной однородной системы (3.4) с непрерывными |
на |
||||||||||||
отрезке |
a |
t |
b коэффициентами |
aij (t) отличен от нуля во |
|||||||||
всех точках интервала (a,b) . |
|
|
|
|
|
|
|
||||||
Теорема 3.6. (о структуре общего решения линейной |
|||||||||||||
однородной системы). Общим решением в области a |
t |
b , |
|||||||||||
| xk | |
, |
k |
1,2,..., n , линейной однородной системы |
|
|
||||||||
|
dX |
|
A(t) X |
|
|
|
|
|
|
(3.7) |
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
dt |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
с непрерывными на отрезке |
a |
t |
b |
коэффициентами aij (t) |
|||||||||
является линейная комбинация n линейно независимых на интервале a t b решений X1 (t), X 2 (t),..., X n (t) системы
(3.7):
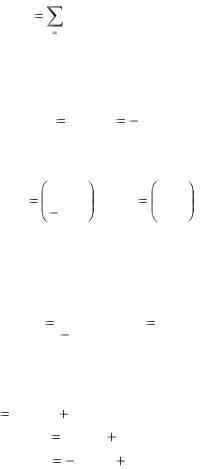
n |
|
X 0,0 |
ci Xi (t) |
i |
1 |
( c1, c2 ,..., cn — произвольные постоянные числа). Например, система
dx1 |
x2 , |
dx2 |
x1 |
dt |
dt |
имеет, как нетрудно проверить, решения
X1(t) |
cost |
, X 2 (t) |
sint . |
|
sint |
|
cost |
Эти решения линейно независимы, так как определитель Вронского отличен от нуля:
W (t) |
cost |
sint |
1. |
|
sint |
cost |
|||
|
|
|||
|
|
|
|
Общее решение системы имеет вид
X (t) c1 X1(t) |
c2 X2 (t) |
или |
x1(t) |
c1 cost |
c2 sint, |
x2 (t) |
c1 sint |
c2 cost |
( c1,c2 — произвольные постоянные).
Квадратная матрица
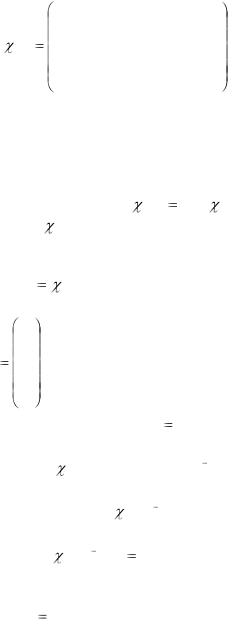
|
x11 (t) |
x12 (t) x1n (t) |
|
||
(t) |
x21 (t) |
x22 (t) x2n (t) |
, |
||
|
|
|
|||
|
|
||||
|
xn1 (t) |
xn 2 (t) xnn (t) |
|
||
столбцами которой являются линейно независимые решения X1 (t), X 2 (t),..., X n (t) системы (3.7), называется
фундаментальной матрицей этой системы. Нетрудно проверить, что фундаментальная матрица удовлетворяет матричному уравнению d / dt A(t) (t) .
Если (t) — фундаментальная матрица системы (3.7), то общее решение системы можно представить в виде
|
X (t) |
(t)C, |
(3.8) |
|
|
c1 |
|
|
|
где C |
c2 |
-постоянная матрица-столбец с произвольными |
||
|
||||
|
|
|
||
|
cn |
|
|
|
элементами. Полагая в (3.8) t |
t0 , имеем |
|||
X (t0 ) 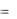 (t0 )C , откуда C
(t0 )C , откуда C 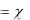 1(t0 ) X (t0 ) ;
1(t0 ) X (t0 ) ;
следовательно, X (t) 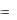 (t)
(t)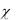 1(t0 )X (t0 ) .
1(t0 )X (t0 ) .
Матрица (t)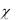 1(t0 ) K(t,t0 ) называется матрицей Коши. С ее помощью решение системы (3.7) можно представить так:
1(t0 ) K(t,t0 ) называется матрицей Коши. С ее помощью решение системы (3.7) можно представить так:
X (t) K (t,t0 ) X (t0 ).
Теорема 3.7 (о структуре общего решения линейной
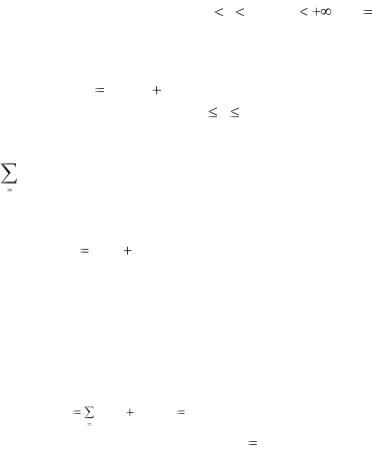
неоднородной системы дифференциальных уравнений).
Общее решение в области |
a t b , |
| xk | |
, k 1,2,..., n , |
линейной неоднородной |
системы |
дифференциальных |
|
уравнений |
|
|
|
|
dX / dt |
A(t)X F(t) |
|
|
(3.2) |
||||
с непрерывными на отрезке a |
t |
b коэффициентами aij (t) и |
|||||||
правыми частями |
fi (t) |
равно |
сумме общего решения |
||||||
n |
|
|
|
|
|
|
|
||
ck X k (t) |
соответствующей однородной системы и какого- |
||||||||
k 1 |
|
|
|
~ |
|
|
|
||
нибудь частного решения |
|
|
|
||||||
X (t) неоднородной системы (3.2): |
|||||||||
|
X о.н. |
|
X о.о |
X ч.н . |
|
|
|
|
|
3.4. |
|
Системы |
линейных |
дифференциальных |
|||||
уравнений с постоянными коэффициентами |
|||||||||
Рассмотрим |
линейную |
систему |
дифференциальных |
||||||
уравнений |
|
|
|
|
|
|
|
||
|
dxi |
n |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
aij xi |
f i (t), i |
1,2,...,n, |
|
|
|
|
dt |
|
|
|
|||||
|
i |
1 |
|
|
|
|
|
||
в которой все коэффициенты aij (i, j 1,2,..., n) — постоянные.
Проще всего такая система |
интегрируется сведением ее к |
одному уравнению более |
высокого порядка, причем |
это уравнение будет также линейным с постоянными коэффициентами. Другой эффективный метод интегрирования систем с постоянными коэффициентами — метод преобразования Лапласа.
Мы рассмотрим еще метод Эйлера интегрирования линейных однородных систем дифференциальных уравнений с постоянными коэффициентами. Он состоит в следующем. Будем искать решение системы
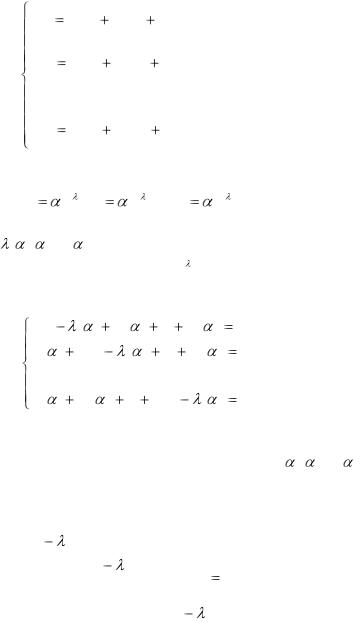
|
dx1 |
|
|
a11x1 |
a12 x2 |
...a1n xn , |
|
|
|
dt |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
dx2 |
|
|
a21x1 |
a22 x2 |
...a2n xn |
, |
|
|
dt |
|
|
(4.1) |
||||
|
|
|
|
|
|
|
||
|
|
|
||||||
|
dxn |
|
|
an1x1 |
an 2 x2 |
...ann xn |
|
|
|
dt |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
в виде
x |
e t , x |
|
2 |
e t ,..., x |
n |
e t , |
(4.2) |
|
1 |
1 |
2 |
n |
|
|
|||
где , 1, |
2 ,..., |
n |
— постоянные. Подставляя xk |
в форме (4.2) |
||||
в систему (4.1), сокращая на e t и перенося все члены в одну часть равенства, получаем систему
(a11 |
|
) 1 |
a12 |
2 ... |
a1n |
n |
0, |
|
|
a21 |
1 |
(a22 |
) |
2 ... |
a2n |
n |
0, |
(4.3) |
|
|
|||||||||
|
|||||||||
an1 |
1 |
an2 2 |
... |
(ann |
) |
n |
0, |
|
|
Для того чтобы эта система (4.3) линейных однородных алгебраических уравнений с n неизвестными 1, 2 ,..., n
имела нетривиальное решение, необходимо и достаточно, чтобы ее определитель был равен нулю:
a11 |
a12 |
a1n |
|
|
a21 |
a22 |
a2n |
0. |
(4.4) |
|
|
|
||
an1 |
an 2 |
ann |
|
|
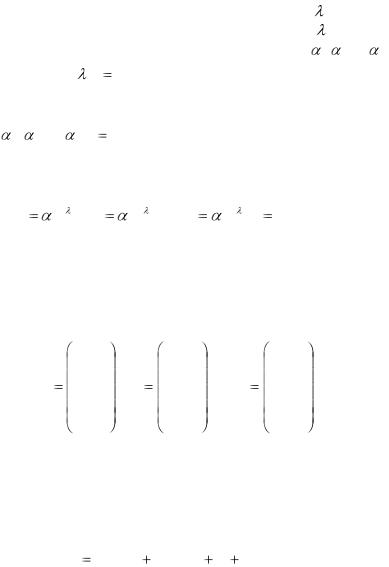
Уравнение (4.4) называется характеристическим. В его
левой части стоит многочлен относительно |
|
степени n. Из |
этого уравнения определяются те значения |
, |
при которых |
система (4.3) имеет нетривиальные решения |
1, |
2 ,..., n . Если |
все корни i ,i 1,2,..., n характеристического уравнения (4.4) различные, то, подставляя их по очереди в систему (4.3),
находим |
соответствующие |
им нетривиальные решения |
1i , 2i ,..., |
ni ,i 1,2,..., n , этой |
системы и, следовательно, |
находим n решений исходной системы дифференциальных уравнений (4.1) в виде
x |
1i |
e i t , x |
2i |
e i t ,..., x |
ni |
e i t ,i 1,2,..., n, |
(4.5) |
1i |
2i |
ni |
|
|
где второй индекс указывает номер решения, а первый — номер неизвестной функции. Построенные таким образом решений линейной однородной системы (4.1)
x11 (t) |
|
x12 (t) |
|
x1n (t) |
|
|
x21 |
(t) |
, X 2 |
x22 (t) |
,..., X1 |
x2n (t) |
|
X1 |
|
|
|
(4.6) |
||
|
|
|
|
|
||
xn1 (t) |
|
xn2 (t) |
|
xnn (t) |
|
|
образуют, как можно проверить, фундаментальную систему решений этой системы.
Следовательно, общее решение однородной системы дифференциальных уравнений (4.1) имеет вид
X (t) c1 X1 (t) c2 X 2 (t) ... cn X n (t),
или
