
Дифференциальные уравнения. Провоторова Е.Н
.pdfСлучай 1. Правая часть (5.1) имеет вид f(х) = Рn(х)еах, где
α € R, Рn(х) — многочлен степени n. Уравнение (5.1)
запишется в виде
y′′+ py′ + qy = Рn(х) eαx
В этом случае частное решение у* ищем в виде:
у* = хrQn(х)eαx,
где г — число, равное кратности а как корня характеристического уравнения k2 +pk + q = 0 (т.е. г — число, показывающее, сколько раз а является корнем уравнения k2+pk + q =0 ), a.Qn(x) = А0хn + A1xn-1 + … +An
— многочлен степени n, записанный с неопределенными коэффициентами Ai (i = 1,2,...,n).
Случай 2: правая часть (5.1) имеет вид
f(x) = eαx(Рn(х) cosβx + Qm(x)sinβx), где Рn(х) и Qm(x) -
многочлены степени n, m соответственно, α и β действительные числа. Уравнение (5.1) запишется в виде
y′′+ py′ + qy = eαx(Рn(х) cosβx + Qm(x)sinβx)
в этом случае частное решение у*нужно искать в виде
у* = хreαx(Ml(х) cosβx + N l(x)sinβx)
где r – число, равное кратности α + βi как корня характеристического уравнения к2+ pк + q =0 Ml (х) и Nl(x) – многочлены степени l c неопределѐнными коэффициентами, l – наивысшая степень многочленов Рn(х) и Qm , т.е. l = max(n, m).
Пример1. Найти частное решение уравнения
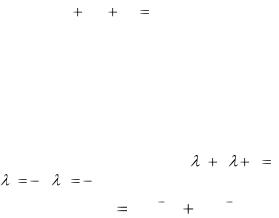
y′′+ 2y′ + y= cosx
Решение. Характеристическое уравнение
k2 +2k + 1 = 0
имеет корни k1 = k2 = - 1 .В данном случае числа a±βi=± i не являются корнями характеристического уравнения, значит частное решение следует искать в виде
у* = M cosx + N sin x, |
|
|
|
|
Подставляя функцию |
у* |
в |
уравнение |
и |
приравнивая коэффициенты |
отдельно |
при |
косинусах |
и |
при синусах , находим М=0, N=0,5, следовательно, у*
= 0,5 sin x .
Пример2. Найти общее решение дифференциального уравнения
y 4y
4y 3y x
3y x
Решение.
Это неоднородное линейное уравнение второго порядка с постоянными коэффициентами. Решение
такого уравнения состоит из |
двух частей y - общего |
решения соответствующего |
однородного уравнения и |
y* - частного решения исходного уравнения.
Характеристическое уравнение |
2 |
|
4 3 |
0 имеет |
||||
|
|
|||||||
корни |
1 |
3, 2 |
1. |
Значит, |
общее |
решение |
||
однородного уравнения y |
C e 3x |
C |
2 |
e x . |
|
|||
|
|
|
|
1 |
|
|
|
|
Для нахождения частного решения неоднородного уравнения воспользуемся методом неопределѐнных коэффициентов. Будем искать частное решение в виде
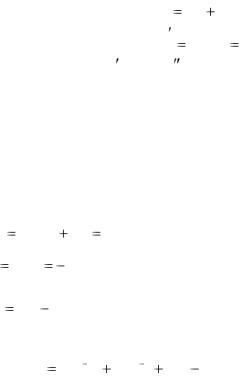
y* Ax B.
y* A; y*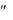 0.
0.
Подставим y* , y* и y* в исходное уравнение и получим
4А+3(Аx+B)=x.
Приравнивая коэффициенты при одинаковых степенях х, будем иметь
3A |
|
x1 ,4 A 3B 0. |
||||||
A |
1 |
, B |
|
4 |
|
|||
3 |
9 |
|
||||||
|
|
|
|
|||||
y* |
|
1 |
x |
4 |
. |
|
||
3 |
9 |
|
||||||
|
|
|
|
|
||||
Следовательно, общее решение уравнения имеет вид
y C e 3x |
C |
e x |
1 |
x |
4 |
. |
|
|
|||||
1 |
2 |
3 |
9 |
|
||
|
|
|
||||
Пример 3.Найти вид частного решения уравнения
y′′-2 y′+у =х ex
Решение. Характеристическое уравнение k2 - 2k + 1
= 0
имеет корни условию k1 = k2 = 1 . В данном случае число a=1 является двукратным корнем характеристического уравнения, значит частное решение следует искать в виде
у* = хr eαx(Ах+В).

2.6.Уравнения Эйлера
Уравнения вида
a |
0 |
xn y(n) |
a xn 1 y(n 1) |
... a |
n 1 |
xy |
a |
n |
y 0, |
(6.1) |
|
|
1 |
|
|
|
|
|
где все ai постоянные, называются уравнениями Эйлера. Эти уравнения заменой независимого
переменного
x et
преобразуются в линейные однородные уравнения с постоянными коэффициентами:
b y (n) |
... b |
y |
t |
b y(t) 0. |
0 t |
n 1 |
|
n |
|
|
(6.2) |
|
|
|
З а м е ч а н и е 1. Уравнения вида
a |
0 |
(ax b)n y(n) |
a (ax b)n 1 |
y(n 1) |
|
|
1 |
|
|
... an 1 (ax b) y |
an y 0 |
(6.3) |
||
также называются уравнениями Эйлера и сводятся к линейным однородным уравнениям с постоянными коэффициентами заменой переменных
ax b et .
З а м е ч а н и е 2. Частные решения уравнения (6.1) можно сразу искать в виде
y x k ,
при этом для k мы получаем уравнение, которое совпадает с характеристическим уравнением для уравнения (6.2).
Пример. Найти общее решение уравнения Эйлера
|
|
|
|
|
|
|
|
|
x 2 y |
2xy |
|
|
6 y |
0 . |
|
|
|
|
|
|
|
|||||||||||||
|
Решение. Делаем в уравнении подстановку x et , |
|||||||||||||||||||||||||||||||||
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
t dy |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
dt |
|
|
e |
, |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
dx |
|
|
|
|
dt |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
dy |
|
|
d 2 y |
|
|
|
|
dy |
e |
t |
|
|
|
|
|
|
|
||||||||||||
|
|
dy |
|
|
|
|
|
|
|
|
|
dt |
2 |
|
|
|
|
|
dt |
|
|
|
|
|
2t d 2 y |
|
dy |
|||||||
y |
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
e |
|
||||||||||||||||||
|
dx |
|
|
|
dx |
|
|
|
|
|
|
|
|
et |
|
|
|
|
|
|
dt |
2 |
|
dt |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
и уравнение примет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
d 2 y |
|
|
dy |
|
|
6y |
0. |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
dt 2 |
|
|
dt |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Корни характеристического уравнения: 1= -3, 2=2, и общим решением последнего уравнения будет функция: y C1e 3t C2 e2t .
Но, так как x et , то
y C x 3 |
C |
x 2 |
или |
1 |
2 |
|
|

yC1 C2 x2 . x3
3.Системы дифференциальных уравнений.
3.1.Основные понятия и определения.
Системой дифференциальных уравнений называется совокупность дифференциальных уравнений, каждое из которых содержит независимую переменную,
функцию и ее производные. |
|
|
|
Система |
m дифференциальных уравнений с m |
||
неизвестными |
называется канонической , если она |
||
разрешена относительно старших производных. |
|
||
Система |
уравнений |
первого |
порядка, |
разрешенных относительно производных от искомых функций,
xi fi (t, x1, x2 ,..., xn ),i 1,2,..., n , |
(1.1) |
называется нормальной.
Если в канонической системе, содержащей производные произвольного порядка
xi(ki )  fi (t, x1, x1,..., x1(k1 1) ,..., xm , xm , xm(km 1) ) ,
fi (t, x1, x1,..., x1(k1 1) ,..., xm , xm , xm(km 1) ) ,
принять xi , xi ,..., xiki 1 за новые вспомогательные функции,
то общую каноническую систему (1.2) можно заменить эквивалентной ей нормальной системой, состоящей из

N k1 |
k2 |
... |
km |
уравнений. |
Поэтому |
достаточно |
рассматривать лишь нормальные системы. |
|
|||||
|
Например, одно уравнение d 2 x / dt2 |
x является |
||||
частным |
случаем |
канонической |
системы. |
Положив |
||
dx/ dt |
y , |
в |
силу |
исходного уравнения будем иметь |
||
dy / dt |
x . В результате получаем нормальную систему |
|||||
уравнений |
|
dx / dt |
y, |
dy / dt |
x, |
эквивалентную исходному уравнению.
Определение . Решением нормальной системы (1.1) на интервале (a,b) изменения аргумента t называется всякая система n функций
(t), |
n |
x |
n |
(t),...,x |
2 |
x |
2 |
x(t),x |
x |
|
|
|
|
1 |
1 |
(1.2)
дифференцируемых на интервале a t b , обращающая уравнения системы (1.1) в тождества по t на интервале
(а,b).
Задача Коши для системы (1.1) формулируется так: найти решение (1.2) системы при начальных условиях
x | |
x0 |
, x | |
x0 |
,..., x | |
x0. |
1 t t0 |
1 |
2 t t0 |
2 |
n t t0 |
n |
(1.3)
Теорема 1 (существования и единственности решения задачи Коши). Пусть имеем нормальную систему дифференциальных уравнений
xi |
f i (t, x1 , x2 ,...,xn ), i 1,2,...,n |
(1.1) |

и пусть функции fi (t, x1, x2 ,..., xn ),i 1,2,..., n определены в некоторой (n+1)-мерной области D изменения переменных t, x1, x2 ,..., xn . Если существует окрестность
 точки M0 (t0 , x10 , x20 ,..., xn0 ) , в которой функции fi непрерывны по совокупности аргументов и имеют
точки M0 (t0 , x10 , x20 ,..., xn0 ) , в которой функции fi непрерывны по совокупности аргументов и имеют
ограниченные |
частные производные |
по |
переменным |
x1, x2 ,..., xn , то |
найдется интервал |
t0 |
h0 t t0 h0 |
изменения t, на котором существует единственное решение нормальной системы (1.1), удовлетворяющее начальным условиям (1.3).
Определение. Система n функций
xi xi (t,C1,C2 ,..., Cn ),i 1,2,..., n (1.4)
зависящих от t и n производных постоянных C1,C2 ,..., Cn ,
называется общим решением нормальной системы (1.1) в некоторой области существования и единственности решения задачи Коши, если
1)при любых допустимых значениях C1,C2 ,..., Cn система функций (1.4) обращает уравнения (1.1) в тождества,
2)в области  функции (1.4) решают любую
функции (1.4) решают любую
задачу |
Коши. |
|
|
Решения, получающиеся из общего при |
|||
конкретных |
значениях |
постоянных |
C1,C2 ,..., Cn , |
называются частными решениями.
Обратимся для наглядности к нормальной системе двух уравнений:
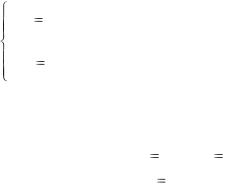
|
|
dx1 |
|
f1 (t, x1, x2 ), |
|
|
dt |
|
|
|
|
|
|
|
|
|
dx2 |
|
f2 (t, x1, x2 ), |
|
|
dt |
|
|
|
|
|
|
|
(1.5) |
|
|
|
Будем рассматривать систему значений |
t, x1, x2 |
как прямоугольные декартовы координаты точки |
|||
трехмерного пространства, отнесенного к системе
координат 0tx1x2 . Решение x1 |
x1(t), x2 x2 (t) |
системы |
||||
(1.5), принимающее при |
t t |
0 |
значения |
x0 |
, x0 |
, |
|
|
|
1 |
2 |
|
|
определяет в пространстве некоторую линию, проходящую через точку M0 (t0 , x10 , x20 ) . Эта линия через
данную точку M0 (t0 , x10 , x20 ) . Теорема 1 устанавливает существование и единственность такой кривой.
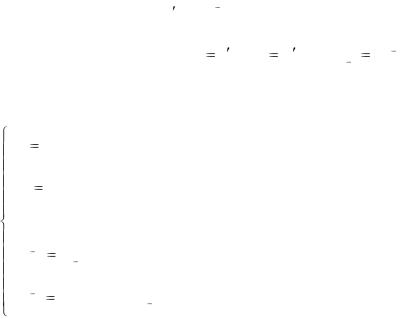
3.2. Интегрирование нормальных систем
Один из методов интегрирования — метод исключения. Частным случаем канонической системы является одно уравнение n-го порядка, разрешенное относительно старшей производной,
x(n) 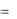 f (t, x, x ,..., x(n 1) ).
f (t, x, x ,..., x(n 1) ).
Введя новые функции x1 x (t), x2 x (t),..., xn 1 x(n 1) (t) ,
(t),..., xn 1 x(n 1) (t) ,
заменим это уравнение следующей нормальной системой n уравнений:
|
dx |
|
|
x1, |
|
|
||
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|||
|
|
|
|
|
|
|||
|
dx1 |
|
|
|
x2 , |
|
|
|
|
dt |
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
(2.1) |
|||
|
dxn |
2 |
|
xn 1 |
, |
|
||
|
dt |
|
|
|
||||
|
|
|
|
|
|
|||
|
dxn |
1 |
|
f (t, x, x1 |
,..., xn 1 ), |
|||
|
dt |
|
|
|||||
|
|
|
|
|
|
|||
одно уравнение n-го порядка эквивалентно нормальной системе (2.1).
Можно утверждать и обратное, что, вообще говоря, нормальная система n уравнений первого порядка (1.1) эквивалентна одному уравнению порядка n. На этом и основан метод исключения для интегрирования систем дифференциальных уравнений.
