Учебное пособие 1561

Е.Н.Провоторова

ДИФФЕРЕНЦИАЛЬНЫЕ

УРАВНЕНИЯ

Воронеж 2003

MИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Воронежский государственный технический университет

Е.Н.Провоторова

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Утверждено Редакционно-издательским советом университета в качестве учебного пособия.

Воронеж 2003

УДК 517.9

Дифференциальные уравнения: Учеб.пособие. Е.Н.Провоторова . Воронеж: Воронеж. гос. техн. ун-т,

2003. 98 с.

В пособии содержатся основные теоретические сведения по дисциплине "Дифференциальные уравнения" и примеры интегрирования наиболее важных классов

специальностей 075500 «Комплексное обеспечение

обучения.Учебное пособие подготовлено на магнитном

Провоторова Е.Н., 2003 Воронежский государственный технический университет, 2003

ВВЕДЕНИЕ

Дифференциальные уравнения занимают особое место в ряду математических дисциплин в силу многочисленных приложений в практических задачах. При изучении физических явлений часто не удается непосредственно найти закон, связывающий независимую переменную и функцию, описывающую процесс, но можно установить связь между этой функцией и ее производной, характеризующей скорость течения процесса. Эта связь и выражается дифференциальным уравнением.

Первые задачи, приводящие к дифференциальным уравнениям, исследовались в трудах Ньютона и Лейбница. В 18 веке тeория дифференциальных уравнений выделилась в самостоятельную математическую дисциплину. Ее успехи связаны с именами братьев Иоганна и Якоба Бернулли, Ж. Лагранжа и особенно Л. Эйлера. На первых этапах развития теории дифференциальных уравнений ученые занимались разработкой методов интегрирования дифференциальных уравнений и поисками классов уравнений, интегрируемых в квадратурах, т.е. уравнений, решения которых могут быть в явной или в неявной форме выражены через элементарные функции и интегралы от них. В середине 19 века было доказано, что в квадратурах разрешимо лишь небольшое число классов

дифференциальным уравнениям характеризовать свойства решений, а также численные методы.

В данном пособии рассматриваются основные классы дифференциальных уравнений, допускающих интегрирование в квадратурах.

1.Дифференциальные уравнения первого порядка

1.1Задачи, приводящие к дифференциальным уравнениям.

Дифференциальные равнения являются математической моделью многочисленных физических, химических, биологических и др. процессов. При составлении дифференциальных уравнений весьма часто используют физические законы, которые описывают соотношение между величинами, характеризующими изучаемый процесс, и скоростью изменения этих величин. Например, в механике – законы Ньютона, в теории электрических цепей – законы Кирхгоффа, в теории скоростей химических реакций – закон действия масс и т.д. Если физический закон протекания процесса неизвестен, то для составления дифференциального уравнения прибегают к гипотезе о линейности процесса ―в малом‖, т.е., например, считают, что в течение малого промежутка времени ∆t участвующие в процессе величины изменяются с постоянной скоростью. Составляют соотношения между приращениями этих величин и, переходя к пределу при ∆t → 0, получают уравнение, содержащее производную по времени. Дифференциальное уравнение – это как бы ―мгновенный снимок процесса‖ в данный момент времени, интегрируя дифференциальное уравнение, мы по мгновенным снимкам восстанавливаем течение процесса в целом.

Задача 1. Пусть в резервуаре имеется a кг водного раствора соли, в котором содержится b кг соли. В определенный момент включается устройство, непрерывно подающее в резервуар с кг чистой воды в секунду и одновременно удаляющее из него ежесекундно с кг раствора. При этом в самом резервуаре жидкость непрерывно перемешивается. Как изменяется количество соли в резервуаре?

Примем за начало отсчета момент t. Пусть y(t) – искомая функция, выражающая в каждый момент времени t количество соли в резервуаре. В силу условия задачи и соглашения об отсчете времени,y(0)=b. За малый промежуток [t, t+ t] из резервуара с раствором выльется (y(t)-(y(t+ t))) кг соли. Так как концентрация в

причем неравенства являются строгими, если c 0, b 0,

Исходя из характера рассматриваемого процесса, можно заключить, что y(t) – непрерывна, значит,

lim y(t Δt) y(t).

Δt 0

В результате получаем

т. е. y(t) удовлетворяет дифференциальному уравнению

Полученная формула показывает, что процесс опреснения раствора в резервуаре происходит по экспоненциальному закону.

Таким образом, дифференциальное уравнение, моделируя процесс, описывает эволюцию процесса, показывает характер происходящих с материальной системой изменений. При этом не обязательно изменения происходят во временном промежутке.

Задача 2. При определении давления воздуха над уровнем моря в зависимости от высоты p(h) поступают следующим образом. Рассматривают два горизонтальных сечения столба воздуха на высоте h и h+ h, опирающегося на площадку размером 1м2. Давление на высоте h+ h будет меньше на величину p, равную весу воздуха в столбе между двумя сечениями: p=d h, где d

– вес одного кубометра воздуха при давлении p. Полагая, что во всех сечениях между h и h+ h давление постоянно в силу закона Бойля – Мариотта, получают d=kp, где k – коэффициент пропорциональности. Выполняя деление на

Приведем еще один пример использования физического закона при составлении дифференциального уравнения.

Пусть требуется узнать, за какое время упадет на поверхность Луны камень с высоты h. Пусть x(t) – высота камня над поверхностью в момент времени t. Согласно закону свободного падения, открытому г. Галилеем, все тела, независимо от их массы, падают в поле силы тяжести с постоянным ускорением a, (для поверхности луны а=1/6g), а следовательно, х(t)= –а. Интегрируя дважды, находим

x(t) 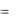at 2 /2 C1t C2 .

Постоянные С1, С2 находим из условий х (0)=0, и х(0)=h. Функция х(t) = h-at2/2 описывает закон движения камня. Моменту удара t камня о поверхность соответствует

x(t)=0, поэтому ответ задачи t 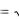2h/a .

1.2.Основные понятия теории дифференциальных уравнений.

Обыкновенным дифференциальным уравнением называется уравнение, в котором неизвестной является функция одного независимого переменного, причем в уравнения входят производные различных порядков. В самом общем виде обыкновенное дифференциальное уравнение может быть записано так:

F(x, y , y ,....y (n) ) 0.

Порядок старшей производной, входящей в состав уравнения, называется порядком уравнения. Решением уравнения (2.1) называется функция у=ф(х), обращающая это уравнение в тождество. График решения на плоскости ХОУ называется интегральной кривой, процесс нахождения решений – интегрированием дифференциального уравнения.

Уравнение 1-го порядка, разрешенное относительно производной, входящей в состав уравнения, может быть записано в виде

где f(t,x) – известная функция, определенная в некоторой области D плоскости t,x. Уже на простейших примерах видно, что любое дифференциальное уравнение имеет бесчисленное множество решений. Описать совокупность всех решений позволяет теорема существования и единственности.

Теорема. Если функция f(t,x) и ее частная производная f/ x непрерывны в некоторой области D переменных t,x, содержащей точку (to,Xo), то существует единственное решение этого уравнения, х=ф(t), удовлетворяющее условию X(to)=Xo.

Условие X(to)=Xo называется начальным условием, а задача отыскания решения дифференциального уравнения (2.1), удовлетворяющего начальному условию

– начальной задачей или задачей Коши.

Геометрически теорема существования и единственности означает, что через каждую точку области проходит одна и только одна интегральная кривая, имеющая в каждой своей точке касательную, целиком принадлежащую области D.

Геометрическая интерпретация самого уравнения (3.1) дает поле направлений в области D, которое получается, если через каждую точку (t,x), принадлежащую области D, провести отрезок ltx малой длины с угловым коэффициентом f(t,x). Любая интегральная кривая в каждой своей точке касается отрезка ltx.

На рисункe 1 представлено поле направлений уравнения Риккати х'= t2+x2, неразрешимого в квадратурах. Рисунок 1 позволяет ясно представить, как должны выглядеть интегральные кривые.

Рис.1

Общим решением дифференциального уравнения (3.1) называется функция Х=Ф(t,C), зависящая от одной произвольной постоянной С, удовлетворяющая дифференциальному уравнению при любом С и такая, что при любом начальном условии X(to) = Хо существует значение С=Со что Х =Ф(t,Co) удовлетворяет начальному условию.

Равенство вида Ф(x,t,C)=0, неявно задающее решение, называется общим интегралом