Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 1244

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

902.72 Кб

Скачать

☆

1 / 61 2 3 4 5 6 > Следующая >>>

ФГБОУ ВО «Воронежский государственный технический университет »

СПРАВОЧНИК МАГНИТНОГО ДИСКА

(Кафедра высшей математики и физико-математического моделирования)

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по организации самостоятельной работы по курсу «Математика» по направлениям 13.03.02 «Электроэнергетика и электротехника» (профили: «Электромеханика», «Электропривод и автоматика», «Электроснабжение», «Электропривод и автоматика робототехнических систем»), 27.03.04 «Управление в технических системах» (профиль: «Управление и информатика в технических системах»), очной формы обучения

Часть 2

Составители: А.А. Катрахова, В.С. Купцов. Е.М. Васильев

Samrab2.PDF	0,9 Mбайт 26.09.2016	уч.-изд. 3.2 л.

(название файла)	(объем файла) (дата)	(объем издания)

ФГБОУ ВО «Воронежский государственный технический университет »

(Кафедра высшей математики и физико-математического моделирования)

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Часть 2

Воронеж 2016

Составители: канд. физ.-мат. наук А.А. Катрахова, канд. физ.-мат. наук В.С. Купцов, доц. Е.М. Васильев.

УДК 517

Методические указания по организации самостоятельной работы по курсу «Математика» по направлениям 13.03.02 «Электроэнергетика и электротехника» (профили: «Электромеханика», «Электропривод и автоматика», «Электроснабжение», «Электропривод и автоматика робототехнических систем»),27.03.04 «Управление в технических системах» (профиль: «Управление и информатика в технических системах»), очной формы обучения.Ч.2/ ФГБОУ ВО «Воронежский государственный технический университет»; cост. А.А. Катрахова, В.С. Купцов, Е.М. Васильев. Воронеж, 2016. 51 с.

Методические указания содержат теоретический материал, примеры решения задач, а также задания для самостоятельной работы.

Методические указания подготовлены в эдекронном виде и содержатся вфайле «Samrab2.PDF»

Ил. 8. Библиогр.: 7 назв.

Рецензент канд. физ.-мат. наук, доц. А.П. Дубровская

Ответственный за выпуск зав. кафедрой д-р физ.-мат. наук, проф. И.Л. Батаронов

Издается по решению редакционно-издательского совета Воронежского государственного технического университета

©ФГБОУ ВО «Воронежский государственный технический университет», 2016

ВВЕДЕНИЕ

Высшая математика для будущих инженеров данного профиля является не только основой фундаментальной подготовки, но и обязательной базой для изучения остальных общетехнических специальных дисциплин и успешности всей последующей практической деятельности. И главное при этом, чтобы с самого начала и на всем протяжении курса изучение высшей математики проходило студентами целенаправленно во взаимосвязи с другими дисциплинами и ориентацией на конкретное практическое приложение изученного материала. Это возможно только при условии эффективного сочетания обязательных учебных занятий и продуктивной самостоятельной работы студентов.

При организации изучения курса высшей математики ряд тем выделяется студентам на самостоятельное изучение

ЗАНЯТИЕ № 15

ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ БИНОМОВ. ПОДСТАНОВКИ ЧЕБЫШЕВА.

ПОДСТАНОВКИ ЭЙЛЕРА

Литература: [1], c. 361-364, 369-370, [7], c. 138.

Контрольные вопросы и задания

1.Какое выражение называется дифференциальным би-

номом?

2.В каких случаях интеграл от дифференциального бинома выражается через элементарные функции (является берущимся)?

3.С помощью каких подстановок интегрируются такие дифференциальные биномы?

4.Приведите пример интеграла от дифференциального бинома, не выражающегося через элементарные функции.

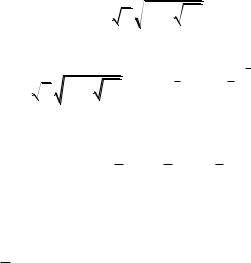
5. Какие интегралы берутся с помощью подстановок Эй-

лера?

6.Какова первая подстановка Эйлера и когда она приме-

няется?

7.Какова вторая подстановка Эйлера и когда она приме-

няется?

8.Какова третья подстановка Эйлера и когда она приме-

няется?

9.Каким еще методом берутся те же интегралы, в которых применяются подстановки Эйлера?

10.Как и какие тригонометрические подстановки используются для вычисления интегралов?

Примеры решения задач Пример 1. Найти интеграл 3x 31 3 3x2 dx .

Решение. Представим данный интеграл в следующем виде:

13x 3 1 3 3 x2 dx x3 1

2 3

3x 3 dx .

Отсюда видно, что под знаком интеграла стоит дифференци-

альный бином, при этом m 13 , n 23 , p 13 . Так как p - не целое число, то данный интеграл не относится к первому слу-

		1		1
	m 1
чаю.			3		2 - целое число, поэтому данный интеграл
	n			2

относится ко второму случаю и соответствующая подстановка:

	2																																			3
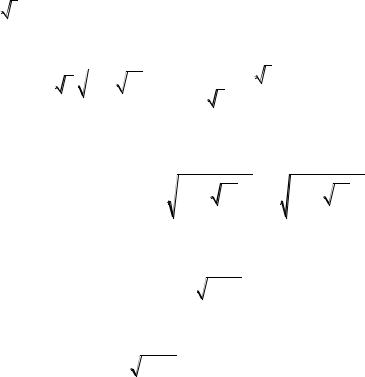
	2	t3 .																								t3 1								2


1 3x 3						Выражаем									отсюда							x																и				находим
1 3x 3						Выражаем									отсюда							x																и				находим
																												3
																												3
						1
						1
dx	3		t3 1						t2dt . Таким образом,
	3							2
	2							2
																								1
																				3				2															1

													dx t								1
				3					3 1 3 3			x2																	3			t3					1			t2dt
																																							2
							x																				t
																												2
																					3
																					3
					1											1														1				t	7			t	4
					1											1														1				t				t
										t3	1 t3dt								t6	t3				dt																		C
					2									2														2						7			4
				возвращаемся

															1		3 1 33								7						1		3 1 33										4
				к	исходной										1								x2								1										x3			C .
				к	исходной										14								x2								8										x3			C .
				переменной
Пример 2. Найти интеграл																			dx								.

																		11
																		11		1 x				4
																		x		1 x

Решение. Представим данный интеграл в следующем виде:

		dx			1
		dx
				x 11 1 x4	2 dx .
	11
	11	1 x	4
	x	1 x
Отсюда видно, что под знаком интеграла стоит диффе-
ренциальный бином, при этом				m 11, n 4 ,	p	1	. Так как
ренциальный бином, при этом				m 11, n 4 ,	p	2	. Так как
						2

p - не целое число, то данный интеграл не относится к перво-

му случаю.

m 1

11 1

- не целое число, значит дан-

ный интеграл не относится ко второму случаю.

m 1

p 3

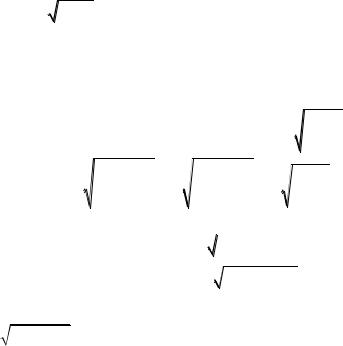
целое число, поэтому данный интеграл относится к третьему

случаю и			соответствующая										подстановка:														1 x4									x 4					1 t2 .
случаю и			соответствующая										подстановка:																x4							x 4					1 t2 .
																													x4
												x t2 1												1

Выражаем						отсюда																		4							и									находим
	1	t2	1			5
dx	1					4 t dt . Таким образом,
dx	2					4 t dt . Таким образом,
																												1
				dx					1						11									1																	5
															11																2										5

										t2 1 4																							t2				1				4 t dt
																	1
	x11								2
					1 x4
					1 x4																		t2 1
							1				2						1				t	5			2t		3
							1										1				t				2t
								t2 1				dt																	t						C
							2										2			5						3
						возвращаемся к исходной переменной
						возвращаемся к исходной переменной

																																			1				1
					с помощью обратной замены t
					с помощью обратной замены t																																	x4
																																						x4

									1 5												1 3
						1			1 5					1							1 3							1									1
							1									1																1								C .
							1		x4							1				x4												1					x4			C .
				10					x4					3						x4								2									x4
Пример 3. Найти интеграл																		dx												.

											x 1

																			x2 x 1
														R x,																				dx . В нашем
Решение. Это интеграл вида														R x,							ax2 bx c													dx . В нашем

случае a 1 0 , поэтому применим первую подстановку Эй-

лера: x2 x 1 x t . Возведя обе части равенства в квадрат,

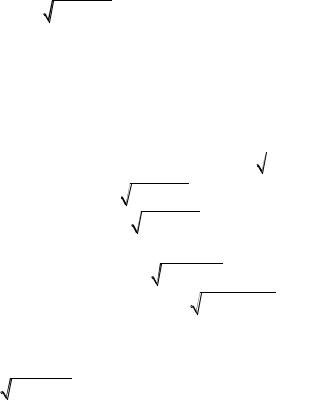
получим x2 x 1 x2 2xt t

2 . Выражаем отсюда

1 2t

находим

dx 2

t 1

. Таким образом,

2t 2

t 1 dt

x 1

1 2t 2

1 2t

2 2 dt

2 2

ln t 2 C

t 2t

t 2t 1 1

t 1

возвращаемся к исходной переменной

с помощью обратной замены t

x2 x 1 x

x 1 x 2

C .

x2 x 1 x

Пример 4. Найти интеграл

2 x x2

R x,

dx . В нашем

Решение. Это интеграл вида

ax2 bx c

случае квадратный трехчлен

2 x x2

имеет действительные

корни x1 1 и x2

2 , поэтому применим третью подстановку

x 1 t .

Эйлера:

2 x x2

Возведя обе части равенства в

квадрат, получим x 1 x 2 x 1 2 t2 . Выражаем отсюда

x		2 t2				и находим dx											6t					dt . Таким образом,
x		t2 1				и находим dx									t2			1 2				dt . Таким образом,
								dx			6														t dt						2			dt
																2 t				2		2 t			2			t2 1					2		2
					x 2 x x					2										2					2					2		t	2
					x 2 x x																					1 t						t
																	2						2			1 t
																t	2	1					2	1
																t		1			t			1
				t							возвращаемся к исходной переменной
	1		ln	t				2	C
			ln						C
2				t			2						с помощью обратной замены

																			2 x x2
																			2 x x2
												1															2
														ln						x 1							2		C .
																				x 1

												2							2 x x2


																											2
																				x 1							2
																				x 1

Задачи и упражнения для самостоятельного решения Решить задачи: [3], 2076, 2078, 2080;

Форма отчетности: устный опрос, типовой расчет, контрольная работа.

ЗАНЯТИЯ № 16

НЕСОБСТВЕННЫЕ МНТЕГРАЛЫ.

ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

Литература: [1], c. 429-448, [7], c. 141-146.

Контрольные вопросы и задания

1.Как вычисляются несобственные интегралы 1 рода ( с бесконечными пределами ) ?

2.Сформулируйте признаки сходимости несобственныхинтегралов 1 рода ?

3.Как вычисляются несобственные интегралы 2 рода ( от неограниченной функции ) ?

4.Сформулируйте признаки сходимости несобственныхинтегралов 2 рода.

5. Как вычислить с помощью определенного интеграла площадь плоской фигуры в случае задания ее границы в явном виде, в полярных координатах, параметрическими уравнениями?

6. Вычислите с помощью определенного интеграла длину дуги кривой в случае задания ее уравнением в явном виде, параметрическом виде, в полярных координатах?

7. Как вычислить объем тела по площадям поперечных сечений; объем тела вращения вокруг оси Ox , оси Oy ?

8. Как вычислить поверхность тела вращения?

9. Как найти величину работы с помощью определенного интеграла?

10. Найдите координаты центра тяжести плоской линии, плоской фигуры?

Примеры решения задач

			dx
Пример 1.Вычислить 2				.
Пример 1.Вычислить 2	x	2	x 2	.
	x		x 2

Решение. Это несобственный интеграл с бесконечным верхним пределом. Так как подынтегральная дробь разлагается на простейшие дроби вида

						1				1			1						1			то
																					, то
	x	2		x 2						3							x		2		, то
	x			x 2						3	x 1						x		2
						dx									b				dx							1	b			1	1
2										lim 2													lim				2					dx
2			x		2	x			2	lim 2						x		2	x				lim			3	2					dx
			x			x			2		b					x			x	2				b		3		x 1			x 2
lim							1	ln	x 1			b		1	lim \| ln							b 1		ln	1		\|	2	ln 2.
							1		x 1			b		1								b 1			1			2
									x 2													b 2
		b					3					2		3		b									4		3
		b					3					2		3		b									4		3
																												7

1 / 61 2 3 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.2022288.61 Кб3Учебное пособие 124.pdf
#
30.04.2022898.88 Кб26Учебное пособие 1240.pdf
#
30.04.2022899.42 Кб11Учебное пособие 1241.pdf
#
30.04.2022900.68 Кб3Учебное пособие 1242.pdf
#
30.04.2022902.67 Кб55Учебное пособие 1243.pdf
#
30.04.2022902.72 Кб2Учебное пособие 1244.pdf
#
30.04.2022905.24 Кб6Учебное пособие 1245.pdf
#
30.04.2022906.77 Кб7Учебное пособие 1246.pdf
#
30.04.2022907.47 Кб2Учебное пособие 1247.pdf
#
30.04.2022907.69 Кб4Учебное пособие 1248.pdf
#
30.04.2022908.02 Кб4Учебное пособие 1249.pdf