
Теоретическая механика. методические указания к выполнению лабораторных работ. Переславцева Н.С., Воропаев А.А
.pdfМИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Воронежский государственный технический университет»
Кафедра прикладной математики и механики
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ к выполнению лабораторных работ
для студентов специальности 24.05.07 «Самолето- и вертолетостроение»
испециальности 24.05.02 «Проектирование авиационных
иракетных двигателей»
очной формы обучения
Воронеж 2022
УДК 531(07) ББК 22.21я7
Составители:
канд. физ.-мат. наук Н. С. Переславцева, канд. техн. наук А. А. Воропаев,
д-р техн. наук Д. В. Хван, канд. техн. наук Л. В. Хливненко, канд. техн. наук О. А. Семенихин
Теоретическая механика: методические указания к выполнению лабораторных работ / ФГБОУ ВО «Воронежский государственный технический университет»; сост.: Н. С. Переславцева, А. А. Воропаев, Д. В. Хван, Л. В. Хливненко, О. А. Семенихин. Воронеж: Изд-во ВГТУ, 2022. 34 с.
Методические указания проведения лабораторных работ включают правила оформления и содержание заданий лабораторных работ № 1–4.
Предназначены для студентов специальности 24.05.07 «Самолето- и вертолетостроение» и специальности 24.05.02 «Проектирование авиационных и ракетных двигателей» 1–2 курсов очной формы обучения.
Методические указания подготовлены в электронном виде и содержатся в файле ТМ ЛР СВС+РД.pdf.
Ил. 10. Табл. 3. Библиогр.: 7 назв.
УДК 531(07) ББК 22.21я7
Рецензент – А. В. Келлер, д-р. физ.-мат. наук, доц. кафедры прикладной математики и механики ВГТУ
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
2
ЛАБОРАТОРНАЯ РАБОТА № 1
Определение кинематических характеристик при сложном движении точки
Цель работы: научиться определять кинематические характеристики движения точки с помощью теорем сложения скоростей и ускорений.
Порядок выполнения работы:
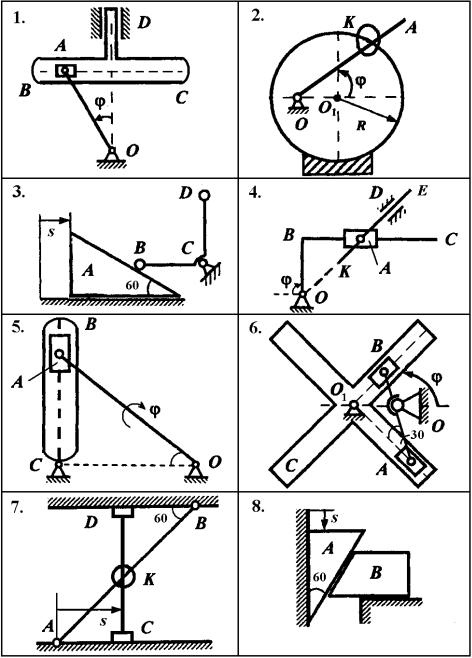
1.Схемы механизмов приведены на рис. ЛР1.1–ЛР1.3, дополнительные условия – в табл. ЛР1.
2.Построить схему механизма в соответствии с положением, которое он занимает в заданный момент времени.
3.Определить, какое движение для точки является абсолютным, переносным, относительным. Соотнести заданный по условию закон движения
(t) , s s(t) или x x(t) с одним из этих движений
4.Определить, как должны быть направлены абсолютная, переносная и относительная скорости точки. Вычислить и изобразить на чертеже скорость движения, заданного по условию, для заданного момента времени t1 .
5.Используя теорему сложения скоростей
v ve vr ,
провести геометрическое разложение вычисленной скорости на составляющие. Аналитически вычислить их значение.
6. Аналогично п. 4–5 вычислить, изобразить на чертеже ускорение движения, заданного по условию, в момент времени t1 . Используя теорему сложения ускорений
a ae ar aК ,
провести геометрическое разложение вычисленной скорости на составляющие. Аналитически вычислить их значение.
Варианты:
1) В кривошипно-кулисном механизме кривошип ОА ( ОА R ) вращается вокруг неподвижной опоры O по закону (t) ( – в радианах, t – в секундах). Кулисный камень A , перемещаясь по вертикальной кулисе BC , приводит её в движение вдоль оси симметрии в горизонтальных направляющих D . Определить скорость и ускорение кулисы BC в момент времени t1 .
2) Кольцо K , соединяет неподвижное кольцо радиусом R и подвижный стержень AО , вращающийся вокруг неподвижной опоры O по закону(t) ( – в радианах, t – в секундах). OO1 0,75R . Определить абсолютные и относительные скорость и ускорение точки K в момент времени t1 .
3
3) Клин А движется по горизонтальной поверхности по закону s s(t) ( s – в сантиметрах, t – в секундах). На клин опирается ломаный стержень BCD , вращающийся вокруг неподвижной опоры С (плечо ВС R и горизонтально). Определить угловую скорость и угловое ускорение стержня BCD в момент вре-
мени t1 .
4) В кривошипно-рычажном механизме ломаный стержень OBC вращается вокруг неподвижной опоры O по закону (t) ( – в радианах, t – в секундах). При этом ползун A приводит в движение стержень КЕ , который перемещается в наклонных направляющих D . OВ BA R . Определить скорость и ускорение стержня КЕ в момент времени t1 .
5) В кривошипно-кулисном механизме кривошип ОА ( OA R) вращается вокруг неподвижной опоры O по закону (t) ( – в радианах, t – в секундах). Кулисный камень A , перемещаясь по кулисе BC , приводит её в движение.. Определить угловую скорость и угловое ускорение кулисы BC в момент времени t1 .
6)Коромысло AB вращается вокруг неподвижной опоры O по закону
(t) ( – в радианах, t – в секундах), приводя во вращение вокруг оси O1
прямоугольную крестовину С . Ползуны |
A и B скользят вдоль взаимно пер- |
||
пендикулярных прорезей крестовины С . |
OO1 AO OB R . Определить угло- |
||
вую скорость и угловое ускорение крестовины С в момент времени t1 . |
|||
7) |
Кольцо K соединяет неподвижный стержень AB |
и стержень CD |
|
( CD R ), движущийся поступательно по закону s АС s(t) ( s |
– в сантиметрах, |
||
t – в секундах). Определить абсолютные и относительные скорость и ускорение кольца K , скользящего по стержням, в момент времени t1 .
8)Клин А движется по вертикальной поверхности по закону s s(t) ( s
–в сантиметрах, t – в секундах). Он приводит призму B в движение по горизонтальной поверхности. Определить скорость и ускорение призмы B в момент времени t1 .
9)В кривошипно-кулисном механизме кулиса BC вращается непо-
движной опоры |
С по закону (t) ( – в радианах, t – в секундах). Кулис- |
ный камень A , |
перемещаясь по кулисе BC , приводит в движение ломаный |
стержень АKE ( АK R ), который перемещается в горизонтальных направляющих D . Определить скорость и ускорение стержня CKE в момент времени t1 .
10) В кривошипно-рычажном механизме кривошип ОА ( OA R) вращается вокруг неподвижной опоры O по закону (t) ( – в радианах, t – в секундах). При этом ползун A приводит в движение ломаный стержень BCК , который перемещается в вертикальных направляющих D . Определить скорость и ускорение стержня BCК в момент времени t1 .
11) |
Крестообразный ползун K соединяет неподвижный вертикальный |
стержень |
AB и горизонтальный стержень CD . Ползун D движется поступа- |
|
4 |
тельно в направляющих по закону s AD s(t) ( s – в сантиметрах, t – в секундах). AB 2R . Определить абсолютные и относительные скорость и ускорение
ползуна K , скользящего по стержням, в момент времени t1 . |
|
|
|
|
12) Кольцо |
K , соединяющее неподвижное кольцо радиусом R и по- |
|||
|
|
|
|
|
движный стержень |
AО , движется вдоль окружности по закону |
s OK s(t) |
( s |
– |
в сантиметрах, t – в секундах). Определить абсолютные и относительные скорость и ускорение кольца K в момент времени t1 .
13) В кривошипнокулисном механизме кривошип ОА ( OA R) вращается вокруг неподвижной опоры O по закону (t) ( – в радианах, t – в секундах). Кулисный камень A , перемещаясь по наклонной кулисе BC , приводит её в движение вдоль оси симметрии в горизонтальных направляющих D . Определить скорость и ускорение кулисы BC в момент времени t1 .
14)Коромысло AB вращается вокруг неподвижной опоры O по закону
(t) ( – в радианах, t – в секундах), приводя во вращение вокруг оси O1
прямоугольную крестовину С . Ползуны A и B скользят вдоль взаимно перпендикулярных прорезей крестовины С . OO1 AO OB R . Определить угловую скорость и угловое ускорение крестовины С в момент времени t1 .
15) Клин А движется по горизонтальной поверхности по закону s s(t) ( s – в сантиметрах, t – в секундах). На клин опирается стержень BC , движущийся в вертикальных направляющих D . Определить скорость и ускорение стержня BC в момент времени t1 .
16) Круговой кулачок А радиусом R движется поступательно по закону s s(t) ( s – в сантиметрах, t – в секундах), приводя в движение из наивысшего положения стержень BС в вертикальных направляющих D . Определить скорость и ускорение стержня BС в момент времени t1 , когда он опустится на высоту h 12 см.
17) В кривошипно-кулисном механизме кривошип ОА ( OA 3R) вращается вокруг неподвижной опоры O по закону (t) ( – в радианах, t – в секундах). Кулисный камень A , перемещаясь по наклонной кулисе BC ( ОC 4R) , приводит её в движение. Определить угловую скорость и угловое ускорение кулисы BC в момент времени t1 .
18)Кольцо K , соединяющее неподвижное полукольцо радиусом R и
подвижный |
стержень |
ВС , движется вдоль |
полуокружности |
по |
закону |
||
|
|
|
|
|
|
|
|
s AK s(t) |
( s – в сантиметрах, |
t – в секундах). Определить абсолютные и от- |
|||||
носительные скорость и ускорение кольца K в момент времени t1 . |
|
|
|||||
19) |
В стержневом механизме крестообразный ползун K соединяет не- |
||||||
подвижный стержень |
AB |
и перпендикулярный ему стержень CD . Ползун D |
|||||
движется |
поступательно |
в |
горизонтальных |
направляющих |
по |
закону |
|
s AD s(t) |
( s – в сантиметрах, |
t – в секундах). Определить абсолютные и от- |
|||||
|
|
|
|
5 |
|
|
|
носительные скорость и ускорение ползуна K , скользящего по стержням, в момент времени t1 .
20) Маховик А радиусом R вращается вокруг неподвижной опоры O по закону (t) ( – в радианах, t – в секундах), приводя в движение стержень BС в вертикальных направляющих D .. OO1 0,5R . Определить скорость и ускорение стержня BС в момент времени t1 .
21) В кривошипно-кулисном механизме стержень AK движется в горизонтальных направляющих D по закону x x(t) ( x – в сантиметрах, t – в секундах). Кулисный камень A , перемещаясь по кулисе BC , приводит её в движение. Определить угловую скорость и угловое ускорение кулисы BC в момент времени t1 .
22) В стержневом механизме крестообразный ползун K соединяет неподвижный горизонтальный стержень AB и вертикальный стержень CD , движущийся по закону ( s – в сантиметрах, t – в секундах). AB 2R . Определить абсолютные и относительные скорость и ускорение ползуна K , скользящего по стержням, в момент времени t1 .
23)Кольцо K соединяет неподвижный стержень BC и полукольцо ра-
диусом R , движущееся поступательно по закону s s(t) ( s – в сантиметрах, t – в секундах). Определить абсолютные и относительные скорость и ускорение кольца K в момент времени t1 .
24) Призма B движется по горизонтальной поверхности по закону s s(t) ( s – в сантиметрах, t – в секундах). На призму опирается клин А , движущийся в вертикальных направляющих. Определить скорость и ускорение клина А в момент времени t1 .
25) В кривошипно-рычажном механизме кривошип ОА ( OA R) вращается вокруг неподвижной опоры O по закону (t) ( – в радианах, t – в секундах). При этом ползун A приводит в движение ломаный стержень BCК , который перемещается в горизонтальных направляющих D . Определить скорость и ускорение стержня BCК в момент времени t1 .
|
|
|
|
|
Таблица ЛР1 |
|
|
|
|
|
|
|
|
№ варианта |
(t) , |
s s(t) , |
x x(t) , |
R , |
t1 , |
|
рад |
см |
см |
см |
с |
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
|
|
|
1. |
t 2 |
|
|
20 |
1 |
|
6 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
0,25 t 2 |
|
|
100 |
1 |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
Продолжение таблицы ЛР1
3. |
|
|
|
|
|
|
t |
|
|
|
40 |
2 |
|
|
|
|
|
10sin |
|
|
|
||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
4. |
4sin t |
|
|
|
|
|
|
20 |
0,75 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
|
t |
|
|
|
|
|
|
|
40 |
2 |
|
|
sin |
|
|
|
|
|
|
|
||||
|
3 |
12 |
|
|
|
|
|
|
|
|
||
6. |
|
t |
|
|
|
|
|
|
|
40 |
2 |
|
2sin |
|
|
|
|
|
|
|
|
||||
|
|
6 |
|
|
|
|
|
|
|
|
|
|
7. |
|
|
|
|
|
|
t |
|
|
|
50 |
5 |
|
|
|
|
|
10sin |
|
|
|
||||
|
|
|
|
|
|
|
6 |
|
|
|
|
|
8. |
|
|
|
|
|
|
10t 2 |
|
|
|
|
1 |
9. |
|
t |
|
|
|
|
|
|
|
40 |
2 |
|
|
sin |
|
|
|
|
|
|
|
||||
|
2 |
4 |
|
|
|
|
|
|
|
|
|
|
10. |
|
t |
|
|
|
|
|
|
|
|
20 |
2 |
|
8 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11. |
|
|
|
|
|
|
|
|
t |
|
|
1 |
|
|
|
|
|
|
|
|
40sin |
|
|
||
|
|
|
|
|
|
|
|
|
6 |
|
|
|
12. |
|
|
|
|
|
|
2 t 2 |
|
|
|
48 |
2 |
|
|
|
t 2 |
|
|
|
|
|
|
|
|
|
13. |
|
sin |
|
|
|
|
|
|
|
|
60 |
2 |
6 |
|
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
14. |
|
t |
|
|
|
|
|
|
|
20 |
1 |
|
|
sin |
|
|
|
|
|
|
|
||||
|
2 |
6 |
|
|
|
|
|
|
|
|
|
|
15. |
|
|
|
|
|
|
t |
|
|
|
|
2 |
|
|
|
|
|
50sin |
|
|
|
|
|||
|
|
|
|
|
|
|
6 |
|
|
|
|
|
16. |
|
|
|
|
|
|
t |
|
|
|
30 |
2 |
|
|
|
|
|
48sin |
|
|
|
||||
|
|
|
|
|
|
|
12 |
|
|
|
|
|
17. |
|
t |
|
|
|
|
|
|
|
20 |
2 |
|
sin |
|
|
|
|
|
|
|
|
||||
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
t |
|
|
|
|
||
18. |
|
|
|
|
|
|
sin |
|
|
|
10 |
2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
3 |
12 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
19. |
|
|
|
|
|
|
|
|
t |
|
|
2 |
|
|
|
|
|
|
|
|
40sin |
|
|
||
|
|
|
|
|
|
|
|
|
12 |
|
|
|
20. |
|
t / 4 |
|
|
|
|
|
|
|
40 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21. |
|
|
|
|
|
|
|
|
t |
|
|
2 |
|
|
|
|
|
|
|
|
50sin |
|
|
||
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
Окончание таблицы ЛР1
22. |
|
|
|
10t 2 |
|
|
2 |
23. |
|
|
|
20sin( t / 6) |
|
40 |
1 |
|
|
|
|
|
|
|
|
24. |
|
|
|
14t t 2 |
|
|
2 |
25. |
|
t |
|
|
|
4 |
2 |
|
|
sin |
|
|
|
|
|
|
4 |
12 |
|
|
|
|
|
Рис. ЛР1.1.
8
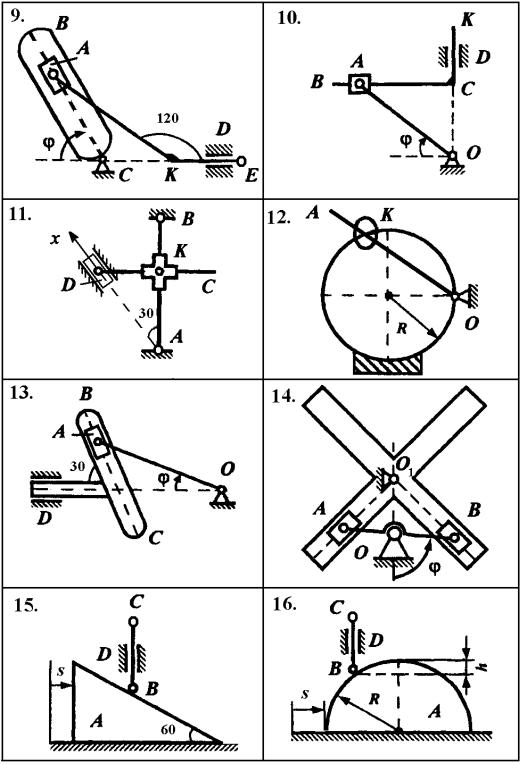
Рис. ЛР1.2.
9
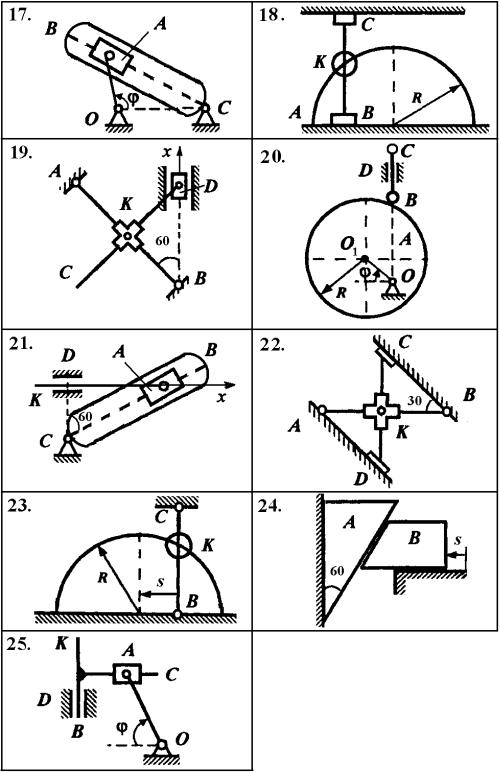
Рис. ЛР1.3
10
