
Учебное пособие 1029
.pdfФГБОУ ВПО «Воронежский государственный технический университет»
Кафедра систем информационной безопасности
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к практическим занятиям по дисциплине «Математические основы риск-анализа» для студентов специальностей
090301 «Компьютерная безопасность»,
090302 «Информационная безопасность телекоммуникационных систем», 090303 «Информационная безопасность автоматизированных систем»
очной формы обучения
Воронеж 2014
Составители: д-р техн. наук А.Г. Остапенко, асп. М.В. Бурса
УДК 681.3
Методические указания к практическим занятиям по дисциплине «Математические основы риск-анализа» для студентов специальностей 090301 «Компьютерная безопасность», 090302 «Информационная безопасность телекоммуникационных систем», 090303 «Информационная безопасность автоматизированных систем» очной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; сост. А.Г. Остапенко, М.В. Бурса. Воронеж, 2014. 44 с.
Методические указания посвящены вопросам анализа параметров риска для различных вероятностях реализации атак на системы.
Методические указания подготовлены в электронном виде в текстовом редакторе и содержатся в файле Бурса_ПЗ_MOРA.pdf.
Табл. 9. Ил. 2. Библиогр.: 15 назв.
Рецензент д-р техн. наук, проф. О.Н. Чопоров
Ответственный за выпуск зав. кафедрой, д-р техн. наук, проф. А.Г. Остапенко
Издается по решению редакционно-издательского совета Воронежского государственного технического университета.
© ФГБОУ ВПО «Воронежский государственный технический университет», 2014
МЕРЫ РИСКА СИСТЕМ НА ОСНОВЕ ВЕРОЯТНОСТНЫХ ПАРАМЕТРОВ
ИХАРАКТЕРИСТИК УЩЕРБА
1.Аналитический подход к расчету параметров рисков
для компонентов систем
Реализация атак на систему может нанести ей ущерб некоторой величины. Атаки на компоненты систем являются многоплановыми и непредсказуемыми и, зачастую, не оставляют надежд для детерминированного описания этих процессов и возникающих в результате их реализации ущербов. В связи с этим можно полагать, что ущерб от атак данного типа является случайной величиной. Для описания ущерба как случайной величины используется аппарат теории вероятностей и математической статистики, практикующий подход с использованием различных функций и законов распределения вероятности случайной величины, среди которых наибольшей популярностью пользуются регулярные законы. В этом классе наиболее практическое применение нашли законы, определенные на [0;+ ): экспоненциальный и логнормальный законы; гамма-распределение; распределение Эрланга, Вейбула и Релея [1].
Функция распределения является основой для исследования непрерывных случайных величин. Непрерывная случайная величина – случайная величина, значения которой образуют несчетные множества. Значение функции распределения непрерывной случайной величины в точке определяет вероятность того, что случайная величина примет значение, меньше заданного.
Плотность или закон распределения вероятностей случайной величины имеет смысл первой производной функции распределения. Соответственно интегральная функция распределения плотности вероятности имеет вид [2]:
1
|
|
(x) (x)dx. |
(1.1) |
Так как ущерб – величина положительная, то интегральная функция распределения представляет собой определенный интеграл от плотности распределения в пределах от 0 до + .
(u) (u)du.
0
(1.2)
Основными характеристиками ущерба как случайной величины являются:
-математическое ожидание (имеет смысл среднего значения ущерба, начальный момент первого порядка);
-дисперсия (характеризует разброс значений ущерба относительно математического ожидания, центральный момент второго порядка);
-центральные моменты третьего и четвертого порядков (определяются математическим ожиданием разности между текущим значением и начальным моментом первого порядка, возведенной в соответствующую степень).
Важнейшей характеристикой при оценке ущерба является математическое ожидание, характеризующее его среднее значение. Формула для расчета математического ожидания имеет следующий вид:
u |
|
|
|
M [U ] |
|
u (u)du, |
|
m |
|
||
|
|
0 |
|
(1.3)
для непрерывного распределения вероятностей ущерба. Дисперсия также является весьма важной характеристикой ущерба как случайной величины. Дисперсия показывает разброс случайной величины относительно ее математического ожидания. Дисперсия ущерба определяется по формуле
(1.4):
D[U] M[(U m )2 |
]. |
(1.4) |
u |
|
|
2

Среднеквадратическое отклонение
ный момент) ущерба имеет вид |
|
D[U ] |
|
|
(первый централь-
.
Следует также отметить, что крайне важное значение имеют начальные и центральные моменты.
Начальным моментом k-го порядка случайно распределенной величины ущерба в общем виде является математическое ожидание k-й степени его величины.
|
|
k |
], |
[U ] M[U |
|||
k |
|
|
|
|
|
|
|
k |
k |
(u)du. |
|
u |
|||
|
0 |
|
|
(1.5)
(1.6)
Центральным моментом порядка k случайной величины ущерба называется математическое ожидание k-й степени соответствующей центрированной случайной величины [3]:
|
k |
], |
[U ] M[(U m ) |
||
k |
u |
|
k (u M )k (u)du.
0
(1.7)
(1.8)
Следует отметить, что первый начальный момент – нечто иное как математическое ожидание ( mx 1 ), а второй цен-
тральный момент – это дисперсия случайной величины ущерба
( D[U ] 2 ).
С использованием этих величин вводится коэффициент асимметрии распределения значений ущерба в системе:
A |
[U ] |
. |
|
3 |
|
||
|
|
|
|
s |
|
3 |
|
|
u |
|
|
|
|
|
|
(1.9)
Коэффициент асимметрии показывает, насколько распределен ущерб относительно своего среднего значения, и не имеется ли в распределении асимметрии. Используя коэффициент асимметрии, можно узнать о направленности асимметрии. Если As>0, то распределение имеет правостороннюю асимметрию, а если As<0 – асимметрия левосторонняя.
3

Четвертый центральный момент является характеристикой островершинности распределения ущерба. Для того, чтобы описать это свойство, в теории вероятностей с помощью него вводится эксцесс случайной величины.
|
|
|
|
[U ] |
3. |
||
E |
|
4 |
|
|
|||
x |
|
4 |
|||||
|
|
|
|||||
|
|
|
u |
|
|||
|
|
|
|
|
|
||
(1.10)
Коэффициент эксцесса ущерба показывает, является ли распределение ущерба более островершинными, нежели нор-
мальное (нормальное распределение имеет
E |
u |
|
0
). При зна-
чении |
( Eu 0 ) распределение более островершинно, а при |
Eu 0 |
- менее. |
|
Мода – значение случайной величины, имеющее |
наибольшую вероятность. |
|
|
U0 – мода, соответствующая максимальному значению |
(u) . |
|
|
Риск может быть найден как произведение величины |
ущерба на вероятность наступления данного ущерба [4, 5, 6, 7, 8].
Risk
U |
t |
|
P(U |
) |
t |
|
,
(1.11)
где Ut - ущерб от реализации атак,
P(Ut) - вероятность наступления ущерба U.
Для нахождения риска системы в целом, необходимо определить аналитические параметры риска.
Начальные моменты риска определяются следующим образом:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
uk Risk(u)du |
|
uk u (u)du |
|
uk 1 (u)du |
k 1 . (1.12) |
|||||
k |
|
0 |
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Risk(u)du |
|
|
u (u)du |
|
|
u |
(u)du |
k |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
0 |
|
|
0 |
|
|
0 |
|
|
|
4

Отсюда среднее значение
равно:
M
ущерба для кривой риска
|
2 |
. |
(1.13) |
|
|||
|
|
||
|
|
||
1 |
|
|
|
|
|
|
Центральный момент риска k-го порядка находится следующим образом:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(u M ) |
k |
Risk(u)du |
|
|
(u M ) |
k |
u (u)du |
|
|
(u M ) |
k |
u (u)du |
|
|
|
|
|
|
|
|
|
. |
|||||||||
|
0 |
|
|
|
0 |
|
|
|
0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Risk(u)du |
|
|
u (u)du |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
(1.14)
Найдем центральные моменты 2-го, 3-го и 4-го поряд-
ка.
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
u (u)du |
|
(u |
2 |
|
2uM M |
2 |
)u (u)du |
||||||||||
|
(u M ) |
|
|
|
|
|||||||||||||||||
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
(u |
3 |
2u |
M |
uM |
2 |
) (u)du |
|
( 3 |
2 2 M |
1M |
2 |
) |
||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3 2 2 M M 2 .1 1
Отсюда среднеквадратическое отклонение будет равно:
|
|
α3 |
2M* |
α2 |
M* 2 . |
|
α1 |
α1 |
|||||
|
|
|
|
Но, так как:
1 u (u)du M ,
0
5
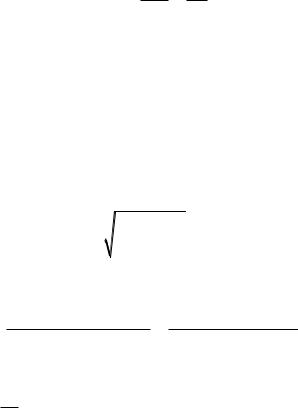
то
|
|
M |
|
1 1 |
|
|
|
||||
1 |
|
|
|||
|
|
|
|||
|
|
|
1 |
||
|
|
|
|
|
|
2 1
.
Следовательно, центральный момент 2-го порядка может быть выражен следующим образом:
|
|
|
|
3 |
( |
|
2 |
) |
, |
|
|
|
|
|
|
2 |
|
||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
1 |
|
|
||
и среднеквадратическое отклонение:
|
|
|
|
|
3 |
( 2 )2 . |
|
|
|
|
|
|
1 |
1 |
|
(1.15)
(1.16)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
u (u)du |
|
|
|
|
|
|
|
|
(u M ) |
Risk(u)du |
|
(u M ) |
|||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Risk(u)du |
|
|
|
u (u)du |
|||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(u |
3 |
|
|
2 |
M 3M |
2 |
u |
M |
3 |
)u (u)du |
|||||
|
|
|
|
|
|
|
3u |
|
|
||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( u4 (u)du 3M u3 (u)du 3M 2 |
u2 (u)du M 3 u (u)du) |
|||||||||||||||||||||
1 |
|||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
0 |
||
|
1 |
( |
|
3 |
M 3M 2 |
|
M 3 ) 4 |
3M 3 3M 2 2 M 3. |
|||||||||||||||
|
4 |
2 |
|||||||||||||||||||||
|
1 |
|
3 |
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
1 |
|
1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
6

Осуществляя соответствующие подстановки, имеем:
|
|
|
|
|
3 |
|
|
3 |
|
3 |
( |
|
|
) |
|
|
|
|
3 |
|
|
2 |
|
3 |
, |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
4 |
2 |
|
3 |
|
2 |
|
2 |
3 |
|
4 |
2 |
|
3 |
|
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
3 |
|
|
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
2 |
|
|
3 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
|
1 |
|
|
1 |
|
|
1 |
|
|
|
|
1 |
|
1 |
|
|
1 |
|
||||
(1.17)
|
|
|
|
|
|
|
|
|
|
|
|
(u M ) |
4 |
|
|
4 |
u (u)du |
|
|
|
|
Risk (u)du |
|
(u M ) |
||
|
0 |
|
|
0 |
|
|||
|
|
|
|
|
|
|
||
|
4 |
|
|
|
|
|
|
|
|
|
|
Risk (u)du |
|
u (u)du |
|||
|
|
|
0 |
|
|
|
0 |
|
(u4 4u3M 6M 2u2 4M 3u M 4 )u (u)
4 0
5 4M 4 6M 2 3 4M 3 2 M 4 .1 1 1 1
Осуществляя соответствующие подстановки, имеем:
|
|
|
|
|
4 |
|
|
6 |
|
2 |
4 |
|
4 |
|
|
4 |
|
|
|
4 |
|
|
6 |
|
2 |
3 |
|
4 |
. |
||||||
|
|
5 |
4 |
|
2 |
3 |
|
|
2 |
|
2 |
|
2 |
|
5 |
4 |
|
2 |
3 |
|
|
2 |
|
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
4 |
|
|
|
|
2 |
|
|
|
3 |
|
|
4 |
|
4 |
|
|
|
|
2 |
|
|
|
3 |
|
|
4 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
1 |
|
1 |
|
|
|
1 |
|
|
1 |
|
1 |
|
|
1 |
|
1 |
|
|
|
1 |
|
|
|
1 |
|
||||||
(1.18)
Приведем соотношения, связывающие центральные и начальные моменты различных порядков. Особенность состоит в том, что эти соотношения справедливы как для дискретных, так и для непрерывных случайных величин.
1 0, |
|
|
|
|
|
|
|
|||
|
|
|
2 |
2 |
, |
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
||
|
|
|
3 |
3 1 |
3 |
, |
|
|
|
|
3 |
|
2 2 1 |
|
|
|
|||||
|
|
|
4 |
|
|
|
2 |
|
4 |
|
4 |
|
4 |
3 1 6 2 1 |
3 1 |
, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7
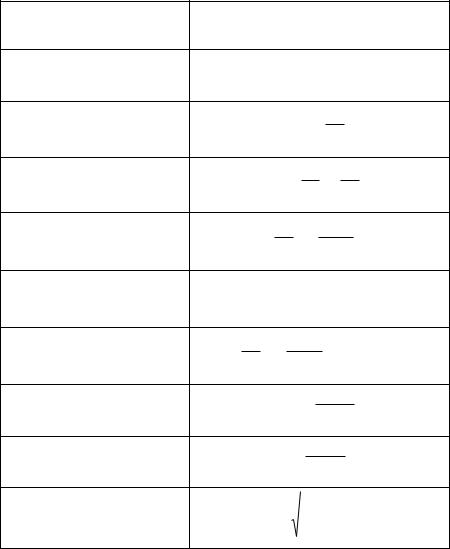
Для удобства дальнейшего анализа все аналитические выражения для расчета параметров риска сведены в табл. 1.
Таблица 1
Обобщенные аналитические выражения для расчета параметров риска
Параметры риска
k-й начальный момент
Математическое ожидание (1-й начальный момент)
2-й центральный момент (дисперсия)
3-й центральный момент
4-й центральный момент
4-й центральный момент
Коэффициент асимметрии
Коэффициент эксцесса
Среднеквадратическое
отклонение
Аналитические выражения параметров
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
( |
|
2 |
) |
2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
2 |
|
3 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
2 |
|
|
3 |
|
|
2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
4 |
||||||||||
|
|
|
|
|
4 |
|
|
4 2 |
|
|
6 |
|
|
3 |
|
|
|
2 3 |
|
2 |
||||||||||||||
4 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
4 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
4 |
|
|
|
|
|
6 |
|
2 |
3 |
|
4 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
5 |
|
|
4 |
|
|
2 |
|
|
|
3 |
|
|
|
2 |
|
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
4 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
4 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
A |
|
|
[U ] |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
E |
|
|
|
|
4 |
[U ] |
|
3 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
( 2 )2 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||
8
