Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

Высшая математика

Файл:

Кратные интегралы. Методические указания для организации самостоятельной работы по курсу Высшая математика. Пантелеев И.Н

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

622 Кб

Скачать

☆

1 / 61 2 3 4 5 6 > Следующая >>>

ГОУВПО «Воронежский государственный технический университет»

Кафедра высшей математики и физико-математического моделирования

КРАТНЫЕ ИНТЕГРАЛЫ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ для организации самостоятельной работы

по курсу "Высшая математика" для студентов специальностей 280103 "Защитавчрезвычайныхситуациях", 280101 "Безопасностьжизнедеятельности"

и направления 280200 "Защитаокружающейсреды" очной формы обучения

Воронеж 2010

Составитель канд. физ.-мат. наук И.Н. Пантелеев

УДК 51 (075)

Кратные интегралы: Методические указания для организации самостоятельной работы по курсу "Высшая математика" для студентов специальностей 280103 "Защита в чрезвычайных ситуациях", 280101 "Безопасность жизнедеятельности" и направления 280200 "Защита окружающей среды" очной формы обучения / Воронеж. гос. техн. ун-т; Сост. И.Н. Пантелеев. Воронеж, 2010. 53 с.

Настоящие методические указания предназначены в качестве руководства для организации самостоятельной работы

по курсу "Высшая математика" по разделу «Кратные интегралы» для студентов специальности 280103 (ЧС) и 280101 (БЖ) в 3 семестре. В работе приведен теоретический материал, необходимый для выполнения заданий и решение типовых примеров.

Методические указания подготовлены на магнитном носителе в текстовом редакторе Microsoft Word 2003 и

содержатся в файле Vmfmm_KratInt1.pdf.

Ил. 31. Библиогр.: 8 назв.

Рецензент канд. физ.-мат. наук, доц. В.В. Ломакин Ответственный за выпуск зав. кафедрой д-р физ.-мат. наук, проф. И.Л. Батаронов

Издается по решению редакционно-издательского совета Воронежского государственного технического университета

1. Двойной интеграл и его вычисление

1°. Двойной интеграл является обобщением понятия опре-

деленного интеграла на случай функции двух переменных f(x, у) и представляет конечный предел двумерной интегральной суммы в области (S).

∫∫ f (x, y)maxlimx →0∑∑ f (xi , y j ) xi yj .					(1)
(S )		i	i	j
	max	yi →0
где xi y j = (xi+1 − xi )(y j+1 − y j )				- площади элементарных об-

ластей, на которые разбивается плоская область S.

На двойной интеграл распространяются свойства простого определенного интеграла: постоянный множитель можно выносить за знак интеграла, интеграл от суммы функций равен сумме интегралов от этих функций, область интегрирования можно разбивать на части.

2°. Вычисление двойного интеграла сводится к последовательному вычислению двух обыкновенных определенных интегралов

b	y2	(x)	f (x, y)dy
∫dx	∫		f (x, y)dy	(2)
a y1		(x)
или		(y)
c	x2	(y)	f (x, y)dx
∫dy	∫		f (x, y)dx	(3)
d	x1 (y)

Если внутренний интеграл берется по переменной у, то переменная х рассматривается как постоянная, а если по х, то постоянной будет у. Пределы интегрирования во внутреннем интеграле как правило являются переменными и зависят от переменной, которая рассматривается как постоянная, пределы же внешнего интеграла всегда постоянны. Пределы интегрирования внутреннего и внешнего интеграла постоянны только тогда, когда область интегрирования является прямоугольником со сторонами, параллельными осям координат.

Область интегрирования интеграла (2) (рис. 1) a ≤ x ≤ b , y1 (x)≤ y ≤ y2 (x) такова, что любая прямая, параллельная оси у, пересекает ее границу только два раза. Вычисление двойного интеграла по области d ≤ y ≤ c , x1 (y)≤ x ≤ x2 (y)

(рис. 2) целесообразно выполнять по формуле (3), поскольку любая прямая, параллельная оси х, пересекает границу области только два раза.

Рис. 1

Рис. 2

3°. Если верхняя или нижняя граница области описывается несколькими функциями (рис. 3), то область интегрирования следует разбить прямой х = с на две области S1 и S2. Двойной интеграл по области S в этом случае разбивается на сумму интегралов

∫∫ f (x, y)dxdy = ∫∫ f (x, y)dxdy +∫∫				f (x, y)dxdy =
(S )	(S1 )		(S2 )	(4)
= ∫c	y(x)	(x, y)dy + ∫b	y(x)
	dx ∫ f		dx ∫ f (x, y)dy.
a	y1 (x)	c	y2 (x)

Рис. 3 Если левая или правая граница области описывается не-

сколькими функциями (рис. 4), то область интегрирования S разбивается на две области S1 и S2, а двойной интеграл вычисляется по формуле

∫∫ f (x, y)dxdy = ∫∫ f (x, y)dxdy +∫∫				f (x, y)dxdy =
(S )		(S1 )	(S2 )	(5)
= ∫b	x(y)		x(y)	(5)
= ∫b	dy ∫ f (x, y)dx + ∫c		dy ∫ f (x, y)dx.
d	x1 (y)	b	x2 (y)

Рис. 4

В случае более сложного контура область S разбивается на конечное число частей рассмотренных типов.

						1 2	dxdy
	1.1.	Вычислить двойные		интегралы: а) ∫∫0 1				;
	1.1.	Вычислить двойные		интегралы: а) ∫∫0 1			(x + y)2	;
		e y		π		2cosϕ
2	x	e y		; г) ∫2		2cosϕ
б) ∫dx∫		(x2 −2 y +1)dy ; в) ∫∫ ydxdy		; г) ∫2	dϕ	∫ ρ3d ρ .
1	0	1 1	x	π		0
				− 2

Решение. а) Поскольку пределы интегрирования постоянные величины, то первое интегрирование может быть по любой переменной. Запишем интеграл в виде

∫0 dx∫1

(x + y)2

Вычислим внутренний интеграл по у, считая, что х посто-

янная величина

−

∫0

dx = −

∫0

−

dx .

x + y

x +2

x +1

Далее вычисляем внешний интеграл по х

x +1

−

=ln

x +1

−ln

x +2

=ln

−ln

=ln

∫0 x +1

x +2

б) Поскольку пределы внутреннего интеграла зависят от х,

то вычисляем сначала внутренний интеграл по у, считая х постоянной величиной

∫2 ((x2 y − y2 + y)			0x )dx = ∫2 (x3 − x2 + x)dx .
∫2 ((x2 y − y2 + y)			0x )dx = ∫2 (x3 − x2 + x)dx .
1						1
Далее находим внешний интеграл												2
2					4		x	3		x	2
2					4			3			2
∫	(x3 − x2 + x)dx =			x		−			+				=	35 .
∫	(x3 − x2 + x)dx =					−			+				=	35 .
1			4			3			2			1		12
1			4									1
		4

в) Поскольку пределы внутреннего интеграла зависят от у, то интегрируем сначала по х, считая у постоянной величиной, а затем интегрируем по у

∫∫

dxdy = ∫dy

∫

dx = ∫y ln x

= ∫e

y ln ydy =

ln y

−

∫e

ydy

dy =

= e24+1.

г) Вычислим сначала внутренний интеграл

2cosϕ

∫2

dϕ =4 ∫2

cos4 ϕdϕ = ∫2

dϕ ∫

ρ3dρ =

ρ4

(1+cos2ϕ)2 dϕ =

−2

−

−2

(1+cos4ϕ)

dϕ

2cos2ϕ+

ϕ+sin 2ϕ

sin 4ϕ

π.

∫π

−2

−π

1.2. Вычислить двойные интегралы:

а) ∫∫x cos (x + y)dxdy, где D

≤ x ≤π, 0 ≤ y ≤

;

= 0

б) ∫∫(x + y)dxdy,

где D ={y = 0,

y = x2 , x = 2};

в) ∫∫xydxdy, где D ={y = −x, y = x2 , y =1};

г) ∫∫xdxdy, где область D ограничена осью Ox и одной аркой

циклоиды x = a (t −sin t ), y = a (1−cos t ).

Решение. а) Расставим пределы интегрирования и проинтегрируем сначала по у, а затем по х

				π		π
∫∫x cos (x + y)dxdy = π∫xdx∫2 cos (x + y)dy = π∫x sin (x + y)						2 =
D			0	0	0	0
D			0	0	0	0
π	π				π
= ∫x sin		+ x	−sin x dx		= ∫x (cos x −sin x)dx =
0	2				0

= π∫x cos xdx −	π∫x sin xdx = x sin x −		π∫sin xdx + x cos x −	π∫cos xdx =
0	0		0	0
= (x sin x +cos x + x cos x −sin x)		π	= −1−π −1 = −(2 +π ).
= (x sin x +cos x + x cos x −sin x)		π	= −1−π −1 = −(2 +π ).
		0
		0

б) Представим область интегрирования на рис 16.5. Расставим пределы интегрирования и проинтегрируем

	2	x2	2	y	2	x2

∫∫(x + y)dxdy = ∫dx ∫(x + y)dy = ∫ xy +						dx =
				2
D	0	0	0			0

	2		3		x4		x4				x5	2	16		36

=		x		+		dx =			+			= 4 +		=		.

	∫0				2			4		10		0	5		5

Рис. 5

в) Сделаем чертеж (рис. 6).

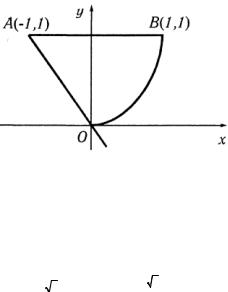
Рис. 6

Из совместного решения уравнений y = −x и y = x2 нахо-

дим точки пересечения прямой и параболы А (-1, 1), О (0, 0). Координаты точки В(1,1). Расставим пределы интегрирования и проинтегрируем

∫∫xydxdxy = ∫1						y		1	∫1					y			1	∫1	(y2	− y3 )dy =
														y

				ydy ∫ xdx =							yx2				dy =
D		0				−y		2	0					−y			2	0
	1		y3			y4	1	1		1			1			1
	1		y3			y4	1	1		1			1			1
=					−		=					−			=		.
=	2	3			−	4	=			3		−			=	24	.
	2	3				4	0	2		3			4			24
							0

г) Для одной арки циклоиды параметр t изменяется от 0 до 2π , а переменная х от 0 до 2πa . Представляя функцию у в виде функции от х у =f(x), запишем искомый интеграл, разделяя переменные

	2∫πa xdx	y= f (x)
I = ∫∫xdxdy =	2∫πa xdx	∫ dy .
D	0	0

Находя дифференциалы dx = a (1−cos t )dt, dy = a sin tdt и переходя во внешнем интеграле к переменной t, получим

2∫π a(t −sint)a(1−cost)dt

a(1−cost)

2∫π (t −sint)(1−cost)2 dt =

I =

∫

dy =a3

=a3

2∫π (t −2t cost +t cos2 t −sint +sin 2t −sint cos2 t)dt =

−2t sint −2cost +

t +

sin 2t

−

cos2t

	1		1	3		2π	2 3

+cost −		cos2t +		cos	t	=3π	a .
	2		3
						0

1.3. Изменить порядок интегрирования в двойных

2	x+2	2	2−y
интегралах: а) ∫dx ∫		f (x, y)dy ; б) ∫dy	∫ f (x, y)dx ;
−1	x2	−6	y2	−1
			4	−1
			4
Решение. а) По пределам интегрирования строим область

интегрирования: у = х + 2, у = х2, х = 2, х = -1 (рис. 7). Решая совместно уравнения у = х + 2, у = х2, находим координаты точек пересечения прямой и параболы А (-1, 1), В (2,4).

Рис. 7

Поскольку слева область D ограничена линиями x = y −2 и x = − y , а справа x = y , то при изменении порядка интег-

рирования интеграл разбивается на два интеграла, соответственно, по областям DACOA и DABC

∫2 dxx∫+2	f (x, y)dy = ∫1	y		y
∫2 dxx∫+2	f (x, y)dy = ∫1	dy ∫ f (x, y)dx +∫4		dy ∫ f (x, y)dx .
−1 x2	0	− y	1	y−2

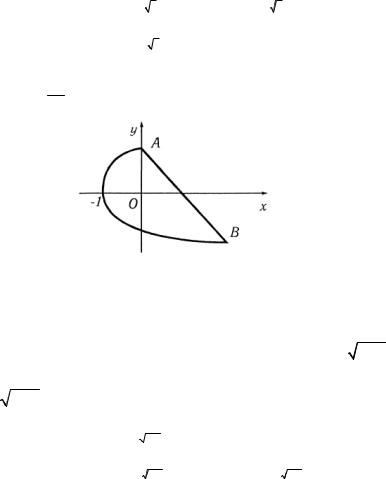
б) Область интегрирования D ограничена линиями

x = 2 − y, x = y2 −1, y = 2, y = −6 (рис. 8). 4

Рис. 8
Решая совместно уравнения x = 2 − y и x =	y2	−1, находим
Решая совместно уравнения x = 2 − y и x =	4	−1, находим
	4

координаты точек пересечения прямой и параболы А (0, 2) и В

(8, - 6). Сверху область D ограничена линиями:								y = 2 x +1
при −1 ≤ x ≤ 0 и y = 2 − x				при	0 ≤ x ≤8 , а снизу –			параболой
y = −2		x +1 . Следовательно, при изменении порядка интегри-
рования интеграл разбивается на два
2	2−y		0	2 x+1	8	2−x
∫dy	∫		f (x, y)dx = ∫dx	∫	f (x, y)dy +∫dx	∫	f (x, y)dy .
−6	y2	−1	−1	−2 x+1	0	−2 x+1
	4	−1
	4

2. Двойной интеграл в полярных координатах. Замена переменных в двойном интеграле

1°. При переходе в двойном интеграле от прямоугольных координат к полярным необходимо в подынтегральном выражении прямоугольные координаты заменить полярными по

1 / 61 2 3 4 5 6 > Следующая >>>

Соседние файлы в предмете Высшая математика