Учебное пособие 792

среднюю квадратическую ошибку выборкиμ .Для повторной выборки по формуле (7), в которой n= 100, получим

бесповторная, то δ =3 0,150897 = 0, 45269 ц.

Таким образом, средняя урожайность при повторной выборке на всем поле с вероятностью 0,9973 находится по формуле (3) и заключена в границах

x −δ ≤ X ≤ x +δ; 14, 4 −0, 48 ≤ X ≤14, 4 +0, 48 ; 13,92 ≤ X ≤14,88;

если выборка бесповторная

14, 4 −0, 45 ≤ X ≤14, 4 +0, 45;

13,95 ≤ X ≤14,85.

5.8. В партии из 10000 лампочек было проверено 1000 лампочек .Среди проверенных оказалось 5% бракованных. Найти: а) при повторной и бесповторной выборке вероятность того, что доля бракованных лампочек во всей партии отличается от их доли в выборке не более чем на 0,01.

б) границы, в которых с вероятностью 0,9836 заключена доля бракованных лампочек во всей партии.

Решение. а) Средняя квадратическая ошибка при повторной выборке при доле бракованных лампочек в выборке w=0,05 по формуле (9) равна

30

при бесповторной выборке и объеме генеральной совокупности N=10000 равна

б) По таблице (3) находим, что Ф(2,4) = 0,9836; откуда t = δμ = 2, 4.

Средняя квадратическая ошибка, если выборка повторная, μ = 0,00689, а, если выборка бесповторная, μ = 0,0065364.

Таким образом, предельная ошибка для повторной выборки

δ = 2, 4 0,00689 = 0,0165;

для бесповторной

δ = 2, 4 0,0065364 = 0,0157.

Границы, в которых с вероятностью 0,9836 заключена доля бракованных лампочек, для повторной выборки равна

0,5 −0,0165 ≤ P ≤ 0,5 +0,0165;

0, 4835 ≤ P ≤ 0,5165.

5.9. При каком объеме повторной выборки можно утверждать с вероятностью 0,9836, что отклонение выборочной средней от генеральной не превыситδ = 0,2, если

σ = 0,9?

Решение. Из выражения (6) имеем

31

P (X − x ≤ 0,02)= 2Ф(t )= 0,9836,

откуда по таблице (3) t = 2,4. Поскольку выборка повторная, то полагая σ sn по формуле (11) ее объем равен

5.10. Из партии в 1000 деталей для определения доли брака производится выборка. Найти объем выборки, при котором с вероятностью Р = 0,9973 гарантируется ошибка не свыше 0,2, если: а) выборка повторная; б) выборка бесповторная и вероятность изготовления бракованных деталей равна q= 0,2.

Решение. В условии нет значения доли брака, поэтому при

определении объема выборки в формуле(13) n = t2 pq следует

δ2

использовать наибольшее значение pq = 0,25.

Таким образом, учитывая, что при заданной вероятности по

5.11. При изучении физико-механических свойств ткани было испытано n =12 образцов и получены следующие

значения предела прочности на разрыв H / мм2 : 19,5;16,8;17,1;17,5; 15,7; 15,5; 14,6; 20,0; 19,4; 18,2; 16,2; 19,2.

Требуется: а) найти выборочное среднее x , «исправленное» стандартное отклонение s (x) и коэффициент вариации υ

изучаемого признака; б) найти доверительный интервал для среднего предела прочности а этой ткани на уровне заданной надежности у = 0,95.

32

Решение. а) Вычисления будем вести в табличном виде. Запишем результаты наблюдений в столбец 1 таблицы и

Коэффициент вариации υ изучаемого признака

33

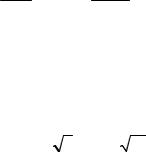
υ = s (xx) 100% = 17,1, 7948 100% =10, 24%.

б) Для заданной доверительной вероятности γ = 0,95 и

Искомый 95% -ный доверительный интервал для ожидаемого предела прочности а исследуемой ткани

Таким образом, средний предел прочности ткани находится в интервале от 16,34H / мм2 до 18,62H / мм2.

5.12. С целью определения размеров детской одежды проведено выборочное обследование детей и получено следующее распределение количества детей по величине обхвата груди

σB , коэффициент вариацииυ изучаемого признака; в) найти

доверительный интервал для ожидаемого среднего значения а обхвата груди на уровне надежности γ = 0,9108, вероятность

того, что величина признака X у выбранного случайным образом ребенка окажется в пределах от α = 58 см до β = 66 .

Решение. а) Вычисления будем вести в табличном виде. В

34

рассматриваемой задаче область наблюдаемых значений признака X разбита на w= 6 непересекающихся и одинаковых по длине интервалов (столбец 1). В столбце 2 приведено распределение числа nk наблюдений по этим интервалам

Построим гистограмму относительных частот для наблюдаемых значений признака X. Для этого определим среднее значение xk признака Z для каждого k-го интервала по

формуле xk = 12 (xH (k )+ xB (k )), где xH (k ) и xB (k ) — нижняя

и верхняя границы k-го интервала. Полученные значения xk внесем в столбец 3.

Вычислим относительную частоту wk = nnk попадания

величины признака Х в k-ый интервал, где nk - число наблюдений в k-м интервале; n = ∑nk - общее число наблюдений. Полученные значения wk внесем в столбец 4. Проверка ∑wk =1. Гистограмма относительных частот показана на рис. 10.

35

Доверительный интервал для ожидаемого среднего значения а обхвата груди у детей рассматриваемой группы

Будем полагать, что случайная изменчивость признака X описывается законом нормального распределения с параметрами a и σ , и воспользуемся точечными оценками величин этих параметров: a 64,13 и σ σB = 4,09.

Используя соотношение

P (α < X < β)=Ф βσ−α −Ф ασ−a

и учитывая нечетность функции Лапласа, имеем

=Ф(0, 46)+Ф(1,5)= 0,1772 +0, 4332 = 0, 6104.

6.Моменты, асимметрия и эксцесс

1°. Моментом к-го порядка называется среднее арифметическое из к-х степеней отклонений значений признака от С

νk = (∑ni (xi −C )k )/ n,

где xi - наблюдаемая варианта; ni —частота варианты;

n = ∑ni —объем выборки; С—произвольное постоянное

число.

Если С = О, то момент называется начальным . Нетрудно заметить, что начальный момент первого порядка есть выборочная средняя

Если С = x , то момент называется центральным порядка к

μx = (∑ni (xi − x )k )/ n.

37

Нетрудно заметить, что центральный момент первого порядка равен нулю, а центральный момент второго порядка равен дисперсии.

Между центральными и начальными моментами существует зависимость

μ2 =ν2 −ν12 ;

2°. Асимметрия распределения определяется равенством

и является показателем отклонения распределения признака X от симметрии относительно x. При α = 0 —распределение симметрично.

3°. Эксцессом называется величина

Найти асимметрию и эксцесс.

Решение. Начальные моменты первого, второго, третьего и четвертого порядков данного распределения находим, пользуясь расчетами в табличном виде

38

Отсюда ν1 = 1220 = 0,6; ν2 = 5620 = 2,8; ν3 =17420 =8,7; ν4 = 40,6.

Центральные моменты вычисляем по формулам (1):

μ2 = 2,8 −(0,6)2 = 2, 44; μ3 =8,7 −3 0,6 2,8 +2(0,6)3 = 4,092;

μ4 = 40,6 −4 0,6 8,7 +6(0,6)2 2,8 −3(0,6)4 = 25,3792.

7. Условные варианты. Метод расчета сводных характеристик выборки

1°. Равностоящими называются варианты, которые образуют арифметическую прогрессию с одинаковой разностью h между любыми двумя соседними вариантами.

Условными называются варианты, определяемые по формуле

39