
Учебное пособие 792
.pdfxi |
0,02 |
0,03 |
0,07 |
ni |
2 |
5 |
3 |
Решение. С целью упрощения расчетов переходим в распределении к целым числам посредством условных вариант ui =100xi
ui |
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
7 |
|
ni |
|
|
2 |
|
|
|
|
|
|
5 |
|
|
|
|
|
3 |
|
Исправленную выборочную дисперсию условных вариант |
|||||||||||||||||
находим по формуле (7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
su2 = 1 |
|
|
|
|
49 − (2 |
2 +5 3 +3 7) |
2 |
|
|
40 |
|||||||
2 4 +5 |
9 +3 |
|
|
|
= |
||||||||||||
9 |
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Искомая исправленная дисперсия находится по формуле |
|||||||||||||||||
|
|
s2 = |
|
s2 |
= |
40 |
|
|
= |
1 |
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
C2 |
|
9 1002 |
2250. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3.6. В результате испытания некоторого параметра получено распределение
170-190 |
190-210 |
210-230 |
230-250 |
250-270 |
10 |
11 |
12 |
9 |
8 |
Найти дисперсию, коэффициент вариации и размах вариации признака.
Решение. Необходимые вычисления приведем в виде таблицы
20

|
интервал |
|
n |
|
|
Середина |
u = x −220 |
n u |
|
||
|
|
|
|
i |
|
|
интервала |
i i |
i i |
|
|
|
170-190 |
|
|
10 |
|
|
180 |
-40 |
-400 |
|
|
|
190-210 |
|
|
11 |
|
|
200 |
-20 |
-220 |
|
|
|
210-230 |
|
|
12 |
|
|
220 |
0 |
0 |
|
|
|
230-250 |
|
|
9 |
|
|
240 |
20 |
180 |
|
|
|
250-270 |
|
|
8 |
|
|
260 |
40 |
320 |
|
|
|
сумма |
|
|
50 |
|
|
|
|
|
-120 |
|
|
|
|
x = x |
|
= ∑niui |
= 220 −2, 4 = 217,6. |
|
|
|||
|
|
|
|
0 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Искомую выборочную дисперсию находим по формуле |
||||||||||
D = ∑niui − ∑niui 2 |
=10 1600 +11 400 +9 400 +8 1600 −2, 42 = 730,34. |
||||||||||
|
n |
|
n |
|
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Среднее квадратическое отклонение равно |
|
|
|||||||||
|
|
|
|
|
|
|
σ = |
D = 27,0248. |
|
|
|
Отсюда коэффициент вариации
ν= σx 100% =12, 419,
а ее размах
R = xmax − xmin = 270 −170 =100.
4. Мода и медиана
1°. Модой называется варианта с наибольшей частотой, т.е. наиболее часто встречающееся значение признака.
Если интервалы вариационного ряда имеют постоянную ширину h, то мода признака определяется по формуле
nm −nm−1 |
|
M0 = xm +h (nm −nm−1 )+(nm −nm+1 ), |
(1) |
где xm — начальное значение модального интервала, nm — наибольшая частота, nm−1 и nm+1 — частота интервала предшествующего и последующего модальному.
21

2°. Медианой называется варианта, которая делит статистическую совокупность на две равные части по числу вариант.
Медиана признака в случае интервального распределения определяется по формуле
|
|
|
|
n |
−γ |
e−1 |
|
|
M |
e |
= x |
+h |
2 |
|
, |
(2) |
|
|
|
|
||||||
|
e |
ne |
|
|
|
|||
|
|
|
|
|
|
|
|
|
где п — объем статистической совокупности, γe−1 накопленная частота до е-го интервала, ne — частота е-го интервала, е —
номер медианного интервала определяется из условия γe−1 ≤ n |
|||||||||||||||
|
|
|
> n |
|
|
|
|
|
|
|
|
|
|
|
2 |
и |
γ |
e+1 |
, x |
— начальное значение медианного интервала. |
|||||||||||
|
|
2 |
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.1. Дано интервальное распределение |
|
|
|||||||||||
|
8-11 |
|
|
11-14 |
|
14-17 |
|
17-20 |
20-23 |
23-26 |
|||||
|
|
5 |
|
|
|
11 |
|
32 |
|
18 |
|
17 |
6 |
||
|
|
Найти |
моду и медиану. |
|
|
|
|
|
|
|
|||||
|
|
Решение. |
Наибольшей |
частоте nm =32 соответствует |
|||||||||||
интервал |
|
14—17. |
Воспользуемся |
формулой (1). |
Так как |
||||||||||
h =3; xm =14; nm−1 =11; и nm+1 =18, то |
|
|
|
|
|
||||||||||
|
|
|
M0 =14 +3 |
|
32 −11 |
|
|
=14 |
+1,8 =15,8. |
|
|||||
|
|
|
(32 −11)+(32 −18) |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Для нахождения медианы строим кумулятивный ряд |
|||||||||||||
|
8-11 |
|
|
11-14 |
|
14-17 |
|
17-20 |
20-23 |
23-26 |
|||||
|
|
5 |
|
|
|
16 |
|
48 |
|
66 |
|
83 |
89 |
||
В |
нашем |
|
случае |
n |
= 44,5, поэтому |
|
медианным интервалом |
||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
является интервал 14-17.Медиану находим по формуле (2) |
|||||||||||||||
|
|
|
|
|
|
Me =14 +3 44,5 −16 |
16,67. |
|
|||||||
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
22

5. Доверительные интервалы для средних. Выборочный метод
1°. Пусть требуется оценить по данным выборки некоторый параметр. При выборке малого объема пользуются точечными и интервальными оценками. Точечной называется оценка, которая определяется одним числом. При точечном оценивании предполагается, что истинное значение параметра генеральной совокупности приблизительно равно соответствующей выборочной характеристике. Так, выборочное среднее x служит точечной оценкой величины генеральной средней x2 и т. д. Под интервальной оценкой
будем понимать интервал, который покрывает оцениваемый параметр. Интервал, покрывающий оцениваемый параметр с заданной надежностью γ , (доверительной вероятностью),
называется доверительным.
Доверительный интервал для оценки математического ожидания а нормально распределенной величины по
выборочной |
средней |
x |
при |
известном |
среднем |
||||
квадратриеском |
отклонении |
σ |
генеральной совокупности |
||||||
определяется неравенством |
|
|
|
|
|
|
|||
|
x −t |
σ |
< a < x +t |
σ |
, |
(1) |
|||
|
|
n |
|||||||
|
|
n |
|
|
|
|
|
||
где п — объем выборки, |
t |
— значение аргумента функции |
|||||||
Лапласа Ф(t )= γ . Значение |
t |
определяется по |
таблице |
||||||
|
2 |
|
|
|
|
|
|
|
|
функции Лапласа по заданной надежности γ .
Точность оценки или средняя ошибка выборки, с которой доверительный интервал покрывает неизвестный параметр а,
определяется по формуле |
|
σ =tσ / n. |
(2) |
Доверительный интервал для оценки математического ожидания нормального распределения при неизвестном среднем квадратическом отклонении о генеральной
23

совокупности по выборочной средней |
x |
и объеме выборки |
|||
n>30 определяется неравенством |
|
|
|
||
x −tγ |
s |
< a < x +tγ |
s |
, |
(3) |
|
n |
||||
|
n |
|
|
||
где S — исправленное среднее квадратическое отклонение, значение tγ находится при заданных n иγ по таблице (4).
Доверительные интервалы для оценки среднего квадратического отклонения а нормального распределения количественного признака Z генеральной совокупности с надежностью у по исправленному выборочному среднему квадратическому отклонению S определяются неравенствами
s (1−q)<σ < s (1+q) |
при q<1; |
(4) |
0 <σ < s (1+q) |
при q>0, |
(5) |
где значения q находятся по таблице (5) по заданным n и |
γ . |
|
2°. Выборочный метод позволяет по данным выборочного обследования определить признаки, характеризующие генеральную совокупность.
Пользуясь теоремой Лапласа
P ( |
|
|
|
≤δ )= 2Ф |
δ |
, |
(6) |
X |
− x |
||||||
|
|
|
|
|
μ |
|
|
|
|
|
|
|
|
||
где X — генеральная средняя, μ — средняя квадратическая ошибка выборки, можно найти:
1)какова вероятность того, что отклонение генеральной средней от выборочной не превышает заданного значения δ ;
2)при каком объеме выборки n выполнима заданная
точность того, что отклонение генеральной средней X от выборочной x не превышает определенного числа;
3) в каких границах заключена генеральная средняя, если известна вероятность того, что отклонение генеральной средней от выборочной удовлетворяет соответствующему отклонению.
Для случайной повторной выборки при определении средней признака величина μ определяется по формуле
24
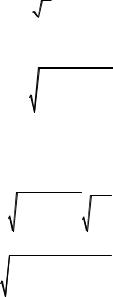
|
|
μ = |
sn |
, |
|
|
|
|
(7) |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
n |
|
|
|
|
|
|
где sn |
2 —дисперсия случайной величины в выборке; для |
|||||||||
бесповторной выборки |
|
|
|
|
|
|
|
|
||
|
|
μ = |
|
s 2 |
|
n |
|
|
||
|
|
|
n |
1− |
|
|
, |
(8) |
||
|
|
|
n |
|
||||||
|
|
|
|
|
N |
|
|
|||
где |
1−n / N - |
необследованная |
часть |
генеральной |
||||||
совокупности. |
|
|
|
|
|
|
|
|
|
|
Для случайной повторной выборки при определении доли
признака |
( |
|
) |
|
|
|
|
pq |
|
|
||
|
−w |
|
|
|
|
|
|
|||||
μ = |
|
w 1 |
|
|
|
|
|
|
|
|
(9) |
|
|
n |
|
|
|
|
n , |
||||||
|
|
|
|
|
||||||||
для бесповторной выборки. |
|
|
|
|
|
|
|
|
|
|
||
μ = |
w(1−w) |
|
|
− |
|
n |
|
(10) |
||||
|
|
|
1 |
|
|
|
, |
|||||
|
n |
|
|
|
||||||||
|
|
|
|
|
|
N |
|
|
||||
где w и 1−w — доли данного и противоположного признака в выборке.
Если требуется определить необходимый объем выборки с заданной точностью Р=2Ф(t), то разрешая формулы (7), (8) относительно n для повторной выборки получим
n = |
t2 s2 |
; |
|
(11) |
|||
|
n |
|
|||||
δ2 |
|||||||
для бесповторной |
|
|
|
|
|||
|
|
|
|
|
|
||
n = |
|
Nt2s2 |
(12) |
||||
Nδ |
2 +t2s2 ; |
||||||
|
|
|
|
n |
|
||
n
Разрешая относительно n(9), (10) при определении доли признака, для повторной выборки получим
n = |
t2 w(w −1) |
; |
|
(13) |
||
δ2 |
|
|||||
для бесповторной |
|
|
|
|
||
|
|
|
|
|
||
n = |
|
N t2 p q |
|
. |
(14) |
|
Nδ2 +t2 p q |
||||||
|
|
|
||||
25

5.1. Найти доверительный интервал для оценки математического ожидания нормально распределенной величины с надежностью 0,95, если известно генеральное среднее квадратическое отклонение σ = 4, объем выборки n = 36 и выборочная средняя x = 8.
Решение. Для нахождения доверительного интервала воспользуемся формулой (1). Значение t находим из
соотношения |
Ф(t )= γ |
= 0, 475 по |
таблице (3): t - 1,96. |
|||
|
|
2 |
|
|
|
|
Подставив все значения в формулу (1), получим |
||||||
8 |
−1,96 |
4 |
|
< a <8 +1,96 |
4 |
; |
36 |
|
36 |
||||
|
|
|
|
|
||
6,794 < a <9, 206.
5.2. Известно среднее квадратическое отклонение σ = 3 Нормально распределенной генеральной совокупности. Найти с надежностью 0,95: а) минимальный объем выборки, если точность оценки математического ожидания генеральной совокупности по выборочной средней равна σ = 0, 2;
б) точность σ , с которой выборочная средняя оценивает математическое ожидание, если выборка объема n = 100.
Решение. а) Для определения минимального объема
выборки воспользуемся формулой (2) |
n = |
t2σ2 |
.По условию |
|
δ2 |
||||
|
|
|
γ = 0,95, тогда Ф(t )= 0, 475 и по таблице (3) находим t = 1,96.
Искомый объем выборки n = |
1,962 |
32 |
1,96 3 |
2 |
||||
(0, 2) |
2 |
; |
n = |
0, 2 |
|
=869. |
||
|
|
|
|
|
|
|||
б) Для определения точности оценки математического ожидания генеральной совокупности по выборочной средней воспользуемся формулой (2). Поскольку при γ = 0,95
26

значения t =1,96, то точность оценки выборки объема и = 100
равна δ =1,96 |
3 |
= 0,588. |
|
|
|
||
100 |
|
|
|
||||
|
|
|
|
|
|
|
|
5.3. Из генеральной совокупности извлечена выборка |
|
||||||
|
|
|
|
|
|
|
|
xi |
|
2 |
|
3 |
5 |
|
8 |
ni |
|
2 |
|
3 |
6 |
|
4 |
Оценить с надежность 0,99 математическое ожидание нормально распределенного признака генеральной совокупности по выборочной средней.
Решение. Математическое ожидание будем оценивать при помощи доверительного интервала. Поскольку среднее квадратическое отклонение генеральной совокупности неизвестно, то для оценки математического ожидания воспользуемся формулой (3). Выборочную среднюю находим по формуле
x = ∑ni xi / n = (2 2 +3 3 +6 5 +4 8)/15 = 5.
Исправленное среднее квадратическое отклонение находим по формуле
s = ∑ni (xi − x )2 / (n −1) = |
|
= ((2(2 −5)2 +3(3 −5)2 +6(5 −5)2 +4(8 −5)2 )/14)1/ 2 |
= 2,1679. |
Пользуясь таблицей (4) по γ = 0,99 и |
n =15 находим |
tγ = 2,98. |
|
Подставляя найденные величины в формулу (3), получим искомый доверительный интервал
5 −2,98 2,167915 < a < 5 +2,98 2,167915 ;
3,3319 < a < 6,6681.
27

5.4. По данным 7 независимых испытаний физической величины найдено среднее арифметическое результатов отдельных измерений x = 50,7 и исправленное среднее квадратическое отклонение s = 4,5. Оценить истинное значение измеряемой величины с надежностью γ = 0,99 .
Решение. Истинное значение измеряемой величины равно ее математическому ожиданию. Следовательно, решение сводится к оценке математического ожидания при неизвестном среднем квадратическом отклонении генеральной совокупности. Рассматривая число измерений, как объем выборки, математическое ожидание (истинное значение измеряемой величины) оценим при помощи доверительного интервала по формуле (3). Значение tγ определяем по таблице
(4) приγ = 0,99 и n = 7 : tγ =3,71.
Подставляя все величины в формулу (3), получим
50,7 −3,71 4,57 < a < 50,7 +3,71 4,57 ;
44,389 < a <57,01.
5.5. По выборке объема n = 12 из генеральной совокупности найдено исправленное среднее квадратическое
отклонение |
s = 1,2 |
нормально |
распределенного |
|
количественного признака X. Найти доверительный интервал, |
||||
покрывающий |
генеральное |
среднее |
квадратическое |
|
отклонение σ с надежностью 0,95. |
|
|
||
Решение. Доверительный интервал в данном случае находится по формуле (4) или (5) в зависимости от q. Так как при γ = 0,95 и n =12 по таблице (5) q = 0,55 < 1, то искомый
доверительный интервал находим по формуле (4) 1, 2(1−0,55)<σ <1, 2(1+0,55);
0,54 <σ <1,86.
5.6. Найти точность прибора с надежностью 0,99, если по 8 равноточным измерениям некоторой величины найдено, что исправленное среднее квадратическое отклонение равно
S = 0,25. 28
Решение. Точность прибора определяется средним квадратическим отклонением σ случайных ошибок измерений. Найдем доверительный интервал, покрывающий σ с заданной надежностью γ = 0,99 .Поскольку при γ = 0,99 и
n = 8 таблице (5) значение q = 1,38 > 1, то воспользуемся неравенством (5)
0 <σ < 0, 25(1+1,38); 0 <σ < 0,595.
5.7. Результаты урожайности риса на различных участках поля площадью 1000 га приведены в следующей таблице
урожайность |
10-12 |
12-14 |
14-16 |
16-18 |
|
|
|
|
|
в ц. с га |
|
|
|
|
количество |
15 |
20 |
45 |
20 |
га |
|
|
|
|
Найти: а) при повторной и бесповторной выборке вероятность того, что средняя урожайность риса на всем поле отличается от средней выборочной не более чем на 0,1 ц ; б) границы, в которых с вероятностью 0,9973 заключена урожайность на всем поле.
Решение. а) Принимая за значение признака середины интервалов, найдем среднюю арифметическую и дисперсию заданного в условии распределения
|
x = |
∑ni xi = |
15 11+20 13 |
+45 15 +20 17 |
=14, 4; |
|
||
|
|
n |
|
|
15 +20 |
+45 +20 |
|
|
s2 |
= ∑ni (xi − x )2 |
= |
15(−3,5)2 +20(−1,5)2 +45(0,5)2 +20(2,5)2 |
= 2,53. |
||||
|
||||||||
n |
n |
|
|
|
|
99 |
|
|
|
|
|
|
|
|
|
||
При определении вероятности искомого события воспользуемся формулой (6), в которой δ = 0,1. Найдем
29
