
Численные методы. методические указания для организации самостоятельной работы по курсу Высшая математика. Пантелеев И.Н
.pdf
ФГБОУ ВПО «Воронежский государственный технический университет»
Кафедра высшей математики и физико-математического моделирования
267 - 2013
ЧИСЛЕННЫЕ МЕТОДЫ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ для организации самостоятельной работы
по курсу "Высшая математика" для студентов направления 280700.62 «Техносферная безопасность»,
профили «Защитавчрезвычайныхситуациях», «Безопасность жизнедеятельностивтехносфере», «Защитаокружающейсреды», очной формы обучения
Воронеж 2013
Составитель канд. физ.-мат. наук И.Н. Пантелеев
УДК 681.3.06
Численные методы: методические указания для организации самостоятельной работы по курсу "Высшая
математика" |
для |
студентов |
направления |
280700.62 |
|
«Техносферная |
|
безопасность», |
профили «Защита |
в |
|
чрезвычайных ситуациях», «Безопасность жизнедеятельности в техносфере», «Защита окружающей среды», очной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; сост. И.Н. Пантелеев. Воронеж, 2013. 47 с.
Настоящие методические указания предназначены в качестве руководства для организации самостоятельной работы по курсу "Высшая математика" при изучении во 2 семестре раздела «Численные методы» для студентов специальностей ЧС, БЖ и ЗС. В работе приведен теоретический материал, необходимый для выполнения заданий и решения типовых примеров.
Методические указания подготовлены на магнитном носителе в текстовом редакторе Microsoft Word 2003 и
содержатся в файле Vmfmm_ChMetLab1.pdf.
Ил. 9. Библиогр.: 11 назв.
Рецензент канд. физ.-мат. наук, доц. В.В. Ломакин Ответственный за выпуск зав. кафедрой д-р физ.-мат. наук, проф. И.Л. Батаронов
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
ФГБОУ ВПО «Воронежский государственный технический университет», 2013
ЛАБОРАТОРНАЯ РАБОТА № 1
ОПЕРАЦИИ С ВЕКТОРАМИ И МАТРИЦАМИ
1. Создание единичной матрицы
Для создания единичной матрицы (она обычно обозначается E ) служит функция eye :
- eye n – создает единичную матрицу размера n n ;
- eye n, m – создает матрицу размера n m с единицами по диагонали и нулями в остальных ячейках;
- eye size A – создает единичную матрицу того же размера,
что и матрица A .
Единичная матрица не определена для многомерных массивов. Так, функция E eye 2,3, 4 при попытке ее вычис-
ления приведет к ошибке.
Примеры использования функции eye :
>> E=eye(2,5) |
|
|
||
E = |
|
|
|
|
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
>> E=eye(2,3,4)
??? Error using ==> eye Too many input arguments.
2. Создание матриц с единичными элементами
Для создания матриц, все элементы которых – единицы, используется функция ones :
- ones n – создает матрицу размера n n , все элементы которой – единицы;
- ones n, m – создает матрицу размера n m , состоящую из единиц;
- ones d1, d 2, d3, – создает массив из единиц с размером d1 d 2 d3 ;
- ones size A – создает массив единиц той же размерности,
что и матрица A .
Пример использования функции ones :
>> S=ones(2) S =
1 1
11
3.Создание матрицы с нулевыми элементами
Для создания матриц, все элементы которых – нули, используется функция zeros :
- |
zeros n – создает матрицу размера n n , все элементы ко- |
торой – нули; |
|
- |
zeros n, m – создает матрицу размера n m , состоящую из |
нулей; |
|
- |
zeros d1, d 2, d3, – создает массив из нулей с размером |
d1 d 2 d3 ; |
|
- |
zeros size A - создает массив единиц той же размерности, |
что и матрица A .
Пример использования функции zeros :
>> D=zeros(2,4) D =
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
4. Создание массива равноотстоящих точек |
|
Рассмотрим оператор : (двоеточие). Этот оператор ис- |
пользует следующие правила для создания векторов: |
|
- |
j : k – создает вектор j j 1 j 2 k ; |
- |
j : h : k – создает вектор j j h j 2h k . |
Примеры использования оператора ":" :
>> x=-2:5 x =
2
-2 |
-1 |
0 1 |
2 3 4 5 |
|
|
|
|
>> x=1.5:8 |
|
|
|
|
|
|
|
x = |
|
|
|
|
|
|
|
1.5000 |
2.5000 |
3.5000 |
4.5000 |
5.5000 |
6.5000 |
7.5000 |
|
>> x=-0.6:0.2:1.3 |
|
|
|
|
|
||
x = |
|
|
|
|
|
|
|
-0.6000 |
-0.4000 |
-0.2000 |
0.0000 0.2000 0.4000 0.6000 0.8000 |
||||
1.0000 |
1.2000 |
|
|
|
|
|
|
Функция linspace также формирует линейный массив
равноотстоящих узлов, но в отличие от оператора ":" дает прямой контроль над числом точек. Применяется в следующих формах:
- linspace a,b – создает массив из 100 точек, равномерно распределенных между a и b ;
- linspace a,b, n – создает массив из n точек, равномерно
распределенных в интервале от a до b . Пример использования функции linspace :
>> M=linspace(2,10,7) M =
2.0000 3.3333 4.6667 6.0000 7.3333 8.6667 10.0000
5. Создание массивов со случайными числами
Функция randperm n создает случайные перестановки целых чисел 1: n в матрице-строке. Например:
>> x=randperm(7) |
|
|
|
|||
x = |
|
|
|
|
|
|
2 |
7 |
4 |
3 |
6 |
5 |
1 |
Функция rand генерирует массивы случайных чисел, значения элементов которых равномерно распределены в промежутке 0, 1 :
- rand n – создает матрицу размера n n ;
- rand n, m – создает матрицу размера n m ;
- |
rand d1, d 2, d3, – создает массив из случайных чисел раз- |
|
мером d1 d 2 d3 ; |
||
- |
rand size A |
создает массив той же размерности, что и |
матрица A ;
-rand – создает одно случайное число, которое изменяется при каждом последующем вызове и имеет равномерный закон распределения;
-rand ' state ',0 – сбрасывает генератор случайных чисел в
начальное состояние.
Пример использования функции rand :
>> Y=rand(2,5)
Y=
0.9501 0.6068 0.8913 0.4565 0.8214
0.2311 0.4860 0.7621 0.0185 0.4447
1
0.9 
0.8 

0.7
0.6
0.5

0.4
0.3 
0.2 


0.1
00 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
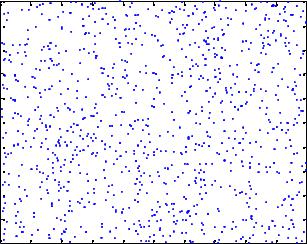
Рис. 1
3 |
4 |
Проверить равномерность распределения случайных чисел можно, построив большое число точек на плоскости со случайными координатами (рис. 1). Это делается так:
>>X=rand(1,1000);
>>Y=rand(1,1000);
>>plot(X,Y,'.')
Функция randn генерирует массив со случайными числами, распределенными по нормальному закону с нулевым математическим ожиданием и среднеквадратическим отклонением равным 1. Разновидности данной функции такие же как и для функции rand . Пример:
>> X=randn(2,5) X =
-0.4326 0.1253 -1.1465 1.1892 0.3273 -1.6656 0.2877 1.1909 -0.0376 0.1746
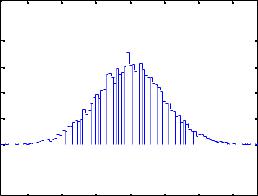
Проверить распределение случайных чисел по нормальному закону можно, построив гистограмму распределения большого количества чисел. Например, следующие команды
>>X=randn(10000,1);
>>hist(X,100)
строят гистограмму (рис. 2) из 100 столбцов для 10000 случайных чисел с нормальным распределением.
400
300
200
100
0 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
Рис. 2
5
6. Создание произвольных массивов
Символы (квадратные скобки) используются для
формирования векторов и матриц. Например:
>> x=[1.3 4.7 sqrt(-1)] x =
1.3000 4.7000 0 + 1.0000i >> X=[1 3 6.7; 2.3 7 9.8]
X=
1.0000 3.0000 6.7000
2.3000 7.0000 9.8000
Здесь точка с запятой разделяет строки массива.
>> Y=[]
Y=
[]
Здесь создается пустая матрица.
7. Арифметические операции над матрицами
Оператор " " выполняет сложение матриц. Оператор " " выполняет вычитание матриц. Оператор "*" выполняет умножение матриц.
Оператор ".*" выполняет поэлементное умножение матрицы на матрицу.
Оператор "^" выполняет возведение матрицы в степень. Оператор ".^ " выполняет поэлементное возведение мат-
рицы в степень.
Оператор "/" выполняет деление матриц слева направо. Оператор "\ " выполняет деление матриц справа налево. Оператор "./" выполняет поэлементное деление матриц
слева направо.
Оператор ". \ " выполняет поэлементное деление матриц справа налево.
Примеры:
>> A=[1 3 6; 2 1 5] A =
1 3 6
6
2 |
1 |
5 |
|
>> B=[1 1 1 1; 2 2 2 2; -1 -1 -1 -1] |
|||
B = |
|
|
|
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
-1 |
-1 |
-1 |
-1 |
>> C=A*B |
|
|
|
C = |
|
|
|
1 |
1 |
1 |
1 |
-1 |
-1 |
-1 |
-1 |
>> D=A.^2 |
|
||
D = |
|
|
|
1 |
9 |
36 |
|
4 |
1 |
25 |
|
a b |
Функция cross a,b вычисляет векторное произведение |
||
в трехмерном пространстве, причем a и b – обязатель- |
|||
но векторы с тремя компонентами. Пример:
>> a=[1 2 3]; b=[3 2 1]; c=cross(a,b) c =
-4 8 -4
8. Суммирование элементов массива
Определены следующие функции суммирования:
- sum A – вычисляет сумму элементов массива, если A -
вектор, или возвращает вектор-строку, содержащую сумму элементов каждого столбца, если A - матрица;
- - sum A, 2 – возвращает вектор-строку, содержащую сумму элементов каждой строки матрицы;
- cumsum A – выполняет суммирование с накоплением. Если A - вектор, то cumsum A возвращает вектор, содержащий результаты суммирования с накоплением элементов вектора A . Если A - матрица, то cumsum A возвращает матрицу то-
го же размера, что и A , содержащую суммирование с накоплением для каждого столбца матрицы A ;
- - cumsum A, 2 – возвращает матрицу того же размера, что и
A , содержащую суммирование с накоплением для каждой строки матрицы A .
Примеры:
>> A=[1 2 3 4; 5 6 7 8; 8 19 11 12]
A = |
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
819 11 12
>>B=sum(A)
B = |
|
|
|
|
|
|
|
|
|
14 |
27 |
21 |
24 |
|
|
|
|
>> B=cumsum(A) |
|
|
|
|
||||
B = |
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
|
|
|
|
|
6 |
8 |
10 |
12 |
|
|
|
|
|
14 |
27 |
21 |
24 |
|
|
|
|
>> B=cumsum(A,2) |
|
|
|
|||||
B = |
|
|
|
|
|
|
|
|
|
1 |
3 |
6 |
10 |
|
|
|
|
|
5 |
11 |
18 |
26 |
|
|
|
|
|
8 |
27 |
38 |
50 |
|
|
|
|
|
|
9. Формирование подматриц из матриц |
|
|||||
- |
A i, j |
– это элемент aij матрицы A ; |
|
|
||||
- |
A :, j |
– это |
j -й столбец из матрицы A ; |
|
|
|||
- |
A i,: – это i -я строка из матрицы A ; |
|
|
|||||
- |
A j : k – это подвектор A j , A j 1 , …, |
A k ; |
||||||
- |
A :, j : k – это подматрица A :, j , A :, j 1 , …, |
A :, k ; |
||||||
- |
A : –записывает все элементы матрицы A в виде столбца. |
|||||||
|
|
Пример: |
|
|
|
|
||
>> A=[1 2 3 4 5 6; 7 8 9 8 7 5; 4 3 2 1 2 3] |
|
|
||||||
A = |
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
7 |
8 |
9 |
8 |
7 |
5 |
|
|
7 |
8 |
4 |
3 |
2 |
1 |
2 |
3 |
>> B=A(:,3:5) |
|
|
|
||
B = |
|
|
|
|
|
3 |
4 |
5 |
|
|
|
9 |
8 |
7 |
|
|
|
2 |
1 |
2 |
|
|
|
10. Матричные операции линейной алгебры
Линейная алгебра – область, в которой наиболее часто используются векторы и матрицы. Наряду с операциями общего характера, рассмотренными выше, применяются функции, решающие наиболее характерные задачи линейной алгебры. Они и рассматриваются в данном пункте:
- |
det A – вычисляет определитель квадратной матрицы A ; |
- |
B orth A – определяет ортонормированный базис матри- |
цы A . Столбцы B определяют то же пространство, что и столбцы матрицы A , но столбцы B ортогональны. Количество столбцов B равно рангу матрицы A . Пример:
>> A=[1 2 3 4 5 6; 7 8 9 8 7 5; 4 3 2 1 2 3] A =
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
8 |
7 |
5 |
4 |
3 |
2 |
1 |
2 |
3 |
>> B=orth(A) B =
-0.4085 0.9123 0.0283 -0.8669 -0.3781 -0.3247 -0.2856 -0.1572 0.9454
- rref A – возвращает приведенную к диагональной или тре-
угольной форме матрицу, используя метод исключения Гаусса с частичным выбором ведущего элемента. Пример:
>> B=rref(A) |
(матрицу А см. выше) |
|
|
||
B = |
|
|
|
|
|
1.0000 |
0 |
-1.0000 |
0 |
4.2000 |
9.4000 |
0 |
1.0000 |
2.0000 |
0 |
-6.0000 |
-13.5000 |
0 |
0 |
0 |
1.0000 |
3.2000 |
5.9000 |
- rrefmovie A – показывает пошаговое исполнение процедуры приведения матрицы к треугольной форме;
- inv A – возвращает матрицу, обратную квадратной матрице
A . Предупреждающее сообщение выдается, если A плохо масштабирована или близка к вырожденной;
- V , D eig A – вычисляет диагональную матрицу D соб-
ственных значений квадратной матрицы A и матрицу V , столбцы которой являются соответствующими собственными векторами. Пример:
>> A=[1 2 3 4; 5 6 7 8; 9 8 7 6; -5 4 3 -2] |
|
||||
A = |
|
|
|
|
|
1 |
2 |
3 |
4 |
|
|
5 |
6 |
7 |
8 |
|
|
9 |
8 |
7 |
6 |
|
|
-5 |
4 |
3 |
-2 |
|
|
>> [V,D]=eig(A) |
|
|
|||
V = |
|
|
|
|
|
0.2381 |
|
0.1736 + 0.3297i |
0.1736 - 0.3297i |
-0.1255 |
|
0.6232 |
|
0.3001 + 0.2741i |
0.3001 - 0.2741i |
0.5647 |
|
0.7249 |
|
0.1429 - 0.4686i |
0.1429 + 0.4686i |
-0.7529 |
|
0.1717 |
|
-0.6753 |
-0.6753 |
0.3137 |
|
D = |
|
|
|
18.2551 |
0 |
0 |
0 |
0 |
-3.1275 + 2.8992i |
0 |
0 |
0 |
0 |
-3.1275 - 2.8992i |
0 |
0 |
0 |
0 |
0.0000 |
-' – транспонирование матриц. Для комплексных матриц транспонирование дополняется комплексным сопряжением;
-.' – транспонирование матриц. Для комплексных матриц операция сопряжения не выполняется.
Примеры:
>> A=[1-i 2 3+2i 4; 5-6i 6+2i 7 8-3i] |
|
|
|
A = |
|
|
|
1.0000 - 1.0000i |
2.0000 |
3.0000 + 2.0000i |
4.0000 |
5.0000 - 6.0000i |
6.0000 + 2.0000i |
7.0000 |
8.0000 - 3.0000i |
>> A' |
|
|
|
ans = |
|
|
|
9 |
10 |
1.0000 |
+ 1.0000i |
5.0000 + 6.0000i |
2.0000 |
|
6.0000 - 2.0000i |
3.0000 |
- 2.0000i |
7.0000 |
4.0000 |
|
8.0000 + 3.0000i |
>> A.' |
|
|
ans = |
|
|
1.0000 - 1.0000i |
5.0000 - 6.0000i |
|
2.0000 |
|
6.0000 + 2.0000i |
3.0000 + 2.0000i |
7.0000 |
|
4.0000 |
|
8.0000 - 3.0000i |
Задание к выполнению лабораторных работ
Внимательно изучите приведенные выше функции и примеры. На собственных примерах освойте применение всех изложенных функций.
Контрольные вопросы
1.Как создавать матрицы различного вида?
2.Как создавать векторы равноотстоящих точек?
3.Какие существуют арифметические операции над матрицами и как они выполняются (численно и аналитически)?
4.Какие математические ограничения вы знаете при применении арифметических операций над матрицами?
5.Как выполняется суммирование элементов массива?
6.Как осуществляется формирование подматриц и подвекторов из матриц и векторов?
7.Какие существуют матричные операции линейной алгебры и как они выполняются (численные и аналитические)?
8.Какие математические ограничения вы знаете при применении матричных операций линейной алгебры?
11
ЛАБОРАТОРНАЯ РАБОТА № 2
ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ y f x . РЕШЕНИЕ УРАВНЕНИЯ f x 0
Довольно часто возникает задача решения нелинейного уравнения вида f x 0 . Данная задача сводится к нахожде-
нию значений аргумента x функции, при котором значение функции равно нулю. При решении этой задачи настоятельно
рекомендуется строить график функции f x для прибли-
женного определения корней и интервалов, в пределах которых они находятся.
Соответствующая функция, решающая задачу нахождения корня уравнения f x 0 , приведена ниже:
- fzero @ fun, x – возвращает уточненное значение x , при
котором достигается нуль функции при начальном значении аргумента x . Возвращенное значение близко к точке, где функция меняет знак или равно NaN (неопределенный числовой результат), если такая точка не найдена;
- fzero @ fun, x1 x2 – возвращает значение x , при котором
достигается нуль функции |
с |
заданием интервала |
поиска |
x1 x2 , такого, что знак f |
x1 |
отличается от знака |
f x2 . |
Если это не так, то выдается сообщение об ошибке. Вызов функции fzero с интервалом гарантирует, что fzero возвратит
значение, близкое к точке, где функция изменяет знак;
- fzero @ fun, x,tol – возвращает результат с заданной погрешностью tol ;
- fzero @ fun, x,tol,trace, p1, p2, – предусматривает дополнительные аргументы, передаваемые в функцию.
12
Для функции fzero ноль рассматривается как точка, где
график функции пересекает ось Ox , а не касается ее. В зависимости от формы задания функции fzero реализуются сле-
дующие хорошо известные численные методы поиска нуля функции: деление отрезка пополам, метод секущей и метод обратной квадратичной интерполяции.
Рассмотрим пример решения уравнения 0,25x sin x1 0 на отрезке 0, 10 .
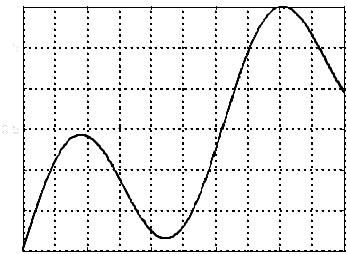
Построим график функции (рис. 3):
>>x=0:0.01:10;
>>plot(x,0.25*x+sin(x)-1);
>>grid on;
Из рисунка нетрудно заметить, что значения корней заключены в интервалах 0, 1 , 2, 3 и 5, 6 . Найдем их, ис-
пользуя функцию fzero :
>>x1=fzero('0.25*x+sin(x)-1',[0 1]) x1 =
0.8905
>>x2=fzero('0.25*x+sin(x)-1',[2 3]) x2 =
2.8500
>>x3=fzero('0.25*x+sin(x)-1',[5 6]) x3 =
5.8128
>>x3=fzero('0.25*x+sin(x)-1',5,0.001) x3 =
5.8111
>>x3=fzero('0.25*x+sin(x)-1',5)
x3 =
5.8128
13
2.0 |
|
|
|
|
|
|
|
|
|
|
|
1.5 |
|
|
|
|
|
|
|
|
|
|
|
1.0 |
|
|
|
|
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
-0.5 |
|
|
|
|
|
|
|
|
|
|
|
-1.0 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|||||||||||
|
|
|
|
|
Рис. 3 |
|
|
|
|
|
|
Обратите внимание, что корень |
x3 найден тремя спосо- |
||||||||||
бами и что его значения в третьем знаке после десятичной |
|||||||||||
точки отличаются в пределах заданной погрешности 0,001. К |
|||||||||||
сожалению, сразу найти все корни |
fzero не в состоянии. |
||||||||||
Решим это же уравнение при помощи функции |
fsolve , |
||||||||||
которая решает уравнение методом наименьших квадратов, |
|||||||||||
ищет не только точки пересечения, но и точки касания. |
|
||||||||||
>> x=fsolve('0.25*x+sin(x)-1',0:10) |
|
|
|
|
|
|
|||||
x = |
|
|
|
|
|
|
|
|
|
|
|
Columns 1 through 8 |
|
|
|
|
|
|
|
|
|||
0.8905 |
0.8905 |
2.8500 |
2.8500 |
2.8500 |
5.8128 |
5.8128 |
5.8128 |
||||
Columns 9 through 11 |
|
|
|
|
|
|
|
|
|||
5.8128 |
10.7429 |
10.7429 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
Задание к выполнению лабораторной работы
|
Решить нелинейное уравнение |
f x g x Cx D 0 |
|||||||||||
на отрезке a, b |
с помощью функций |
fzero и |
fsolve . |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
Вариант |
|
g x |
|
|
|
C |
D |
a, b |
||||
|
1 |
|
|
ex |
|
|
|
-10 |
-35 |
1; 8 |
|
||
|
2 |
|
x3 0,5x2 |
|
|
3 |
6 |
6; 3 |
|
||||
|
3 |
|
arctg x |
|
|
-1 |
2 |
1; 8 |
|
||||
|
4 |
|
|
e x |
|
|
|
11 |
-34 |
8; 1 |
|
||
|
5 |
|
10x |
|
|
|
10 |
-84 |
3; 6 |
|
|||
|
6 |
|
sin x |
|
|
|
0,3 |
-1 |
6; 3 |
|
|||
|
7 |
|
ln x |
|
|
|
-5 |
17 |
1; 10 |
|
|||
|
8 |
|
cos x |
|
|
|
-1 |
3 |
2; 7 |
|
|||
|
9 |
|
|
tg x |
|
|
|
6 |
-12 |
0,6; 1,5 |
|
||
|
10 |
|
arccos x |
|
|
5 |
-4 |
0,1; 1,0 |
|
||||
|
11 |
|
|
tg x |
|
|
|
-3 |
10 |
1; 10 |
|
||
|
12 |
|
arcsin x |
|
|
-6 |
4 |
0,1; 1,0 |
|
||||
|
13 |
|
|
ex2 |
|
|
|
2 |
-10 |
1,0; 1,9 |
|
||
|
14 |
|
arctg |
x |
|
|
-2 |
3 |
0; |
9 |
|
||
|
15 |
|
3x3 2x2 |
|
|
5 |
-6 |
0, 4; 1,3 |
|
||||
|
16 |
|
2ln x 1 x |
|
|
0 |
-1 |
1,8; 2,7 |
|
||||
|
17 |
|
e x x2 |
|
|
0 |
-2 |
1,0; 1,9 |
|
||||
|
18 |
|
|
|
|
|
|
-3 |
3 |
|
|
|
|
|
|
cos x 1 2 |
|
|
1; 2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||
|
19 |
|
102x |
|
|
|
8 |
-80 |
3; 2 |
|
|||
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
20 |
lg x 1 x2 |
0,5 |
0 |
1,0; 1,9 |
21 |
tg x 4 |
-1 |
-3 |
1,0; 1,9 |
22 |
tg x 2 |
6 |
1 |
0,5; 1, 4 |
23 |
sin x 3 |
2,5 |
-2 |
3; 6 |
24 |
2x 2x2 |
0 |
-1 |
0,1; 0,9 |
Контрольные вопросы
1. Каков геометрический смысл решения нелинейного уравнения f x 0 ?
2.Как осуществляется построение графика функции одной переменной?
2.С какой целью используется построение графика функции?
3.Для чего и как используется функция fzero ?
4.Какие численные методы поиска нуля функции вы знаете и как они реализуются?
5.Для чего и как используется функция fsolve ?
6.В чем недостатки и преимущества функций fzero и
fsolve ?
ЛАБОРАТОРНАЯ РАБОТА № 3
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Решение систем линейных уравнений относится к самой массовой области применения матричных методов, рассмотренных в лабораторной работе № 1.
Как известно, обычная система линейных уравнений имеет вид:
16
a11x1 a12 x2 a1n xn b1a21x1 a22 x2 a2n xn b2
...............................................
an1x1 an2 x2 ann xn bn
Здесь a11 , a12 , …, ann – коэффициенты, образующие матрицу
A , которые могут иметь действительные или комплексные значения; x1, x2 , , xn – неизвестные, образующие матрицу-
столбец X ; b1 , b2 , , bn – свободные члены (действитель-
ные или комплексные), образующие матрицу-столбец B . Эта система может быть представлена в матричной форме как AX B . В зависимости от вида матрицы A и ее характерных особенностей MATLAB позволяет реализовать различные методы решения.
Если матрица A квадратная и ее определитель отличен от нуля, то решить систему можно с помощью обратной мат-
рицы X A 1B или методом Гаусса X A \ B . Например:
>> A=[1 2 3; 4 5 6; 7 5 1]
A = |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
5 |
1 |
>>det(A) ans =
6
>>B=[1; 2; 3] B =
1
2
3
>>X1=A\B X1 =
-1.3333 2.6667
-1.0000
>>X2=inv(A)*B X2 =
-1.3333 2.6667 -1.0000
>>X3=A^-1*B X3 =
-1.3333 2.6667 -1.0000
Как и следовало ожидать, результаты оказываются одинаковыми для всех трех способов решения. Сделаем проверку:
>> A*X1 ans =
1.0000
2.0000
3.0000
Задание № 1 к выполнению лабораторной работы
Решить систему уравнений из своего варианта тремя способами, предварительно вычислив определитель матрицы.
Варианты исходных данных
1 |
0,34x1 |
0,71x2 |
0,63x3 |
2,08 |
7 |
3, 75x1 |
0, 28x2 |
0,17x3 |
0, 75 |
||
|
|
0,71x1 |
0,65x2 |
0,18x3 |
0,17 |
|
|
2,11x1 |
0,11x2 |
0,12x3 |
1,11 |
13 |
|
19 |
|
||||||||
|
1,17x |
2,35x |
0, 75x |
1, 28 |
|
0, 22x |
3,17x |
1,81x |
0,05 |
||
|
|
1 |
2 |
3 |
|
|
|
1 |
2 |
3 |
|
2 |
0, 21x1 |
0,18x2 |
0,75x3 |
0,11 |
8 |
0,13x1 0,14x2 |
2,00x3 |
0,15 |
|||
|
|
|
0, 75x2 |
0,11x3 |
2,00 |
|
|
0,75x1 |
0,18x2 |
0,77x3 |
0,11 |
14 |
0,13x1 |
20 |
|
||||||||
|
3,01x |
0,33x |
0,11x |
0,13 |
0, 28x |
0,17x |
0,39x |
0,12 |
|||
|
|
1 |
2 |
3 |
|
|
|
1 |
2 |
3 |
|
3 |
3,01x1 |
0,14x2 |
0,15x3 |
1, 00 |
9 |
0,92x1 0,83x2 |
0,62x3 |
2,15 |
|||
|
|
|
0,13x2 |
0,75x3 |
0,13 |
|
|
|
0,54x2 |
0, 43x3 |
0,62 |
15 |
1,11x1 |
21 |
0, 24x1 |
||||||||
|
0,17x |
2,11x |
0, 71x |
0,17 |
|
0,73x |
0,81x |
0,67x |
0,88 |
||
|
|
|
|
1 |
2 |
3 |
|
||||
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
17 |
18 |
