Методическое пособие 640

ность канала может быть повышена также путем увеличения объема алфавита m, однако при этом возрастает и сложность технической реализации.

5.4. Пропускная способность дискретного канала с помехами

При наличии помех соответствие между множествами символов на входе и на выходе канала связи перестает быть однозначным. Среднее количество информации I(XY), передаваемое по каналу одним символом, определяется в этом случае соотношением

( ) = ( ) − ( ⁄ ) = ( ) − ( ⁄ ) .

Если статистические связи между символами отсутствуют, энтропия сигнала на выходе линии связи равна H(Y). При наличии статистической связи энтропию определяют с использованием цепей Маркова.

Согласно формуле (3.16)

Соответственно скорость передачи информации по каналу с помехами определяется равенством

а пропускная способность дискретного канала с помехами определяется как предельное значение скорости передачи по каналу:

Здесь p(x) – множество распределений вероятностей входных сигналов, формируемых источником. Если техниче-

101

ская скорость Vt передачи элементов сообщений фиксирована, то пропускная способность может достигаться за счет изменения статистических свойств последовательностей символов посредством их преобразования (кодирования).

При наличии помех пропускная способность канала связи вычисляется как произведение количества принятых в секунду знаков n на разность энтропии источника сообщений и условной энтропии источника сообщений относительно принятого сигнала:

С = n [Н (X) — H(X/Y)] бит/сек,

В общем случае

= [ ( ) − ( ⁄ )] = [ ( ) − ( ⁄ )] = = [ ( ) + ( ) − ( )] бит/с.

Если символы источника сообщений неравновероятны и взаимозависимы, то энтропия источника считается по формуле общей условной энтропии. Действие помех в канале связи также может быть подсчитано по формуле условной энтропии. В этом случае в формулах условных энтропий будут участвовать разные условные вероятности. В первом случае это будут условные вероятности появления одного символа в зависимости от вероятности появления некоторого другого символа, а во втором случае это будут условные вероятности перехода одного символа в другой под действием помех в канале связи. Безусловные вероятности появления символов на выходе источника сообщений (или на входе приемника) должны быть заданы или определены по условию.

102

Для симметричных бинарных каналов, в которых сигналы передаются при помощи двух качественных признаков и вероятность ложного приема рл = р(1/0) = р(0/1), а вероятность правильного приема рп = 1—рл потери учитываются при помощи условной энтропии вида

На практике чаще всего приходится решать задачу определения пропускной способности при заданном проценте искажений в канале связи. В случае бинарных каналов задается вероятность или процентное соотношение перехода 1 в 0 и наоборот.

Для симметричных дискретных каналов связи с числом качественных признаков n > 2 пропускная способность

На практике предельные возможности канала обычно не достигаются. Степень загрузки канала характеризуется коэф-

фициентом использования:

= (̅) ,

где (̅) - производительность источника сообщений;

103

С - пропускная способность канала связи.

Поскольку нормальное функционирование канала возможно при изменении производительности источника в пределах 0 ≤ (̅) ≤ С, λ может изменяться 0 ≤ λ ≤ 1.

Теорема Шеннона для канала связи с шумом:

Существует способ кодирования, позволяющий обеспечить передачу сообщения с R < C по каналу с помехами со сколь угодно малой вероятностью ошибочного приема.

Если R > C, то существует способ кодирования, при котором потеря информации будет сколь угодно близко приближаться к нижней границе R – C, но никогда не сможет стать меньше R – C.

Теорему, доказанную Шенноном, обобщали последователи, снимая предположения о дискретности, локальной ограниченности мощности сигнала, о гауссовости сигналов и «белизне» помех и т. д. В настоящее время теорема стала фундаментальным фактом теории связи.

Теорема далеко не очевидна, можно сказать, парадоксальна, и с трудом усваивается в инженерной практике.

Во-первых, роль помех сказывается в том, что, если количество передаваемой информации превысит пропускную способность, помехи все равно уничтожат любой «избыток» информации и сведут темп ее передачи к непревосходимому уровню С.

Во-вторых, часто кажется, что помехи должны непременно искажать любое сообщение в той или иной степени независимо от того, как оно закодировано. Даже если передавать сообщения с большой избыточностью, все равно невозможно, как считают некоторые, добиться нулевой вероятности искажения. Ведь найдется такое длинное сообщение, где эта вероятность неизбежно проявится, какой-нибудь символ да исказится.

Однако, существуют «хитрые» способы кодирования, при которых искажения на выходе канала (в самом деле неизбежные, имеющие ненулевую вероятность!) удается скоррек-

104

тировать и восстановить правильно все символы без исключения. Иногда почему-то забывают, что помеховые искажения ‒ это не последние операции, которым подвергаются сообщения, что приемом искаженных помехами сообщений не заканчивается процесс передачи информации по каналу связи. Принятое сообщение никто не мешает подвергнуть на выходе дополнительной обработке. Именно она спасает положение ‒ искаженное сообщение удается восстановить, «очистить» от помех. Правда, восстановление может «дорого обойтись». Не исключено, что на него будет затрачено усилий больше, чем на передачу данных по каналу.

Теорема вдохновила и продолжает вдохновлять конструкторов аппаратуры на поиски «противопомеховых» способов кодирования. Пусть практическая их реализация часто сложна, громоздка, однако выгоды на выходе чаще всего превышают затраты на создание «антипомехового» оборудования.

5.5. Скорость передачи по непрерывному гауссову каналу связи

Под гауссовым каналом связи понимают математическую модель реального канала, удовлетворяющего следующим требованиям:

1)физические параметры канала известны и детермини-

рованы;

2)полоса пропускания канала ограничена полосой Fk

герц;

3)в канале действует аддитивный гауссов белый шум (с равномерным частотным спектром и нормальным распределением амплитуд);

4)статистическая связь между сигналом и шумом отсутствует, а ширина спектра сигнала и помехи ограничена полосой пропускания канала.

Длительность каждого одиночного сообщения равна Т

(рис. 5.4). Под состоянием, являющимся непрерывной функцией времени, можно понимать текущее значение сигнала или

105

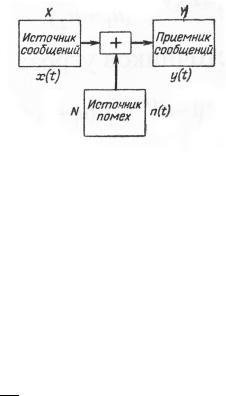
любой другой параметр. Для большей определенности под x(t) будем иметь в виду напряжение (ток). В дальнейшем полученные результаты легко обобщаются на большой класс других параметров сигналов (длительность, задержка, фаза, амплитуда и т. д.).

Рис. 5.4. Общая схема канала связи с помехами

В канале связи на передаваемое сообщение накладывается помеха n(t), являющаяся непрерывной функцией времени. В результате сложения x(t) и n(t) приемное устройство будет получать сообщение y(t), непрерывно изменяющееся во времени. Будем считать, что совокупности передаваемых сообщений x(t), помех n(t) и принимаемых сообщений имеют спектр, ограниченный полосой W.

Для таких сообщений можно определить, какое количество информации содержится в принятом сообщении относительно переданного, если воспользоваться теоремой Котельникова. Разобьем интервал времени Т на равные отрезки

величиной ∆ = , определяющие отсчетные точки на оси

времени. Отсчеты функций x(t), n(t) и y(t) в этих точках определяют сами непрерывные функции времени. Непрерывные сообщения можно заменить, таким образом, сообщениями с конечным числом элементов сообщений = 2 и с непрерывным распределением состояний. Таким образом, количество информации, содержащееся в принятых сообщениях Y относительно переданных X определяется равенством

106

Мы будем считать, что X и N статистически независимы, поэтому количество информации, которое содержится в Y, когда уже известно Н(Х), равное H(Y/X), обусловлено только шумами и равно H(N), т. е.

Тогда (5.5) можно представить в другой форме

Это количество информации измеряется в двоичных единицах, приходящихся на сообщение. Если ( , ) поделить на ремя Т, то определив количество информации, которое передается в среднем сообщениями Y о сообщениях X в единицу времени. Эта величина называется скоростью передачи информации по каналу связи с шумами и определяется равенством

→→

Устремление → ∞ означает, что для определения средней скорости передачи надо рассмотреть всю совокупность возможных сообщений.

Наибольшее значение скорости передачи информации называется пропускной способностью канала связи:

= макс = lim макс( ) (5.9)

→

Определим пропускную способность канала связи, когда помехи представлены в виде гауссовых шумов с нормальным законом распределения. Такие помехи обладают наибольшей эффективностью, поскольку энтропия сообщений максимальна, когда закон распределения нормальный при заданном уровне мощности.

Количество информации ( , ) можно определить через энтропию сообщений

107

Рис. 5.5. Непрерывные во времени сообщения в канале связи и их дискретные представления

Энтропия объединения шумов имеет максимальное значение, если все элементы шумов , ,…, распределены по нормальному закону и являются статистически независимыми. Так как элементы независимы, то энтропия объединения равна сумме энтропий

108

В этой форме 2 – число независимых элементов сообщения, ( ) – энтропия одного элемента (энтропия шума для одного отсчетного значения).

Для нормального закона распределения энтропия равна

где – дисперсия шума; ∆ – интервалы квантования.

Таким образом,

Если желательно передать наибольшее количество информации, то надо, чтобы энтропия объединения принятых сообщений (5.11) была максимальной. Для этого надо также выполнить два условия: во-первых, чтобы отсчеты принятого сигнала , ,…, были статистически независимыми, вовторых, чтобы отсчетные значения были распределены по нормальному закону.

В таком случае энтропия принятых сообщений равна

Из теории вероятностей известно, что если складываются две случайные величины, каждая из которых имеет нормальный закон распределения, то и суммарная случайная величина будет распределена по нормальному закону распределения. Следовательно, если и имеют нормальные законы распределения, то и имеет тот же закон. Статистическая независимость элементов сообщений n(t) и y(t) означает статистическую независимость элементов сообщений x(t).

Если совокупность сигналов с состояниями X обладает

дая из выборок для совокупности сообщений имеет нормальный закон распределения, то такие сигналы называются иде- ально-кодированными (по Шеннону).

Из изложенного следует, что максимальная энтропия (5.16), а значит, и скорость передачи сообщений возможны с применением шумоподобных сигналов.

Наибольшее количество информации, содержащееся в Y относительно X, в соответствии с (5.15) и (5.16) равно

макс( , ) = макс( ) − ( ) =

Если точность квантования передаваемых сообщений ∆ и принимаемых ∆ одинаковы, то наибольшее количество информации равно

Поэтому (2.126) можно преобразовать к виду

где Р – среднее значение мощности передаваемых сообщений;

110