
Колебания и волны. учеб.-метод. пособие. Москаленко А.Г., Татьянина Е.П
.pdf
КОЛЕБАНИЯ И ВОЛНЫ
Учебно-методическое пособие
A |
|
|
|
|
|
1 |
|
|
|
2 >β1 |
|
f0 |
|
3 |
>β2 |
|
|
|
|
2 |
|
|
|
0 |
|
|
|
0 |
рез |
|
|
|
0 |
|
|
Воронеж 2018
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Воронежский государственный технический университет»
КОЛЕБАНИЯ И ВОЛНЫ
Утверждено учебно-методическим советом университета в качестве учебного пособия
Воронеж 2018
УДК 531:530.145(075.8) ББК 22.317:22.314я7
К602
Авторы:
А. Г. Москаленко, Е. П. Татьянина, И. М. Трегубов, Т. Л. Тураева
Колебания и волны: учеб.-метод. пособие [Электронный ресурс]. – Электрон. текстовые и граф. данные (1 , 6 Мб) / А. Г. Москаленко, Е. П. Татьянина, И. М. Трегубов, Т. Л. Тураева - Воронеж: ФГБОУ ВО «Воронежский государственный технический университет», 2018. – 1 электрон. опт. диск (CD-ROM): цв. – Систем. требования: ПК 500 и выше; 256 Мб ОЗУ; Windows XP; SVGA с разрешением 1024x768; Adobe Acrobat; CD-ROM дисковод; мышь. – Загл. с экрана.
ISBN 978-5-7731-0670-8
Учебно-методическое пособие «Колебания и волны» по дисциплине «Физика» предназначено для студентов всех технических направлений очной и заочной форм обучения. В пособии содержатся основной теоретический материал, примеры решения задач, контрольные вопросы, задачи для самостоятельного решения и тесты.
Ил. 36. Библиогр.: 10 назв.
УДК 531:530.145(075.8) ББК 22.317:22.314я7
Рецензенты: кафедра общей физики Воронежского государственного университета (зав. кафедрой д-р физ.-мат. наук, проф. А. Ф. Клинских);
д-р техн. наук, проф. А. В. Строгонов
ISBN 978-5-7731-0670-8 © Москаленко А. Г., Татьянина Е. П., Трегубов И. М., Тураева Т. Л., 2018
©ФГБОУ ВО «Воронежский государственный технический университет», 2018
3
ВВЕДЕНИЕ
Раздел «Физика колебаний и волн» является значительным и по содержанию и по объему курса общей физики. Важность этого раздела состоит в том, что полученные здесь закономерности широко используются в других разделах курса, таких как оптика, физика твердого тела, квантовая физика. В квантовой физике, в частности, вводится такое понятие, как «волны вероятности».
Общность уравнений, описывающих колебания и волны различной физической природы, как механической, так и электромагнитной, позволяет их параллельное рассмотрение, что и осуществлено в данном учебно-методическом пособии. Изложение теоретического материала ведется достаточно кратко, в соответствии с программой бакалавриата для технических специальностей, обращая главное внимание на физический смысл основных понятий и уравнений. Главная цель настоящего пособия – оказание помощи студентам в их самостоятельной работе при освоении данного материала. Этому способствует, прежде всего, подробный разбор и анализ решения целого ряда задач по каждой теме, а также наличие контрольных вопросов и тестовых заданий для самопроверки изученного материала. Большой подбор задач, взятых из различных стандартных сборников, позволяет дифференцировать студентам домашние задания.
3
1.МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
1.1.Гармонические колебания. Дифференциальное уравнение гармонических колебаний
Колебаниями называют процессы, характеризующиеся повторяемостью во времени. Простейшими из них являются гармонические колебания, при которых колеблющиеся величины изменяются со временем по закону синуса или косинуса. Колебания будут гармоническими, если возвращающая сила пропорциональна смещению от положения равновесия и амплитуда колебаний мала. Колебания могут происходить только в системах с устойчивым положением равновесия.
Кинематическое уравнение гармонических колебаний имеет вид
х(t) Acos( 0t 0 ) , |
(1.1) |
где x – смещение системы от своего положения равновесия; A – амплитуда колебаний; 0t 0 – фаза колебаний;
0 – начальная фаза; 0 - собственная циклическая частота.
График гармонических колебаний представлен на рис.1.1.
x |
|
A |
|
0 |
t |
|
|
A |
|
|
T |
|
Рис. 1.1 |
Скорость и ускорение колеблющейся точки определяются через первую и вторую производную соответственно
4
(t) |
dх |
A |
sin( t |
) , |
(1.2) |
|
|
||||||
|
dt |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
a(t) |
d 2 х |
A 2 cos( t |
) . |
(1.3) |
||||
|
|
|||||||
|
dt2 |
0 |
0 |
0 |
|
|
||
Из уравнений (1.2) и (1.3) следует |
дифференциальное |
|||||||
уравнение гармонических колебаний |
|
|
|
|
||||
|
|
d 2 x |
2 x 0 |
, |
|
|
(1.4) |
|
|
|
dt2 |
|
|
||||
|
|
0 |
|
|
|
|
||
решением которого является уравнение (1.1).
1.2. Собственные гармонические колебания. Пружинный, физический и математический маятники
Идеализированные системы, в которых колебания возникают за счёт первоначально сообщённой энергии при последующем отсутствии внешних воздействий и описываются уравнением (1.4), называются гармоническими осцилляторами. Примерами гармонических осцилляторов являются пружинный, физический и математический маятники. Колебания, возникающие в таких системах при отсутствии сил трения, называются собственными гармоническими колебаниями.
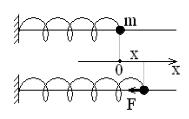
1.2.1. Пружинный маятник
|
Рассмотрим |
|
систему, |
|
|
состоящую |
из |
пружины с |
|
||
коэффициентом жесткости k, к |
|
||||
которой |
прикреплен |
шарик |
|
||
массой |
m, |
способный |
|
||
перемещаться вдоль |
гладкого |
|
|||
горизонтального |
|
стержня |
|
||
(рис.1.2). При смещении шарика |
|
||||
из |
положения |
равновесия |
Рис.1.2 |
||
возникает сила упругости Fx = -kx, |
|
||||
|
|
|
|
5 |
|

стремящаяся вернуть его в положение равновесия. Это возвращающая сила, она пропорциональна смещению и направлена всегда к положению равновесия.
Если трение в системе отсутствует, то по 2-му закону Ньютона:
m |
d 2 x |
kx или |
d 2 x |
|
k |
x 0 . |
(1.5) |
|
dt 2 |
dt 2 |
m |
||||||
|
|
|
|
|
Сопоставляя полученное дифференциальное уравнение с дифференциальным уравнением гармонического осциллятора (1.4) находим собственную циклическую частоту и период колебаний пружинного маятника
|
|
|
|
|
|
k |
|
|
, |
T |
2 |
2 |
|
k |
|
. |
|
|
(1.6) |
|
|
|
|
0 |
|
|
m |
|
|
0 |
m |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
1.2.2. Физический маятник |
|
|
|
|||||||||||||||
|
|
|
|
|
|
Физический маятник – твердое тело, |
||||||||||||||
|
|
|
|
способное совершать под действием силы |
||||||||||||||||
O |
|
|
|
тяжести |
колебания вокруг |
неподвижной |
||||||||||||||
|
|
|
точки, не совпадающей с |
его |
центром |
|||||||||||||||
|
c |
|
||||||||||||||||||
|
|
инерции |
(рис.1.3). |
В |
положении |
|||||||||||||||
|
|
|
|
равновесия центр инерции маятника С |
||||||||||||||||
|
|
C |
|
находится под точкой подвеса О, на одной |
||||||||||||||||
|
|
|
||||||||||||||||||
|
|
|
с ней вертикали. При отклонении маятника |
|||||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
от |
положения |
равновесия |
на |
угол |
|
|||||||||||
|
|
mg |
|
возникает вращательный момент |
|
|
||||||||||||||
|
|
|
|
|
|
|||||||||||||||
Рис.1.3 |
|
|
|
|
|
|
|
M mg c sin , |
|
|
||||||||||
|
|
|
|
стремящийся |
возвратить |
маятник |
в |
|||||||||||||
положение равновесия. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Обозначив момент инерции маятника относительно оси, |
|||||||||||||||||||
проходящей через |
точку |
подвеса |
|
буквой |
I, |
на основании |
||||||||||||||
основного закона динами при вращательном движении можно написать
6
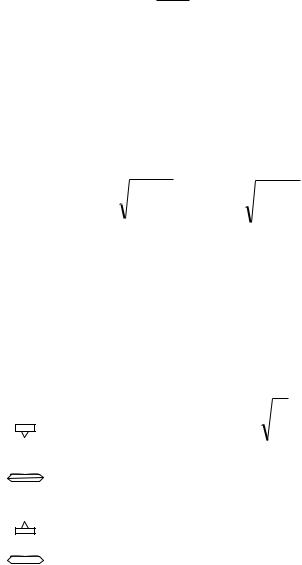
Id 2 mg c sin dt 2
В случае малых |
колебаний |
( 5 ) |
sin , |
|||||||
следовательно |
|
|
|
|
|
|
|
|
||
I |
d 2 |
mg |
|
|
или |
d 2 |
|
mg c |
0 . (1.7) |
|
|
c |
|
|
|||||||
|
dt 2 |
|
|
dt 2 |
|
I |
|
|||
|
|
|
|
|
|
|||||
Из сопоставления полученного уравнения с дифференциальным уравнением гармонического осциллятора (1.4), находим циклическую частоту и период колебаний физического маятника
|
|
|
mg c |
; |
T 2 |
|
I |
. |
(1.8) |
0 |
|
|
|
||||||
|
|
I |
|
|
mg c |
|
|||
|
|
|
|
|
|
||||
Таким образом, при |
малых |
колебаниях |
физический |
||||||
маятник совершает гармонические колебания с частотой o и периодом Т, описываемые уравнением
0 cos(0t 0 ) |
(1.9) |
||
Величина L |
I |
– называется приведенной длиной |
|
|
|||
m c |
|||
физического маятника. С учетом этого, период колебаний физического маятника определяется выражением
П1 |
|
|
|
|
|
|
|
|
T 2 |
L |
. |
(1.10) |
||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
g |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Физический |
маятник |
используется |
|||
|
|
|
|
|
|
|
|
|
Г1 |
|||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
для определения |
ускорения |
свободного |
|||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
падения. Наиболее точные измерения |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
П2 |
|
|
|
|
|
|
|
|
выполняются |
с |
помощью |
оборотного |
|||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
маятника, который позволяет исключить |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
Г2 |
момент инерции |
из |
расчетной формулы |
||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
(1.8). Физический оборотный маятник |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
представляет собой стержень, на котором |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Рис.1.4 |
укреплены две |
опорные призмы П и |
||||||||||||
7

подвижные грузы Г, позволяющие изменять период колебаний (рис.1.4). При совпадении периодов колебаний T1 T2 относительно призм П1 и П 2 , расстояние между призмами
определяет приведенную длину L , которую можно измерить с большой точностью.
1.2.3. Математический маятник
Математический маятник – идеализированная система, состоящая из материальной точки массой m, подвешенной на нерастяжимой невесомой нити длиной , и колеблющаяся под действием силы тяжести.
Математический маятник можно представить как частный случай физического маятника. Для математического
маятника момент инерции I m 2 . Подставив это выражение в формулы для циклической частоты и периода колебания физического маятника (1.8), получим известные выражения для малых колебаний математического маятника:
|
|
|
|
g |
|
; T 2 |
|
|
|
. |
(1.11) |
0 |
|
|
|
||||||||
|
|
|
|
g |
|
||||||
|
|
|
|
|
|||||||
Из сопоставлений формул (1.8) и (1.11) для периодов физического и математического маятников следует, что приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.
1.3. Сложение гармонических колебаний
Результирующее движение точки, одновременно участвующей в нескольких колебаниях, во многих случаях является колебательным. Таким образом, можно говорить о сложении нескольких колебаний в одно результирующее.
8
1.3.1. Сложение гармонических колебаний одного направления
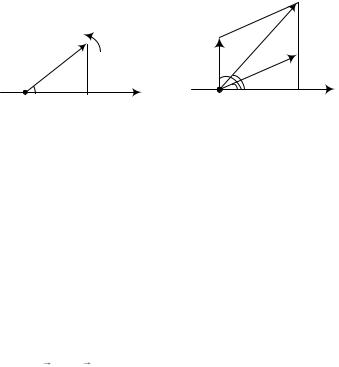
Это действие осуществляется с помощью вектора амплитуды, позволяющего свести сложение колебаний к сложению векторов. Вектор амплитуды представляет собой вектор, величина которого равна амплитуде гармонических колебаний, а угол между его направлением и осью Ox определяется начальной фазой (рис.1.5). Если привести
|
|
|
|
|
|
A |
|
A |
0 |
A2 |
2 |
|
|
|
|
|
A |
|||
|
0 |
|
|
|
1 |
1 |
|
x |
|
|
x |
||
0 |
x |
|
0 |
|
Рис.1.5 |
Рис.1.6 |
вектор во вращение против |
часовой стрелки с угловой |
скоростью 0, то его проекция на ось Ox будет изменяться со временем по гармоническому закону (1.1). Следовательно, гармоническое колебание может быть задано с помощью вращающегося вектора амплитуды.
Рассмотрим сложение двух гармонических колебаний одного направления и одинаковой частоты, описываемых уравнениями:
|
x1 A1 cos(0t 1) , |
(1.12) |
|
|
x2 A2 cos(0t 2 ) . |
(1.13) |
|
Представим |
эти колебания с |
помощью |
векторов |
|
|
|
|
амплитуды A1 и A2 |
и построим вектор |
A , представляющий |
|
результирующие колебания (рис.1.6).
Из построения найдём амплитуду и фазу результирующего колебания
9
