
Методическое пособие 529
.pdf
q 2 |
|
LI 2 |
|
qmax2 |
|
LImax2 |
const |
(4.7) |
|
2C |
2 |
2C |
2 |
||||||
|
|
|
|
|
4.2. Свободные затухающие колебания в колебательном контуре
Перейдем |
к |
|
|
рассмотрению |
|
|
|
I |
||||||||||||||
реального |
|
колебательного |
|
контура, |
|
|
|
|
|
|
||||||||||||
обладающего |
активным |
сопротивлением |
q |
|
|
|
|
|
||||||||||||||
(рис. 4.3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Закон |
|
Ома |
для RLC -контура при |
|
|
|
R |
|
||||||||||||||
|
|
|
|
|
||||||||||||||||||
разряде конденсатора на сопротивлении и |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
индуктивности запишется так |
|
|
|
|
|
|
|
|
Рис. 4.3 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
IR |
q |
L |
dI |
, |
|
|
|
(4.8) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
C |
|
dt |
|
|
|
|
|
|
|
|
|
|
|||
а после преобразования, примет вид |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
q |
R |
q |
1 |
|
q 0 . |
|
(4.9) |
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
L |
LC |
|
|
|
|
|
|
|
|
|
|
|||||
Введя обозначения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
R |
2 , |
1 |
|
|
2 , |
|
(4.10) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
L |
|
|
|
|
|
LC |
0 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
получим |
стандартное |
|
|
дифференциальное |
|
уравнение |
||||||||||||||||
затухающих электромагнитных колебаний (аналогичное уравнению (1.10))
|
|
|
|
|
|
q 2 q 2 q 0 . |
(4.11) |
||
|
|
|
|
|
|
|
|
0 |
|
Решение данного уравнения имеет вид |
|
||||||||
|
|
|
|
|
|
q q |
e t cos( t ) , |
(4.12) |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
где |
|
|
2 |
2 |
− частота |
затухающих |
колебаний, |
||
|
|
|
0 |
|
|
|
|
|
|
q |
max |
(t) q |
e t |
− |
амплитуда |
заряда, изменяющегося по |
|||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60 |
|
|
экспоненциальному закону, 2RL − коэффициент затухания
колебаний.
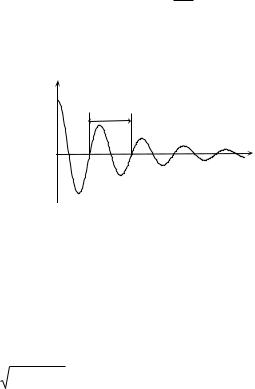
График функции (4.12) представлен на рис. 4.4.
q
T
0 |
t |
Рис. 4.4
Затухание электромагнитных колебаний, как и механических, принято характеризовать логарифмическим декрементом затухания
|
|
|
ln |
qmax (t) |
T , |
(4.13) |
|
|
|
qmax (t T ) |
|||
где T |
|
1 |
- период затухающих колебаний. |
|
||
|
|
|
||||
2 |
2 |
|
||||
|
|
|
|
|
||
0 |
|
|
|
|
|
|
Логарифмический декремент затухания (см. 1.28) обратен
числу колебаний N e , совершаемых за время, в |
течение |
||
которого амплитуда уменьшается в e раз: |
|
||
|
1 |
. |
(4.14) |
|
|||
|
Ne |
|
|
Наряду с логарифмическим декрементом затухания, колебательный контур характеризуют его добротностью
Q |
|
Ne . |
(4.15) |
|
|
||||
|
|
|
61
Добротность контура тем выше, чем больше число колебаний
N e , |
при |
котором амплитуда |
уменьшается |
в e раз. Через |
||||||||||||||
параметры контура добротность определяется выражением |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
1 |
|
|
|
L |
. |
|
|
(4.16) |
|||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
R |
|
|
|
C |
|
|
||||
|
Из |
формулы |
периода |
|
|
|
|
q |
|
|
|
|
||||||
затухающих колебаний следует, |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
что |
при |
2 |
2 |
T , |
т.е. |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
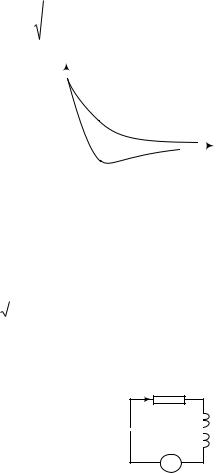
вместо колебаний происходит |
|
|
|
|
|
|
|
|
|
|
|
|||||||
апериодический |
|
разряд |
|
|
|
|
|
|
|
|
|
|
|
|||||
конденсатора (рис. 4.5). |
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Сопротивление |
контура, |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
при |
котором |
наблюдается |
|
|
|
|
|
|
|
|
|
Рис. 4.5 |
||||||
переход |
от |
колебательного |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
режима |
к |
апериодическому, |
|
|
|
|
|
|
|
|
|
|
|
|||||
называется |
|
критическим. |
|
|
|
|
|
|
|
|
|
|
|
|||||
Значение |
критического |
сопротивления |
определяется |
|||||||||||||||
выражением |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Rкр 2 L / C . |
(4.17) |
||||||||||||
4.3. Вынужденные электрические колебания
Вынужденные электрические колебания в RLC -контуре (рис. 4.6) возникают при наличии в нем переменной ЭДС, изменяющейся по гармоническому закону
E (t ) E |
0 |
cos |
t. |
(4.18) |
||
E |
E |
|
в |
|
||
Закон |
Ома для |
неоднородного |
||||
участка цепи |
1 R L 2 |
в данном |
||||
контуре имеет вид
I R
q
C 
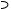 L
L
~
E (t)
Рис. 4.6
62

IR |
q |
L |
dI |
E |
cos |
t. |
(4.19) |
|
|
||||||
|
C |
|
dt |
E 0 |
в |
|
|
|
|
|
|
|
|
Проведя преобразования с использованием ранее принятых обозначений, получим дифференциальное уравнение вынужденных колебаний в контуре
q 2q 0 q |
|
E |
cosвt. |
(4.20) |
|||
E 0 |
|||||||
|
|
2 |
|
|
|||
|
|
|
|
|
|||
|
|
|
|
L |
|
|
|
Частное решение этого уравнения, описывающее установившиеся вынужденные гармонические колебания,
имеет по аналогии с механическими (1.33) , вид |
|
|
|
|
|
||||||||||||
|
|
|
|
q qmax cos(в t 0 ) , |
|
|
(4.21) |
||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qmax |
|
|
EE0 |
|
|
|
|
|
|
|
|
EE0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
L |
(02 в2 )2 4 2 в2 |
в |
|
R2 (в L 1/ вC)2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
||
|
|
|
tg 0 |
|
2в |
|
|
|
|
R |
|
. |
(4.22) |
||||
|
|
|
2 2 |
|
|
L 1/ |
|
||||||||||
|
|
|
|
|
|
|
C |
|
|
|
|||||||
|
|
|
|
|
0 |
|
в |
|
|
|
в |
в |
|
|
|
|
|
Продифференцировав выражение (4.21) по t , найдем силу тока в контуре при установившихся колебаниях
|
I |
dq |
q |
|
|
|
sin( |
t |
|
) I |
|
|
cos( |
t ) , (4.23) |
|||||||||||
|
|
max |
в |
0 |
max |
||||||||||||||||||||
|
|
|
dt |
|
|
|
|
|
|
|
в |
|
|
|
|
|
в |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где I |
max |
q |
max |
|
в |
− амплитуда силы тока, |
|
|
0 |
− сдвиг по |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
фазе между током и ЭДС. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Амплитуда силы тока I max |
и начальная фаза определяются |
||||||||||||||||||||||||
формулами |
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Imax |
|
|
|
|
E |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
R2 ( |
L 1/ |
C) |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
в |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
63 |
|
|
|
|
|
|
|
|
|

|
|
|
|
tg |
в L 1/ в C |
. |
|
|
|
|
|
|
|
(4.24) |
|||||||
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Резонансные |
|
|
кривые |
для |
|
|
I |
|
|
|
|
|
|
|
|||||||
силы тока при различных значениях |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
сопротивления R |
представлены на |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
рис. 4.7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R2 |
||
Амплитуда |
|
|
|
силы |
тока |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
(см. 4.24) максимальна при условии |
|
|
|
|
|
R1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в L |
|
|
0 . |
|
|
|
|
|
|
0 |
|
р 0 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
вС |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.7 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, |
резонансная |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
частота для силы тока совпадает с |
|
Uc |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
собственной частотой контура |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
рез 0 |
|
|
|
1 |
|
. |
(4.25) |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
LC |
|
|
min |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Резонансные |
|
|
кривые |
для |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
напряжения на конденсаторе |
U C |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
при различных R представлены на |
|
|
|
|
|
|
|
|
р 0 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
рис. 4.8. Точно такой же вид имеют |
|
|
|
|
|
|
|
|
Рис. 4.8 |
|
|
|
|||||||||
резонансные кривые и для заряда |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
q . Они сходны |
|
с резонансными кривыми для механических |
|||||||||||||||||||
колебаний (рис. 1.10). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Резонансная частота для напряжения |
U C и заряда q |
||||||||||||||||||||
определяется формулой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2 |
2 2 |
1 |
|
|
|
|
R2 |
|
. |
(4.26) |
|||||||
|
|
|
|
|
|
|
|
||||||||||||||
Uррез |
|
|
|
0 |
|
|
LC |
|
|
2L2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Максимум при резонансе получается тем выше и острее, чем меньше активное сопротивление и больше индуктивность контура.
64
4.4. Плоская электромагнитная волна. Скорость распространения и свойства электромагнитной волны
Существование электромагнитных волн непосредственно вытекает из системы уравнений Максвелла в
дифференциальной форме |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
D |
|
|
|
||||
, E |
; |
, H |
j |
; |
|
|||||
|
|
t |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|||
( , D) ; |
|
( , B) 0 ; |
|
|
|
(4.27) |
||||
и системы материальных уравнений |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
j E ; |
|
|
D |
0 E ; |
B |
0 |
H . |
(4.28) |
||
Применяя |
данную |
систему |
к |
|
однородной |
|||||
( const, const) , |
нейтральной |
( 0) , |
|
непроводящей |
||||||
( 0) среде |
получим |
волновые |
уравнения |
для |
плоской |
|||||
электромагнитной волны, распространяющейся вдоль оси Ox :
2 E |
y |
|
|
|
|
2 E |
y |
, |
(4.29) |
|
|
0 |
|
|
|||||
x2 |
0 |
|
|
t 2 |
|
|
|
||
|
|
|
|
|
|
|
|
||
2 H |
z |
|
|
|
|
2 H |
z |
. |
(4.30) |
|
|
0 |
|
|
|||||
x2 |
|
0 |
|
|
t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициент при второй производной по времени в волновом уравнении, есть величина, обратная фазовой скорости волны. Следовательно, уравнения (4.29) и (4.30) указывают на то, что скорость электромагнитной волны определяется выражением
|
1 |
|
|
. |
(4.31) |
|
|
|
|||
|
0 |
|
|||
|
0 |
|
|
|
В вакууме ( 1 , 1)
|
1 |
3 |
108 м/с, |
||
|
|
||||
|
0 0 |
||||
|
|
|
|||
65

скорость электромагнитных волн совпадает со скоростью света в пустоте c , поэтому фазовая скорость в среде
|
|
|
|
|
|
c |
|
|
|
|
|
|
||
|
|
|
|
|
|
. |
|
|
|
|
(4.32) |
|||
|
|
|
|
|
|
|
|
|
|
|||||
Решением волновых уравнений (4.29) и (4.30) являются |
||||||||||||||
функции, описывающие плоскую электромагнитную волну |
|
|||||||||||||
|
|
|
Ey Emax cos( t kx 1 ) , |
|
(4.33) |
|||||||||
|
|
|
H z |
H max cos(t kx 2 ) . |
|
(4.34) |
||||||||
В этих формулах - частота волны, k |
2 |
– волновое число, |
||||||||||||
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 = 2 |
|
|
|
|
|
|
|
|
|
|
|
|||
– |
начальные |
фазы |
колебаний |
векторов |
E |
и |
H . |
|||||||
|
|
|
|
|
|
|
|
|
|
|
y |
|
z , |
|
Векторы |
E и |
H |
направлены |
вдоль |
осей |
и |
||||||||
следовательно, |
|
взаимно |
перпендикулярны |
|
и |
|||||||||
перпендикулярны |
к направлению |
распространения |
волны, |
|||||||||||
образуя |
с |
вектором |
|
|
|
|
правовинтовую систему. |
|||||||
скорости |
||||||||||||||
Таким |
образом, |
|
электромагнитные |
волны |
поперечны. |
|||||||||
Колебания напряженностей электрического и магнитного поля в электромагнитной волне происходят синфазно ( 1 = 2 ) ,
одновременно достигая максимальных значений и обращаясь в нуль. Амплитуды этих векторов связаны соотношением
0 Emax  0 H max . (4.35)
0 H max . (4.35)
Пространственная структура плоской электромагнитной волны для фиксированного момента времени изображена на следующей диаграмме (рис. 4.9):
66

E y ( x, t ) |
|
|
|
0 |
|
x
Hz (x,t)
Рис. 4.9
4.5. Энергия электромагнитной волны
Электромагнитные волны переносят энергию. Плотность энергии электромагнитного поля слагается из плотности энергии электрического поля и плотности энергии магнитного поля:
|
|
|
E 2 |
|
H 2 |
|
|
w wE wH |
|
0 |
|
0 |
|
. |
(4.36) |
|
|
|
|||||
|
|
|
2 |
|
2 |
|
|
Поскольку колебания векторов |
E и H |
происходят с |
|||||
одинаковой фазой, то из условия (4.35), связывающего амплитудные значения этих векторов, следует аналогичное соотношение для их мгновенных значений
0 E 0 H . |
(4.37) |
С учетом (4.37) wE wH , получим |
|
w 0 0 EH . |
(4.38) |
Введем понятие плотности потока энергии, как энергии, переносимой электромагнитной волной в единицу времени через площадку единичной площади, ориентированной перпендикулярно скорости распространения волны. Модуль плотности потока энергии равен
67
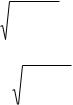
|
|
S w EH . |
(4.39) |
|
В векторной |
форме, |
с учетом соответствующих |
||
|
|
|
|
|
направлений векторов E, |
H и , будем иметь |
|
||
|
|
|
|
|
|
S |
E, H |
(4.40) |
|
это выражение получило |
название вектора |
Пойнтинга. |
||
Направление вектора |
|
совпадает с направлением переноса |
||
S |
||||
энергии, а его модуль равен плотности потока энергии
электромагнитной волны. |
|
|
|
|
|
|
||
|
Среднее значение модуля вектора Пойтинга за период |
|||||||
его |
полного |
колебания |
определяет |
интенсивность |
||||
электромагнитной волны |
|
|
|
|
|
|
||
|
|
I |
|
|
EH . |
(4.41) |
||
|
|
|
|
|||||
|
|
|
S |
|
||||
|
|
|
|
|
|
|
|
|
4.6. Эффект Доплера для электромагнитных волн
При движении источника и приемника электромагнитных волн друг относительно друга, как и в акустике, также наблюдается эффект Доплера. Соотношения, описывающие эффект Доплера для электромагнитных волн в вакууме, устанавливаются на основе специальной теории относительности. В случае сближения источника и приемника волн вдоль соединяющей их прямой регистрируемая частота определяется формулой
|
|
|
1 / c |
|
|
, |
0 |
|
0 |
||||
|
1 / c |
|
||||
|
|
|
|
|||
а в случае их взаимного удаления
|
|
|
1 / c |
|
|
. |
0 |
|
0 |
||||
|
1 / c |
|
||||
|
|
|
|
|||
68
В данных формулах c представляет собой относительную скорость движения источника и приемника электромагнитных волн.
4.7. Контрольные вопросы
1.Какой вид имеет дифференциальное уравнение собственных электромагнитных колебаний в LC контуре?
2.Какой вид имеет дифференциальное уравнение затухающих электромагнитных колебаний в RLC контуре и его решение?
3.Что понимается под временем релаксации и от чего оно зависит?
4.Какова зависимость логарифмического декремента от параметров контура?
5.Что характеризует добротность контура? От чего она
зависит?
6.При каком сопротивлении контура процесс становится апериодическим?
7.Каковы условия вынужденных электромагнитных колебаний в контуре? Запишите дифференциальное уравнение вынужденных электромагнитных колебаний и его решение для установившегося процесса.
8.В чем заключается и как объясняется явление резонанса? Каков вид резонансных кривых для напряжений и токов в контуре?
9.Каковы основные свойства электромагнитной волны? Представьте ее графическое изображение.
10.Запишите волновое уравнение и уравнение плоской электромагнитной волны.
69
