
Методическое пособие 529
.pdf
откуда
tg 0 |
0 |
1 |
и 0 |
arctg ( 1) |
|
. |
|||
0 x0 |
4 |
||||||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
A x2 |
|
2 |
=35 см. |
|
|
|||
|
0 |
|
|
||||||
|
|
0 |
|
2 |
|
|
|
||
|
|
|
|
|
0 |
|
|
|
|
С учетом численных значений уравнение колебаний и уравнение скорости частицы можно представить в виде
|
4t |
|
|
; |
x 35cos |
,см |
|
||
|
|
4 |
|
|
x140sin 4t см / с.
4
Вискомый момент времени t=2,4с координата х и скорость частицы будут иметь соответственно значения
х=-29см и = -80 см/с.
Задача 2. Точка совершает гармонические колебания вдоль некоторой прямой с периодом Т=0,6с и амплитудой А=10см. Найти среднюю скорость точки за время, в течение которого она проходит путь А/2: а) из положения равновесия; б) из крайнего положения.
Решение
Выберем за начало отсчета времени момент, когда точка проходит положение равновесия. Тогда уравнение колебаний будет иметь вид
x Asin 0t.
Исходя из этого уравнения определим момент времени t1, соответствующий положению точки х = А/2. Имеем
A2 Asin 2T t1 , откуда t1 12T .
Значение средней скорости точки при ее движении из положения равновесия определяется из формулы
20
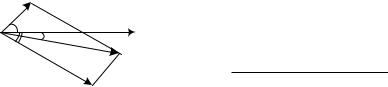
|
|
|
S |
|
|
A |
; |
|
|
|
100см / с. |
||||||||
ср1 |
|
|
|
ср1 |
|||||||||||||||
|
|
t |
|
|
2t1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Время движения точки из крайнего положения до |
|||||||||||||||||||
половины амплитуды будет равно t |
|
|
|
T |
t |
|
T |
. |
|||||||||||
2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
1 |
6 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
С учетом этого |
|
|
|
A |
; |
|
|
|
50см / с. |
||||||||||
ср 2 |
|
|
cр2 |
||||||||||||||||
|
|
|
|
|
2t2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Задача 3. Найти |
|
амплитуду и |
|
начальную фазу |
|||||||||||||||
результирующего колебания, возникающего при сложении двух одинаково направленных колебаний, выражаемых уравнениями:
x1 3cos t 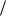 3 см, x2 8sin t
3 см, x2 8sin t 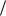 3 см.
3 см.
Написать уравнение результирующего колебания.
Решение
Вначале, используя тригонометрические формулы, приведем уравнение второго колебания к виду
x2 |
|
|
8cos t |
см. |
|
|
|
6 |
А1
1
О 2 |
|
x |
А
А2
Рис. 1.14
найдем: А=8,5 см. Тангенс начальной
определится из рис.1.14.
Затем, построим векторную диаграмму сложения однонаправленных колебаний (рис. 1.14). Согласно теореме косинусов получим
A 
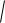 A12 A22 2A1 A2 cos ,
A12 A22 2A1 A2 cos ,
где 2 1.
Произведя вычисления,
фазы результирующего колебания
21

tg A1 sin 1 A2 sin 2 , A1 cos 1 A2 cos 2
=-0,2 рад.
Уравнение результирующего колебания запишете в
виде
x 8,5cos t 0,2 см.
Задача 4. Точка участвует в двух колебаниях с одинаковыми периодами и начальными фазами. Амплитуды колебаний А1=3см и А2=4см. Найти амплитуду результирующего колебания, если колебания взаимно перпендикулярны.
Решение
Если колебания взаимно перпендикулярны, то уравнение результирующего движения будет:
|
x2 |
|
y 2 |
|
2xy |
cos |
|
sin 2 |
|
|
|
. |
|
|
|
|
|
|
2 |
2 |
|||||||
|
A2 |
|
A2 |
|
A A |
|
1 |
|
|
1 |
|||
|
|
|
|
|
|
|
|
|
|
||||
1 |
2 |
|
1 |
2 |
|
|
|
|
|
|
|
||
Так как по условию |
начальные фазы |
складываемых |
|||||||||||
колебаний равны, то разность фаз ( 2– 1)=0, и, следовательно, cos0=1, sin0=0. С учетом этого уравнение результирующего колебания можно упростить
x2 |
|
y 2 |
|
2xy |
0 , или ( |
x |
|
y |
)2 0 , |
||
A2 |
A2 |
A A |
A |
A |
|||||||
|
|
|
|
|
|||||||
1 |
|
2 |
|
1 |
2 |
|
1 |
2 |
|
||
откуда
y A2 x . A1
Результирующим будет колебание точки вдоль прямой (рис. 1.15). Амплитуда этого колебания определится по теореме Пифагора

 12 22 5см .
12 22 5см .
y |
|
|
А2 |
А |
|
|
|
|
0 |
А1 |
x |
Рис. 1.15 |
|
|
22

1.7.2. |
Динамика гармонических колебаний |
Задача |
1. На концах тонкого стержня длиной =1м и |
массой m1=0,4кг укреплены шарики малых размеров массами m2=0,2кг и m3=0,3кг. Стержень колеблется около горизонтальной оси, перпендикулярной стержню и проходящей через его середину. Определить период колебаний, совершаемых стержнем.
|
|
|
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m2 |
||||||||
Стержень с шариком (рис. |
1.16) |
|
|
|
|
|
|
|||||||||||||||||||
представляет собой физический маятник, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
период колебаний |
которого |
|
определяется |
|
|
|
m1 |
|
|
|
|
|||||||||||||||
формулой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
T 2 |
|
|
I |
, |
|
|
|
|
|
|
|
|
O |
|
|
|
с |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
mg c |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где I – момент инерции маятника относительно |
|
|
C |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
оси колебаний; m – его масса; c – расстояние |
|
|
|
|
|
|
m3 |
|||||||||||||||||||
от центра масс маятника до оси. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Принимая |
|
|
|
|
|
шарики |
|
|
за |
Рис.1.16 |
||||||||||||||||
материальные точки, |
|
|
|
|
общий |
|
момент |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
инерции маятника определяем выражением |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
I |
1 |
m 2 m |
|
2 |
m |
|
2 |
|
1 |
2 m 3m 3m , |
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
12 |
l |
2 |
3 |
|
12 |
|
1 |
2 |
|
|
|
3 |
|
|
|
|||||||||||
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
I=158 кг м2. |
|
|
|
|
|
|
|||
Масса маятника |
m m1 m2 |
m3 |
0,9 |
кг. Расстояние |
|||||||||
c от оси маятника до его центра масс равно |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
mi xi |
|
m1 |
0 m2 |
|
|
m3 |
|
|
|
|
m3 m2 |
|
|
|
|
|
||||||||||
c |
|
|
|
2 |
|
|
2 |
|
|||||
mi |
|
m1 m2 m3 |
|
|
|
2m |
|||||||
|
|
|
|
|
|
|
|||||||
Произведя вычисления, найдем
c = 5,55 см, Т= 11,2 с.
23
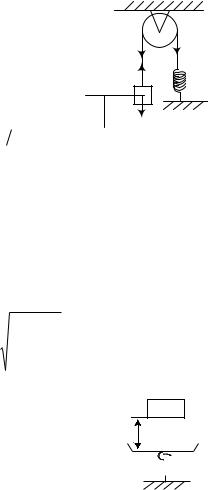
Задача 2. Найти частоту малых колебаний системы, показанной на рис.1.17. Известны радиус блока R, его момент инерции I относительно оси вращения, масса тела m и жесткость пружины k.
Решение
В состоянии равновесия mg kx0 ,
– деформация пружины. При отклонении тела на величину х движение данной системы описывается уравнениями:
mx mg T1 , I T1 T2 R .
Учитывая, что x R |
|
и |
||
T2 k x0 x mg kx , получим |
|
|
|
|
x |
k |
|
|
x 0 . |
|
|
|
||
m |
I |
|
||
R2 |
|
|
||
|
|
|
|
|
|
|
|
I |
T1 |
R |
|
|
|
|||
|
T2 |
||
|
|
||
|
|
|
|
|
|
|
O T1
x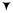
mg
РисРис. 1..17.6
Это равенство представляет собой дифференциальное уравнение, описывающее гармонические колебания данной системы. Сопоставляя его со стандартным видом дифференциального уравнения, найдем
0 |
k |
|
|
. |
|
|
|
||
m |
I |
|
||
|
|
|
||
|
R2 |
|
|
|
|
|
|
|
Задача 3. Тело массой m упало с высоты h на чашку пружинных весов (рис. 1.18). Массы чашки и пружины пренебрежимо малы, жесткость последней k. Прилипнув к чашке, тело начинает совершать гармонические колебания в вертикальном направлении. Найти амплитуду колебаний и их энергию.
m
h
 k
k
Рис..11.18.7
24

Решение
Учитывая то, что масса чашки мала, закон сохранения механической энергии запишется в виде
mgh |
kx2 |
mgx , |
|
||
2 |
|
|
где х – деформация пружины, после прилипания тела к чашке весов.
Приведя данное уравнение к стандартному виду, и решая его относительно х, найдем
xmax |
mg |
m2 g |
2 2kmgh |
. |
|
k |
|
||
|
|
|
|
В состоянии статического равновесия тела на весах выполняется условие
mg kx0 ,
откуда x0 mg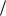 k .
k .
Таким образом, амплитуда колебаний груза на пружине определится как разность полученных значений, т.е.
A x |
|
x |
|
|
mg |
I |
2kh |
. |
max |
0 |
|
|
|||||
|
|
|
k |
|
mg |
|||
|
|
|
|
|
|
|||
Энергия колебаний найдется из формулы
E |
kA2 |
|
m2 g 2 |
mgh . |
|
|
|||
2 |
|
2k |
|
|
Задача 4. Частица массой m=0,01кг совершает гармонические колебания с периодом Т=2с. Полная энергия колеблющейся частицы E=0,1мДж. Определить амплитуду А колебаний и наибольшее значение силы Fmax, действующей на частицу.
Решение
Для определения амплитуды колебаний воспользуемся выражением полной энергии частицы:
25

E 12 m 2 A2 ,
где = 2/Т. Отсюда амплитуда
A |
T |
|
2E |
2 |
|
m |
|
|
|
Так как частица совершает гармонические колебания, то сила, действующая на нее, является квазиупругой и, следовательно, может быть выражена соотношением F=-kx, где k – коэффициент квазиупругой силы; х – смещение колеблющейся точки. Максимальной сила будет при максимальном смещении хmax равном амплитуде:
Fmax=kA.
Коэффициент k выразим через период колебаний: k m 2 m 4 2 / T 2 .
Подставив выражения для А и k в формулу для максимальной силы и произведя упрощения, получим
Fmax 2  2mE / T .
2mE / T .
Произведем вычисления:
А= 45мм, Fmax 4,4 мН.
1.7.3.Затухающие и вынужденные колебания
Задача 1. В воде плавает льдина в виде параллелепипеда с площадью основания S и высотой Н. Льдину погружают в воду с начальной скоростью 0 .
Определить ее скорость в произвольный момент времени, если сила сопротивления воды пропорциональна скорости льдины.
26

|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
|
|
|
|
До погружения льдина находится в равновесии. На нее |
|||||||||||||||||
действуют |
две |
|
|
силы (рис.1.19, |
а): |
|
сила |
тяжести |
||||||||||
mg лVg л SHg |
(где |
л – |
|
|
|
|
|
|
|
|
|
|||||||
плотность |
|
|
льда) |
|
и |
|
FА |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
F |
|
x |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
выталкивающая сила Архимеда |
|
|
|
|
|
|
|
|
||||||||||
Н |
|
|
h |
Н |
h |
|
|
|
||||||||||
FA В Shg (где в – плотность |
|
Fc |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
воды; h – глубина погружения |
|
mg |
|
|
|
|
x |
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
льдины |
|
в |
|
|
|
состоянии |
|
а) |
|
|
1. |
5 |
|
б) |
|
|||
равновесия). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Рис.1.19 |
|
|
|
||||||
|
При погружении льдины |
|
|
|
|
|
|
|
|
|
||||||||
на дополнительную глубину х (рис.1.19,б) появляются |
||||||||||||||||||
дополнительная сила Архимеда |
F В Sxg В Sgx |
и сила |
||||||||||||||||
сопротивления воды Fc |
r . Под действием этих сил льдина |
|||||||||||||||||
будет совершать затухающие колебания. Применяя второй |
||||||||||||||||||
закон Ньютона, получим дифференциальное уравнение этих |
||||||||||||||||||
колебаний |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
mx rx В Sgx |
|
|
|
|
|
|
|||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 x 2 x 0 , |
|
|
|
|
|
|
|
(1) |
|||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
где |
|
|
r |
|
|
|
– |
|
коэффициент |
|
|
затухания, |
а |
|||||
|
|
|
2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
В Sg |
|
|
|
В Sg |
|
В g |
– |
собственная |
|
частота |
||||||
|
m |
|
л SH |
л H |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
колебаний. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Как известно, решением уравнения (1) является |
|||||||||||||||||
функция |
|
|
|
|
|
|
|
|
sin t |
|
, |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x A e t |
0 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
где |
2 |
2 |
|
- частота затухающих колебаний. |
|
|
|
|||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
|
|
|
|
|
|
|
|
|

Скорость колебания льдины
x A0e t cos t 0 sin t 0 .
Начальную амплитуду А0 и начальную фазу 0 определим из начальных условий (при t=0, х=0, х'(0) = 0):
0 A0 sin 0 ,
0 A0 sin0 A0 cos0 .
Откуда 0 0 , A0 0 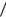 .
.
Таким образом, колебания льдины происходят по
закону
x 0 e t sin t .
Тогда искомая скорость льдины в произвольный момент времени
|
0 |
|
|
|
t |
. |
x |
cos t |
|
sin t e |
|
||
|
|
|
|
|
|
Задача 2. Тело массой m=5г совершает затухающие колебания. В течение времени t=50с тело потеряло 60 своей энергии. Определить коэффициент сопротивления r.
Решение
Энергия тела, совершающего гармонические колебания, определяется по формуле
|
|
E |
mA2 2 |
. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
2 |
|
|
|
Учитывая |
зависимость |
амплитуды |
затухающих |
||||
колебаний от времени |
|
|
|
|
|
|
|
|
|
A= A e t , |
|
|
|||
|
|
0 |
|
|
|
|
|
получим |
|
|
|
|
|
|
|
E |
mA2e 2 t 2 |
|
|
|
|
e 2 t , |
|
0 |
или |
E= E |
(1) |
||||
|
|||||||
|
2 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
28

|
|
|
mA2 2 |
|
|
|
|
|
|
|
где |
E0 |
0 |
– энергия тела в момент времени t=0. |
|||||||
2 |
||||||||||
|
|
|
|
|
|
|
|
|
||
|
|
К моменту времени t=50с тело потеряло 60% своей |
||||||||
первоначальной энергии, следовательно, |
|
|||||||||
|
|
|
|
E 0,4E0 . |
(2) |
|||||
|
|
Приравнивая (1) и (2), сокращая на Е0 |
и логарифмируя |
|||||||
обе части равенства, найдем: |
|
|||||||||
|
|
|
|
ln 2,5 2 t . |
|
|||||
|
|
Отсюда выражаем : |
|
|||||||
|
|
|
|
|
ln 2,5 |
. |
(3) |
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
2t |
|
|||
|
|
С другой стороны, |
|
|||||||
|
|
|
|
|
r |
. |
(4) |
|||
|
|
|
|
|
||||||
2m
Из сравнения (3) и (4) получим
r m ln 2,5 . t
После подстановки числовых значений найдем r = 9,16 10-5 кг/с.
Задача 3. Тело массой m=10г совершает затухающие колебания с максимальным значением амплитуды 7см, начальной фазой, равной нулю, коэффициентом затухания, равным 1,6с-1. На это тело начала действовать внешняя периодическая сила, под действием которой установились вынужденные колебания. Уравнение вынужденных колебаний имеет вид x 5sin 10t 0,75 см. Найти: 1) уравнение
свободных колебаний; 2) уравнение внешней периодической силы.
29
