Методическое пособие 521

10. Решить задачу одномерной теплопроводности

где

а) k=1, Q=1 при 0 x 1/2 и Q=0 при 1/2 x 1;

б) Q=1, k=1 при 0 x 1/2 и k=3 при 1/2 x 1.

11.С помощью МКЭ найти решение краевой задачи из упр. 4 или 5 разд. 4 «Метод Ритца», дискретизируя уравнения методом Галеркина. Показать сходимость.

Указание. Весовые функции {Wi} взять теми же, что и аппроксимирующие функции {Ni}, т.е. с малым носителем. При этом максимальный порядок производных от {Ni} под интегралом следует понизить методом интегрирования по частям.

12.Решить задачу из упражнения 4, б раздела 8, используя конечные элементы с иерархическими базисными функциями.

Указание. Рассмотрим последовательность конечноэлементных аппроксимаций

e 1e N1e e2 N2e ,

e 1e N1e e2 N2e e3N3e ,

e 1e N1e e2 N2e e3N3e e4 N4e и т.д.,

где

N1e ( 1)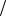2, N2e (1 )2

– обычные функции формы лагранжевого элемента 1-го порядка,

150

– при p 3 так называемые иерархические базисные функции. Приведенные аппроксимации справедливы для стандартного конечного элемента: –1 1. Нетрудно видеть, что первые два параметры 1e и e2 здесь совпадают со значениями функ-

ции e в точках =–1 и =1 соответственно, а всем остальным параметрам придать подобный смысл не так просто. Да в этом и нет особой необходимости, так как слагаемые e3N3e , e4 N4e , …

играют роль поправок к линейной аппроксимации. Тем не менее, можно записать

т.е. равны производной (p–1)-го порядка от e в середине конечного элемента. Проверьте, что приведенные функции формы обеспечивают непрерывность решения на границах элементов.

Каждая следующая функция Nep имеет степень много-

члена на единицу больше, чем предыдущая. Предположим, получено решение задачи (1) для обычных линейных конечных элементов. Добавляя к аппроксимации на каждом конечном элементе слагаемое e3N3e , получим новое решение (2),

более точное чем (1), поскольку оно основано уже на квадратичной аппроксимации. Точно так же, используя еще одно дополнительное слагаемое e4 N4e , найдем решение (3) – приближение кубическим полиномом. И так далее. Подумайте, в чем преимущество такого подхода?

И в заключение отметим, что переход от произвольного элемента x [x1, x2] к стандартному [–1, 1] можно осуществить по формуле

x x2 x1 x1 x2 . 2 2

При этом требуется всего лишь совершить замену переменной в интегралах, вычисляемых по области конечного элемента.

151

13. Указанная в предыдущем упражнении система иерархических функций отнюдь не единственно возможная. Приведем еще одну систему, определяемую интегрированием от полиномов Лежандра:

N3e 2 1, N4e 2( 3 ),

Производные этих функций обладают ортогональностью

– свойством, весьма полезным при вычислениях. Решите одну из задач упражнения 4 раздела 4, используя последовательно указанные иерархические функции. Выведите явно матрицу S системы уравнений. Сделайте вывод.

14. Для нелинейного дифференциального уравнения

с краевыми условиями (0) = 0, (1) = 1 провести дискрети-

зацию и получить численное решение на основе МКЭ

15. Края x=0 и x=1 плиты с коэффициентом теплопроводности k=1 поддерживаются при температуре 10 и 80 C. Найти стационарное распределение температуры , если тепло генерируется внутри плиты со скоростью a 2 (a=0,01 0,03) на единицу длины.

152

7. РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ

7.1. Введение

Интегральным называется уравнение, в котором неизвестная функция y(x) входит под знаком интеграла:

b(x)

F(y(x),x) (x,s,y(s))ds.

a(x)

Уравнения вида

b(x)

называются линейными. В этих уравнениях функция двух переменных K(x,s) называется ядром интегрального уравнения, функция f(x) – свободным членом. Число в уравнении (7.1) выступает как параметр. Если f(x) 0, то уравнение (7.1) называется однородным, в противном случае – неоднородным.

В частном случае, когда a(x)=const a, b(x)=x, (7.1) на-

зывается уравнением Вольтерра 2-го рода:

x

a

а уравнение (7.2) – уравнением Вольтерра 1-го рода:

x

K(x,s)y(s)ds f (x).

a

Если в (7.1) и (7.2) за оба предела интегрирования взять фиксированные числа, т.е. a(x)=const a, b(x)=const b, то придем к уравнению Фредгольма 2-го рода

b

y(x) f (x) K(x,s)y(s)ds

a

153

и уравнению Фредгольма 1-го рода –

b

K(x,s)y(s)ds f (x).

a

При этом функции f(x) и K(x,s) предполагаются квадратично суммируемыми соответственно на основном промежутке [a, b] и в основном квадрате = [a, b] [a, b], т. е. выполняются условия

b b

dt | K(t,s) |2 ds ,

a a

b

| f (t) |2 dt .

a

Решением интегрального уравнения на отрезке [a, b] называется всякая функция y= (x), которая будучи подставленной в это уравнение, обращает его в тождество относительно всех x [a, b].

7.2. Метод последовательных приближений

Методом последовательных приближений, или итерационным методом, можно решать линейные интегральные уравнения Вольтерра и Фредгольма 2-го рода. Метод состоит в построении последовательности функций y0(x), y1(x), y2(x), …, yn(x), … Если удается сделать предельный переход при n ,

то получим точное решение y*(x) y(x) , в противном

n

случае решение будет получаться приближенным при условии, что метод сходится. Для определенности рассмотрим уравнение Вольтерра 2-го рода

x

y(x) f (x) K(x,s)y(s)ds .

a

В качестве нулевого приближения y0(x) обычно полагают y0(x)=f(x). Первое приближение вычисляется подстановкой y0(x) вместо y(x) в правой части исходного уравнения (7.1) –

154

x

y1(x) f (x) K(x,s)y0(s)ds,

a

второе приближение – подстановкой y1(x) и т.д.

x

y2(x) f (x) K(x,s)y1(s)ds ,

a

x

y3(x) f(x) K(x,s)y2(s)ds,

a

. . . . . . . . . . . . . . . . .

x

yn(x) f (x) K(x,s)yn 1(s)ds.

a

Если два соседних приближения yn(x) и yn–1(x) мало отличаются друг от друга, то yn(x) принимают за приближенное решение данного уравнения. Критерием близости двух функций может служить, например, L2 - норма их разности:

Итерационный процесс можно записать в операторной

форме. Пусть Kˆ – оператор умножения y(x) на K(x,s) и интегрирования по отрезку [a, b] или [a, x]

k 1

Если этот ряд сходится, то он сходится независимо от начального приближения.

155

Такой подход позволяет получить решение через так называемую резольвенту. Действительно,

x x

Ky0(x) K(x,s)y0(s)ds K1(x,s)y0(s)ds K1y0(x)

a

где

x

Kj(x,s) K(x,t)Kj 1(t,s)dt.

t

Резольвентой ядра K(x,s) называется сумма ряда

R(x,s, ) j 1Kj(x,s),

j 1

который при любых фиксированных значениях сходится равномерно относительно x [a, b] и s [0, x] при условии, что ядро K(x,s) непрерывно. Таким образом, выражение (7.4) переходит в формулу

x

y*(x) f (x) R(x,s, )y0(s)ds.

a

156

Для уравнений Вольтерра метод последовательных приближений сходится всегда. Для уравнений Фредгольма итерационный процесс сходится, если ядро K(x,s) ограничено в ос-

A(b a)

K(x,s).

Пример. Методом последовательных приближений решить уравнение Фредгольма 2-го рода

1

y(x) x 2 (xt t)y(t)dt .

0

Решение.

Берем начальное приближение

y0(x) f (x) x.

Первое и последующие приближения:

Начиная с четвертого приближения решение уже не меняется. Следовательно, итерационный процесс сошёлся за конечное число итераций, и получено точное решение:

y(x) 121x 40 . 81 81

157

Этот результат в системе Maple можно получить, используя команды:

>restart; a:=0;b:=1;

>f:=x->x;K:=(x,t)->(-t+x*t);lambda:=2;

>F:=z->f(x)+lambda*int(K(x,t)*z(t),t=a..b);

>y1:=unapply(F(f),x);

>y2:=unapply(F(y1),x);

>y3:=unapply(collect(F(y2),x),x);

>y4:=unapply(collect(F(y3),x),x);

>y5:=unapply(collect(F(y3),x),x);

7.3. Операционный метод

Если в интегральном уравнении Вольтерра 2-го рода ядро K(x,s) зависит лишь от разности аргументов, а нижний предел интегрирования равен нулю, то такое уравнение называется типа свертки по Лапласу:

x

Для решения уравнений такого вида используется преобразование Лапласа. Пусть функции f(x), K(x,s) – оригиналы. Можно показать, что решение в этом случае также будет оригиналом. Полагая

применим к обеим частям уравнения (7.5) преобразование Лапласа. Учитывая, что согласно известной теореме изображение свертки двух функций есть произведение их изображений, получим

Y(p) F(p) K(p)Y(p),

158

Оригинал для Y(p) будет решением интегрального уравнения.

Отметим, что к уравнению типа свертки по Фурье

y(x) f (x) K(x s)y(s)ds

может быть применен аналогичный метод, основанный на преобразовании Фурье.

7.4.Численные методы решения интегральных уравнений

7.4.1.Метод конечных сумм

Пусть задано интегральное уравнение Фредгольма 2-го

рода

b

с параметром, не равному собственному числу соответствующего однородного уравнения. Основная идея метода конечных сумм основана на приближенном вычислении интеграла с помощью некоторой квадратурной формулы. Пусть известно, что

где Ak и xk – весовые коэффициенты и узлы квадратурной формулы, Rn – остаток квадратуры.

Если правило (7.7) применить к вычислению интеграла в (6), то получим

где k – веса, а sk – узлы формулы (7).

Пример. Решить уравнение

2

y(x) (x t)y(t)dt x3.

0

159