Файловый архив студентов. Файловый архив студентов.
1260 вузов, 4603 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Воронежский государственный технический университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Методическое пособие 476

.pdf
Скачиваний:
2
Добавлен:
30.04.2022
Размер:
1.76 Mб
Скачать
☆

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Воронежский государственный технический университет

В.В. Горбунов О.А. Соколова

НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА

ЧАСТЬ 3

Утверждено Редакционно-издательским советом университета в качестве учебного пособия

Воронеж 2004

1

УДК 517.2

Горбунов В.В., Соколова О.А. Начала математического анализа. Ч. 3: Учеб. пособие. Воронеж: Воронеж. гос. техн.

ун-т, 2004. 82 с.

В учебном пособии излагаются элементы теории дифференциальных уравнений и рядов. Теоретический материал иллюстрируется большим количеством примеров. Содержатся вопросы для самопроверки и задачи для самостоятельного решения.

Учебное пособие соответствует требованиям Государственного образовательного стандарта высшего профессионального образования по направлению 6151000«Конструкторскотехнологическое обеспечение автоматизированных машиностроительных производств», специальности 151002 «Металлобрабабативающие станки и комплексы», дисциплине «Математика».

Учебное пособие подготовлено на магнитном носителе в текстовом редакторе Microsoft Word и содержится в файле

“МатАн3.doc”.

Ил. 1. Библиогр.: 6 назв.

Научный редактор д-р физ.-мат.наук, проф. В.Д. Репников

Рецензенты: кафедра естественно-научных дисциплин Международного института компьютерных технологий (зав. кафедрой канд. техн. наук, доц. С.П.Попов); д-р физ.-мат.наук, проф. В.А. Родин

Гобунов В.В., Соколова О.А., 2004 Оформление. Воронежский государственный технический университет, 2004

2

ВВЕДЕНИЕ

Современное машиностроительное производство предполагает наличие высокоразвитой системы технологического обеспечения. Компьютеризация конструкторско-технологической подготовки требует наличие хорошей математической подготовки.

Данное пособие продолжает серию пособий по высшей математике и посвящено изучению следующих разделов: дифференциальные уравнения, числовые ряды и степенные ряды.

Пособие имеет следующую структуру. В начале каждого параграфа приводятся соответствующие теоретические сведения (определения основных понятий, уравнения, формулы, правила, признаки, методы). Затем следуют вопросы для самопроверки и примеры решения типовых задач различной степени трудности. Далее предлагаются задачи для самостоятельного решения. Ко всем задачам даны ответы.

Учебное пособие соответствует требованиям Государственного образовательного стандарта высшего профессионального образования по направлению 657800 «Конструкторско-технологическое обеспечение машиностроительных производств», специальности 120200 «Металлобрабабативающие станки и комплексы».

3

1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

1.1. Основные понятия.

Часто при рассмотрении различных прикладных задач построение математических моделей приводит к уравнениям, связы-

вающим независимую переменную x , искомую функцию y y x

и производные функции различных порядков. Такие уравнения называются дифференциальными. Решением или интегралом диф-

ференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество. Так, решением уравне-

ния y

f x является функция

y

F x

- первообразная для

функции f(x).

 

 

 

Если неизвестная функция

y

y x

зависит от одной пе-

ременной, то дифференциальное уравнение называется обыкновенным. Дифференциальные уравнения в частных производных, соответствующие случаю зависимости искомой функции от нескольких переменных, в данном курсе не рассматриваются. Далее будем рассматривать только обыкновенные дифференциальные уравнения.

Наивысший порядок производной, входящей в дифференциальное уравнение, называется порядком этого уравнения.

Например, уравнение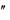 y 3y 2y 0 является обыкновенным дифференциальным уравнением второго порядка, а уравнение y 5xy y 2 - первого порядка.

Нахождение решения дифференциального уравнения называется его интегрированием, а график решения дифференциального уравнения представляется интегральной кривой.

1.2 Дифференциальные уравнения первого порядка. Основные понятия

Дифференциальное уравнение первого порядка, связывающее независимую переменную х, искомую функцию y x и ее производную у' в общем случае можно записать в виде

F x; y; y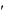 0 .

4

Дифференциальное уравнение первого порядка, разрешенное относительно у' , записывается в виде y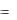f x; y .

Дифференциальное уравнение первого порядка может быть записано в дифференциальной форме

P x; y dx Q x; y dy 0 ,

где P x; yи Q x; y- известные функции.

Существует бесчисленное множество решений дифференциального уравнения, отличающихся друг от друга на постоянную величи-

ну. Легко догадаться, что решением уравнения y

2x является

функция y x2 , а также y

x2

1 или y x2

c , где с - const.

Бесчисленное множество решений дифференциального уравне-

ния первого порядка составляет понятие общего

решения дифферен-

циального уравнения .

 

 

 

 

Общим решением дифференциального уравнения

первого по-

рядка называется функция

y

x;c , содержащая одну произволь-

ную постоянную c , обращающая для любого фиксированного значения c дифференциальное уравнение в тождество, причем, любое частное решение из вышеупомянутой совокупности решений может быть получено из общего решения при некотором конкретном значении c .

Частным решением дифференциального уравнения первого

порядка называется любая функция y

x;c , полученная из обще-

го решения y

x;c при конкретном значении постоянной c c0 .

Часто общее решение дифференциального уравнения может быть

получено только в неявном виде, т. е. в виде уравнения Ф x; y;c 0 ,

которое называется частным интегралом дифференциального уравнения.

С геометрической точки зрения общее решение y

x;c

пред-

ставляет собой семейство интегральных кривых на плоскости

Oxy .

Частное решение y

x; c0 соответствует одной кривая из этого

семейства. Для выделения конкретной кривой используется точка

x0 ; y0

, принадлежащая кривой. В этом случае говорят о начальном

условии

y0

x0 , которому удовлетворяет данное частное реше-

ние. Задача отыскания частного решения дифференциального урав-

5

нения первого порядка, удовлетворяющего заданному начальному условию, называется задачей Коши.

Теорема. Если в уравнении y

f x, y

функция f x, y и ее

частная производная

f

по у непрерывны в некоторой области D на

 

 

y

 

 

 

плоскости Оху, содержащей некоторую точку

x0 , y0

, то существу-

ет единственное решение этого уравнения

y

x , удовлетво-

ряющее условию y

y0 при x x0

(без доказательства).

Геометрический смысл теоремы заключается в том, что существует и притом единственная интегральная кривая, проходящая

через точку x0 , y0 .

1.3. Уравнения с разделяющимися переменными

Наиболее простым дифференциальным уравнением первого порядка является, уравнение вида

P x dx Q y dy 0 ,

где каждая из функций P x и Q y зависит только от одной пере-

менной. Такие дифференциальные уравнения называют уравнениями с разделенными переменными. Проинтегрировав почленно это уравне-

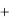ние, получаем: P xdx Q y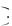dy c - его общий интеграл.

Дифференциальные уравнения с разделяющимися переменными имеют вид

P x Q y dx P x Q y dy 0 .

1

1

2

2

Уравнение легко сводится к предыдущему уравнению путем почленного деления его на Q1 y P2 x , после чего может быть получен общий интеграл:

 

P1

x

Q2

y

P1

x

 

Q2

y

 

 

 

 

 

dx

 

 

dy 0 ,

 

 

dx

 

 

 

 

dy c .

 

P2

x

Q1

y

P2

x

 

Q1

y

 

При проведении почленного деления дифференциального урав-

нения на Q1 y P2

x могут быть потеряны некоторые решения. По-

этому следует отдельно решить уравнение

Q1 y P2

x 0 и найти

6

особые решения дифференциального уравнения, которые не принадлежат семейству общего решения.

Пример. 1. Найти общее решение дифференциального урав-

нения

 

dy

 

 

 

y

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dx

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Решение: Разделим переменные

dy

 

dx

. Интегрируя, нахо-

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

x

 

 

 

 

 

 

 

дим

 

 

 

 

dy

 

 

 

 

 

dx

C,

т.е.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ln

y

 

 

 

 

ln

x

 

ln

C

 

или

 

ln

y

 

ln

C / x

; отсюда получаем общее

решение: у = С/x.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Пример 2. Найти общий интеграл дифференциального урав-

нения

 

y

xy dx

 

 

x xy dy

0 .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Решение:

 

 

 

Преобразуем

 

 

левую

 

 

часть

уравнения:

y 1

 

 

x dx

 

x 1

 

y dy

0. Делим обе части уравнения на xy

0 :

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

x

dx

1

y

dy

0.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Решением его является общий интеграл x

ln

x

 

ln

y

 

y

c , т.е.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ln

 

xy

 

 

x

y

c .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Здесь уравнение Q1 y P2 x

 

 

0 имеет вид

xy

0. Его реше-

ния

x

0 ,

y

0 являются решениями данного дифференциального

уравнения,

но

не

 

входят

в

общий

интеграл.

Значит,

решения

x

0, y

 

0 являются особыми.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Уравнение

y

 

f1 x f2 y

также сводится к уравнению с раз-

деленными переменными. Для этого достаточно положить

y

 

dy

и

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dx

разделить переменные.

7

1.4. Однородные уравнения первого порядка

Функция f x, y называется однородной функцией n-го по-

рядка относительно переменных х и у, если при любом

справедли-

во тождество

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

f

x,

y

n f

x, y .

 

 

 

 

 

 

 

 

Например,

функция

f

x; y

 

 

x2

2xy

есть

однородная

функция второго порядка, так как

 

 

 

 

 

 

 

 

 

 

 

 

f x, y

 

 

x 2

2 x y

2 x2

2xy

2 f x, y .

 

 

 

Дифференциальное уравнение

y

f

x; y

называется одно-

родным,

если функция

f

x; y

есть однородная функция нулевого

порядка.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Покажем, что однородное дифференциальное уравнение сво-

дится к уравнению с разделяющимися переменными. Если f x; y

-

однородная

функция

нулевого порядка,

то,

по определению,

f

x; y

0 f

x; y

f

 

x;

 

y .

Положив

 

1

,

получим

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

f

x, y

f

1,

y

 

, т.е. однородная функция нулевого порядка зави-

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

сит только от отношения

 

y

.

 

Поэтому сделаем подстановку v

 

y

,

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

x

т.е. y vx . Дифференцирование последнего равенства дает

 

 

 

 

 

 

 

 

 

 

 

dy

 

v

dv

x .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dx

 

 

dx

 

 

 

 

 

 

 

 

 

Подставляя производную в уравнение, получим дифференциальное уравнение с разделяющимися переменными

v

dv

x f (1, v) ,

dv

x f (1, v) v,

 

 

dv

 

dx

.

 

 

 

 

 

 

 

dx

dx

 

f (1, v) v

 

x

Интегрируя, находим

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dv

dx

C.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

f 1, v v

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

8

Возвращаясь после интегрирования к исходной функции y vx ,

получим интеграл уравнения.

Однородное дифференциальное уравнение часто задается в

дифференциальной форме:

P x; y dx Q x; y dy 0 . В этом случае

функции P x; y и Q x; y

должны быть однородными функциями

одинакового порядка. Дифференциальное уравнение переписывает-

ся в виде

dy

 

P x; y

,

где правая часть является однородной

 

 

 

dx

Q x; y

 

 

 

 

функцией нулевого порядка однородности.

 

 

Пример.

3

Найти

общий

интеграл

уравнения

x2 y2 dx

2xydy

0 .

 

 

 

 

 

Решение: Данное уравнение является однородным, т.к. функ-

ции P x; y

x2

y2

и Q x; y

2xy - однородные функции вто-

рого порядка.

 

 

 

 

 

 

 

 

Положим y

vx . Тогда

dy xdv

vdx . Подставляем в ис-

ходное уравнение:

 

 

 

 

 

 

 

 

 

x2

v2 x2 dx

2xvx xdv

vdx 0 ,

 

 

 

x2 1 v2

2v2 dx 2vx3du 0 ,

 

1 v2 dx 2vxdv 0.

Разделяем переменные

dx

 

2v

 

dv

 

0 и интегрируем

x

1 v2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ln

x

ln 1 v2 c, ln

x

1 v2

 

c,

x

 

1 v2

ec .

 

 

Обозначим c

c , c

0. Тогда

 

x

 

1 v2

c .

 

 

 

 

1

1

 

 

 

 

 

 

 

 

1

Заменяя v на

y

, получаем:

x2

y 2

c x - общий интеграл исход-

 

 

 

 

x

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ного уравнения.

9

1.5. Линейные дифференциальные уравнения первого порядка

Линейное дифференциальное уравнение первого порядка назы-

вается линейное относительно неизвестной функции и ее производной уравнение, имеющее вид

dy

dx

P(x) y Q(x) ,

где P( x) и Q( x) - заданные непрерывные функции или постоянные.

Рассмотрим метод Бернулли интегрирования данного уравнения. Решение линейного дифференциального уравнения ищется в виде

произведения двух неизвестных функций

y

 

u x v x

от x . Тогда

 

y

u v

uv . Подставляя выражение y

и

y

в уравнение, получа-

ем:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

u v

 

uv

P x uv

Q x

или u v

u v

 

P x v

Q x .

Подберем функцию v

v x

так, чтобы выражение в скобках было

равно

нулю,

 

т.е.

 

решим

дифференциальное

уравнение

v

P x v

 

0 .

 

Разделяем

переменные

 

интегрирования

 

dv

 

P x dx , интегрируя, получаем:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

v

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ln

v

 

 

P x dx

ln

c

.

 

 

 

 

 

Из

множества

функций

v x ,

обращающих

выражение

v

P x v в ноль, можно выбрать самую простую функцию, поло-

жив c

1, поэтому v

e

P x dx .

 

 

 

 

 

 

 

 

 

Подставляя найденную функцию v

в исходное уравнение, по-

лучаем u e

P x dx

Q x .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Решаем полученное уравнение с разделяющимися перемен-

ными:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

du

e

P x dx

Q x , du Q x e

P x dx dx ,

 

 

 

 

 

 

dx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

u

 

Q x e P x dx dx

c .

 

10

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности