Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Методическое пособие 476

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

1.76 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

Теорема Вейерштрасса. Если функциональный ряд					un x
					n 1
мажорируется числовым рядом		an , то он сходится равномерно,
	n 1
т.е. для любого >0 найдется такой номер				N , что для всех n > N
		Sn x		для всех x
будет выполняться неравенство	S	Sn x	<	для всех x	из облас-

ти D .

Следует отметить, что равномерно сходящийся функциональный ряд не обязательно мажорируем.

2.12. Свойства равномерно сходящихся функциональных рядов

Если функциональный ряд un x состоит из непрерывных

n 1

функций и равномерно сходится, то сумма ряда является тоже непрерывной функцией.

Если функциональный ряд un x состоит из непрерывных

n 1

функций и равномерно сходится, то интеграл от суммы ряда S x

представляется следующим образом:

b	b	b	b
S x dx	un x dx	u1 x dx	u2 x dx ... .
a	n 1 a	a	a

Если функциональный ряд	un x сходится равномерно, а
	n 1

члены ряда имеют непрерывные производные, то равномерно сходится и ряд, полученный почленным дифференцированием исходного ряда:

u1 x

x ...

x ,

n 1

причем S

x .

n 1

Пример. 14. Вычислить сумму ряда 1

3x2 4x3 ... .

Решение: Воспользуемся суммой геометрической прогрессии,

сходящейся при

<1,

1 x

x3 ...

Данный функциональный ряд является равномерно сходя-

щимся при

<1,

поскольку мажорируем сходящимся числовым

рядом 1

... , где

< q <1. Почленно продифференци-

ровав предыдущее равенство, имеем:

3x 2

4x3 ...

2.13. Степенные ряды

Самыми простыми и широко используемыми среди функциональных рядов являются степенные ряды

a xn	a	a x	a x2	... a xn	... ,
n	0	1	2	n

n 0

где действительные числа a0 , a1, a2 ,..., an ,... называются коэффици-

ентами ряда .

Рассматривают также степенной ряд, расположенный по сте-

пеням x x0 , т. е. ряд вида

a x	x n	a	a x	x	... a x	x n	... ,
n	0	0	1	0	n	0

n 0

где x0 - некоторое постоянное число. Однако он с помощью замены

x x	0	z	легко приводится к виду	a	n	x n .
	0				n
			n	0

2.14. Сходимость степенных рядов. Теорема Абеля.

Выясним вопрос о сходимости степенного ряда

an x n .

Теорема Абеля. Если степенной ряд

an x n

сходится при

x x0 0 , то он абсолютно сходится при всех значениях

x , удов-

x n

летворяющих неравенству

. Если же степенной ряд

n 0

расходится при x x0 0 , то он буден расходиться и при всех

x ,

удовлетворяющих неравенству

Доказательство. Так как по условию ряд

сходится, то

n 0

по необходимому признаку сходимости

lim a

0 . Поэтому ве-

личина a xn ограничена, т. е. найдется такое число M

0 , что для

n 0

всех n выполняется неравенство

a xn

M ,

0,1,2,... Для всех

x , удовлетворяющих неравенству

, величина g

1 и,

следовательно,

an x n

an x0n

x n

g n ,

0,1,2,... ,

x0n

т. е. модуль каждого члена ряда не превосходит соответствующего

члена сходящегося

ряда геометрической прогрессии. Поэто-

му по признаку сравнения при

ряд

xn абсолютно схо-

n 0

дящийся.

Если ряд

расходится при

, то он расходится и

n 0

при всех x , удовлетворяющих неравенству

Это легко показать методом доказательства от противного.

Если

допустить

сходимость

ряда

точке

x2 , для которой

, то по теореме

Абеля ряд

сходится

при всех x , удовле-

творяющих неравенству

, и,

в частности,

в точке x1 , что

невозможно.

2.15. Интервал и радиус сходимости степенного ряда.

Из теоремы Абеля следует, что должна найтись точка x0 0 ,

разделяющая множества точек сходимости и расходимости степен-

ного ряда. Интервал

;

и называют интервалом сходимости

степенного ряда.

Число R

называют радиусом сходимости

степенного

ряда.

Интервал

сходимости можно записать в виде

R ряд расходится.

R; R . При

Если ряд

сходится при всех значениях x

R , то счи-

таем, что R

. На концах интервала сходимости при x

R и при

R сходимость ряда проверяется в каждом случае отдельно.

Для нахождения радиуса сходимости степенного ряда

n 0

составим

ряд

из

модулей

членов

данного

степенного

ряда

a x

a x2

...

a xn

...

и применим к нему признак Да-

ламбера:

lim

un 1

lim

an 1 x n 1

lim

an 1

0 ,

0 .

an x

lim

an 1

По признаку Даламбера ряд сходится, если

т.е. ряд сходится при значениях x , удовлетворяющих неравенству

lim

an 1

lim

Для ряда

радиус абсолютной сходимости находится с

n 0

помощью формулы Коши-Адамара:

R lim	an		.
R lim	an	1	.
n	an	1
n

Аналогично, воспользовавшись радикальным признаком Ко-

ши, можно установить, что R . lim n an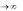

Если степенной ряд содержит не все степени x , т. е. задан неполный степенной ряд, то интервал сходимости ряда находят непосредственно применяя признак Даламбера или Коши.

		2n x n
Пример 15. Найти область сходимости ряда			.

n	0	n!

Решение: Воспользуемся формулой (17.1):

R lim

lim

n 1 !

lim n 1

2n 1

2 n

n 1!

Данный ряд абсолютно сходится на всей числовой оси.

x n

Пример 16. Найти область сходимости ряда n 1 2n .

Решение: Находим радиус сходимости ряда по формуле КошиАдамара:

R lim	2n 1	2 .
R lim	2n	2 .
n	2n
Следовательно, ряд сходится при		2	x 2 .
При x 2 имеем расходящийся ряд			1 n . При x 2
			n 1

имеем расходящийся ряд 1+1+1+1+…. Областью сходимости исход-

ного ряда является интервал 2,2 .

Пример 17. Найти область сходимости ряда

	x3		x3		x7			n 1	x2n 1
x						...	1			...
x						...	1			...
	3	5		7					2n 1

Решение: Заданный ряд неполный. Воспользуемся признаком Даламбера. Для данного ряда имеем:

						un		x2n	1		,					un 1				x2n 1				,


							2n		1										2n			1
			lim	un 1		lim		x2n 1				2n 1					x	2			lim		2n		1	x	2	.




				un				2n		1			x		2n 1								2n		1

			n			n															n
			n			n															n


		Ряд абсолютно сходится,												если x2							1 или				1 x			1.	При
x		1 имеем ряд 1					1		1					1		... , который сходится по призна-

							3		5					7
							3		5					7
ку	Лейбница.				При x				1						имеем			тоже						сходящийся					ряд
1	1		1	1	.... Следовательно, областью сходимости исходно-

	3		5	7
	3		5	7

го ряда является отрезок 1;1 .

2.16. Разложение функций в степенной ряд. Ряды Тейлора и

Маклорена

Для любой функции f

, определенной в окрестности точки

и имеющей в ней производные до

1 -го порядка включи-

тельно, справедлива формула Тейлора:

...

f n

...

Rn x ,

где

n 1

, c

x , x

остаточный

член в

1 !

форме Лагранжа.

Если функция

x бесконечно дифференцируема в окрест-

ности точки

x0 , а остаточный член

стремится к нулю при

т.е.

lim Rn

0 , то из формулы Тейлора получается раз-

ложение функции

f x

по степеням

называемое рядом

Тейлора:

n x0

x0 ...

Если в ряде Тейлора положить x0

0 , то получим разложение

функции по степеням x в ряд Маклорена:

x 2

...

f n 0

x n .

Ряд Тейлора можно формально построить для любой беско-

нечно дифференцируемой функции в окрестности точки x0 ,

но этот

ряд может не сходиться к порождающей функции

x .

Теорема 1. Для того чтобы ряд Тейлора функции

схо-

дился к

f x

в точке

x , необходимо и достаточно,

чтобы в этой

точке остаточный член

формулы Тейло-

1 !

ра стремился к нулю при n

, т. е. чтобы lim Rn

0 .

Доказательство. Пусть ряд Тейлора сходится к функции

в некоторой окрестности точки x0 ,

т. е.

f x

lim Sn

. Восполь-

зовавшись совпадением n -частичной суммы ряда

с много-

членом Тейлора Pn

x , находим:

lim Rn

lim f

lim Sn x

0 .

Обратно, пусть lim Rn x

0 . Тогда

lim Sn x

lim Pn x

lim f

R x

f x

lim Rn x

x .

На практике часто пользуются теоремой, которая дает простое

достаточное условие разложимости функции в ряд Тейлора.

Теорема 2. Если модули всех производных функции f

ог-

раничены в окрестности точки x0

одним и тем же числом M

0 , то

для любого x из этой окрестности ряд Тейлора функции f xсхо-

дится к функции f x .

2.17. Разложение некоторых элементарных функций в ряд Тейлора (Маклорена)

1. Разложим функцию f x ex в ряд. Найдем производные

функции, а также их значения в точке x

0 :

ex ,

x ex ,..., f

ex ,...,

1, f

1, ..., f

n 0

1,....

Воспользовавшись формулой Маклорена, имеем:

e x

...

... .

По формуле Коши-Адамара находим радиус сходимости сте-

пенного ряда: R

lim

1 !

lim n 1

, т.е. ряд

сходится в интервале

;

. Для всех

R; R

справедливо

неравенство

f n

e x

M , позволяющее утверждать, что

все производные в этом интервале ограничены одним и тем же чис-

лом M eR . Следовательно, lim R x 0						, а функция	y e x
			n	n
			n
представляется рядом
e x			x	x2
	1				... ,
	1	1!		2!	... ,
		1!		2!

сходящимся к производящей функции на всей действительной оси.

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20221.7 Mб22Методическое пособие 471.pdf
#
30.04.20221.7 Mб2Методическое пособие 472.pdf
#
30.04.20221.7 Mб3Методическое пособие 473.pdf
#
30.04.20221.72 Mб4Методическое пособие 474.pdf
#
30.04.20221.76 Mб2Методическое пособие 475.pdf
#
30.04.20221.76 Mб2Методическое пособие 476.pdf
#
30.04.20221.76 Mб3Методическое пособие 477.pdf
#
30.04.20221.76 Mб5Методическое пособие 478.pdf
#
30.04.20221.77 Mб5Методическое пособие 479.pdf
#
30.04.2022186.88 Кб3Методическое пособие 48.doc
#
30.04.2022308.47 Кб3Методическое пособие 48.pdf