Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Методическое пособие 476

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

1.76 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 95 6 7 8 9 > Следующая >>>

2.3. Необходимый признак сходимости числового ряда.

Нахождение n -й частичной суммы Sn и ее предела не удобно для практического использования. Поэтому для выяснения сходимости ряда устанавливают необходимые и достаточные признаки сходимости. Рассмотрим необходимый признак сходимости.

Теорема . Если числовой ряд

сходится, то его общий

n 1

член un

стремится к нулю, т.е. limun

0 .

Доказательство.

Пусть

числовой

ряд

сходится и

n 1

lim Sn

S . Тогда и lim Sn 1

S (при n

и ( n

). По-

скольку

при

получаем:

lim un

lim Sn

lim Sn 1

0 .

Следует отметить, что невыполнение необходимого условия

сходимости числового ряда означает его расходимость.

Пример 1. Исследовать сходимость ряда

n 1 n

Решение: Ряд

расходится, т.к.

n 1

lim un

lim

0 ,

т.е. выполняется достаточное условие расходимости ряда. Пример 2. Исследовать сходимость ряда

				1	1		1 2		1	n
		1				1		... 1		...
		1		1		1	2	... 1	n	...
				1			2		n
Решение:					Данный			ряд		расходится,	т.к.
limun	lim 1		1 n			0 .
limun	lim 1		n			0 .
n	n		n
n	n
Необходимый признак сходимости числового ряда не является
достаточным: из условия						limun		0 не следует что, ряд сходится.
						n

Существует множество расходящихся числовых рядов, для которых

limun 0 . Например, рассмотрим гармонический ряд

1		1	1	1	1	...	1	... .

n 1 n			2	3	4		n

Очевидно, что limun				0 . Однако гармонический ряд расхо-
	n

дится, что можно будет легко показать в дальнейшем с помощью интегрального признака сходимости Коши.

2.4. Теоремы сравнения

Сходимость и расходимость числовых рядов с положительными членами можно установить с помощью достаточных признаков сходимости, а также теорем сравнения.

Сходимость или расходимость знакоположительного ряда можно установить с помощью сравнения его с другим («эталонным») рядом, о котором заранее известно, сходится он или расходится. Такое сравнение производится на основе двух теорем сравнения.

Теорема 1. Пусть даны два знакоположительных ряда

un и

vn . Если для всех n выполняется неравенство un

vn , то из схо-

n 1

димости ряда

vn следует сходимость ряда

un ,

из расходимо-

n 1

сти ряда

следует расходимость ряда

vn .

n 1

Доказательство.

Обозначим

n -e

частичные

суммы

рядов

соответственно через S u

и S v

. Суммируя нера-

n 1

венства u

получаем, что S u

S v .

Пусть ряд

сходится и

lim S v

Члены ряда

n 1

положительны,

поэтому

Snv

S2 .

Используя

неравенство

Snu

Snv

получаем

Snu

S2 .

Последовательность

S u

, S u ,

S u , ... монотонно возрастает, поскольку u

>0, и ограни-

чена сверху числом S

, следовательно,

имеет предел

lim S n

S ,

т. е. ряд

сходится.

Пусть теперь знакоположительный числовой ряд

рас-

ходится: lim Snu

. Тогда, с учетом неравенства Snu

Snv

полу-

чаем

lim S v

, т. е. ряд

расходится.

Теорема 1 имеет место и в том случае, когда неравенство

выполняется не для всех членов рядов

vn ,

n 1

начиная с некоторого номера.

Теорема 2. Пусть даны два знакоположительных ряда

. Если существует конечный, предел lim

n 1

то ряды

un и

vn сходятся или расходятся одновременно (без

n 1

доказательства).

Пример 3. Исследовать на сходимость ряд	1		.
	n 1
		1 2n

Решение: Сравним данный ряд с рядом геометрической про-

грессии n 1 2n , о котором заранее известно, что он сходится. По-

скольку для любого n выполняется неравенство	1	1		, то из
	2n		2n
1

сходимости геометрической прогрессии следует и сходимость ряда

1		. Следовательно, данный ряд сходится.
n 1
n 1	1 2n
	Пример 4. Исследовать сходимость ряда							1		.



						n 1	3 n		1
						n 1
									2
									2
	Решение: Здесь un			1		. В качестве	эталонного ряда


			3 n		1
					1

					2
					2

сравнения возьмем расходящийся гармонический ряд с общим чле-

ном v

Имеем

. Следовательно,

исходный ряд

расходится.

Пример 5. Исследовать сходимость ряда

n 1

Решение: Для использования второй теоремы сравнения рас-

смотрим

lim

2 .

Поскольку данный предел оказался равен

отличной от нуля константе, то исходный ряд и ряд сравнения

1	1	1	1	1	...	1	... ведут себя одинаково в отношении

n 1 n		2	3	4		n

расходимости или сходимости. В данном случае оба числовых ряда расходятся.

2.5. Признак Даламбера

Признак Даламбера не требует для установления сходимости или расходимости числовых рядов с положительными членами привлечения других, известных рядов для сравнения. Для анализа сходимости числового ряда нужно производить некоторые операции над самим рядом.

Теорема 1.(Признак Даламбера). Если для числового ряда с

положительными членами

существует конечный или беско-

нечный придел lim

l ,

то ряд сходится при l

1 и расходится

при l

1. В случае l

1 признак не способен различить сходящийся

или расходящийся числовой ряд.

Доказательство.

По

определению предела

lim

un 1

для

любого

0 найдется натуральное число

N такое,

что при n

выполняется неравенство

или

Рассмотрим случай l

1. Можно подобрать

так, что число

1. Обозначим l

g ,

g 1. Тогда из правой части нера-

венства

un 1

получаем

g ,

или un 1

при n > N . Считая, что un 1

un ,

и придавая номеру n различ-

ные значения, получим серию неравенств:

uN 1	g uN ,
uN 2	g uN 1	g 2 uN ,
uN 3	g uN 2	g 3 uN ,
.......... .......... .......... .........,
uN k	g uN k 1	g k uN ,
.......... .......... .......... .......... ,

т.е. члены ряда uN	uN 1	uN 2	...	uN k	... меньше соответ-
ствующих членов ряда
guN	g 2uN	g 3uN	...	g k uN	...,

который сходится как ряд геометрической прогрессии со знаменате-

лем 0	g 1. Но тогда на основании признака сравнения сходится
ряд uN	uN 1 uN 2 ... uN k ... , являющийся остатком исход-

ного числового ряда. Следовательно, на основании первой теоремы о свойствах числовых рядов сходится и исходный ряд.

		Рассмотрим случай l		1. В этом случае lim	un 1	l 1 , по-
		Рассмотрим случай l		1. В этом случае lim		l 1 , по-
				n	un
				n
этому, начиная с некоторого номера N , выполняется неравенство
	un 1	1 , или un 1	un , т.е. члены ряда возрастают с увеличением
	un	1 , или un 1	un , т.е. члены ряда возрастают с увеличением
	un
номера n . Поэтому limun				0 . Поскольку не выполняется необхо-
			n

димое условие сходимости, то числовой ряд обязательно расходится.

Признак Даламбера целесообразно применять, когда общий член ряда как функция целочисленного аргумента содержит выра-

жение вида n! или an , т.е. убывает быстрее степенной функции.

		2n
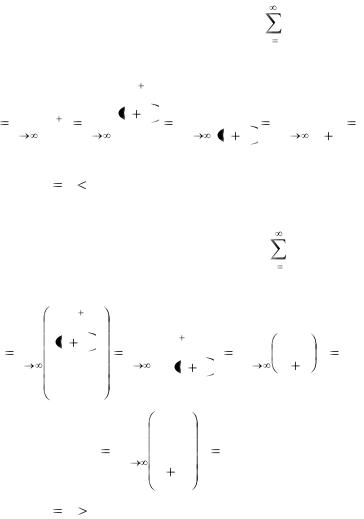
Пример 6. Исследовать на сходимости ряд			.
	n 1	n!

Решение: Находим

2n 1

lim

un 1

lim

n 1 !

2 lim

0 .

n 1 !

Так как l

1, то данный ряд по признаку Даламбера схо-

дится.

Пример 7. Исследовать на сходимость ряда

n 1

n 2

Решение: Вычисляем

2n 1

2n 1 n2

lim

2 lim

n 1

2 lim

2 .

Так как l

1, то данный ряд по признаку Даламбера рас-

ходится.

2.6. Радикальный признак Коши

Если в формуле общего члена числового ряда с положительными членами содержится n -ная степень какого-либо выражения, то удобно пользоваться радикальным признаком Коши.

Теорема (Радикальный признак Коши). Если для числового

ряда с положительными членами			un существует конечный или
			n 1

бесконечный придел lim n u	n	l ,	то ряд сходится при l 1 и рас-
n	n
n
ходится при l 1. В случае l		1 признак не способен различить

сходящийся или расходящийся числовой ряд.

Доказательство теоремы аналогично доказательству признака Даламбера

	n	n2
Пример 8. Исследовать на сходимость ряд	n	.

	n 1
n 1	n 1
Решение: Применим радикальный признак	Коши к ряду

n n2

n 1 n 1

Вычислим

l lim n u

lim n

lim

n 1

По радикальному признаку Коши исходный ряд сходится.

2.7. Интегральный признак Коши сходимости числового ряда с положительными членами

Теорема Если члены числового ряда с положительными чле-

нами un могут быт представлены как значения монотонно убы-

n 1

вающей	на промежутке 1,		функции	f x	так, что u1 f 1 ,
u2 f 2 , u3		f 3 и т.д., то числовой ряд			un и несобственный
				n	1
интеграл	f	x dx одновременно либо сходятся, либо расходятся.
	1
Несобственный интеграл			f x dx	геометрически соответст-
			1

вует площади криволинейной трапеции, ограниченной сверху гра-

фиком функции y 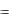f x , правая сторона которой удалена на бес-

конечность (Рис 1).

	u1
		u2			y=f(x)





			un 1	un
O					x
O	1 2 3		n-1	n	x
	1 2 3		n-1	n

Рис 1.

Построим прямоугольники на отрезке 1, n , суммарная пло-

щадь которых с недостатком и с избытком соответствует площади криволинейной трапеции. Основаниями прямоугольников являются отрезки 1,2 , 2,3 , 3,4и т.д.. Площадь прямоугольников с избыт-

<<< < Предыдущая 1 2 3 45 / 95 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20221.7 Mб22Методическое пособие 471.pdf
#
30.04.20221.7 Mб2Методическое пособие 472.pdf
#
30.04.20221.7 Mб3Методическое пособие 473.pdf
#
30.04.20221.72 Mб4Методическое пособие 474.pdf
#
30.04.20221.76 Mб2Методическое пособие 475.pdf
#
30.04.20221.76 Mб2Методическое пособие 476.pdf
#
30.04.20221.76 Mб3Методическое пособие 477.pdf
#
30.04.20221.76 Mб5Методическое пособие 478.pdf
#
30.04.20221.77 Mб5Методическое пособие 479.pdf
#
30.04.2022186.88 Кб3Методическое пособие 48.doc
#
30.04.2022308.47 Кб3Методическое пособие 48.pdf