Методическое пособие 334

3.Какими основными способами может атаковать криптоаналитик?

4.Что называется криптостойкостью алгоритма шифрования?

5.Какими основными величинами характеризуется сложность криптоаналитических атак?

6.Приведите примеры симметричных и асимметричных систем защиты информации.

19

Практическое занятие № 6 Модулярная арифметика

Модулярная арифметика часто изучается в школе как «арифметика часов» [3,11-13]. Если отсчитать 14 часов от 3 часов после полудня, то получится 5 часов утра следующего дня:

3+14 5 (mod 12)

или

(3+14) mod 12=5

Это арифметика по модулю 12.

Обычная запись в модулярной арифметике

a b(mod n)

читается так: «а сравнимо с b по модулю n». Это соотношение справедливо для целых значений a, b и n≠0, если, и только если

а = b + k * n

для некоторого целого к.

Отсюда, в частности, следует

n | (а - b).

Это читается как «n делит (а - b)».

Если a b(mod n), то b называют вычетом числа а по модулю n.

Операцию нахождения вычета числа а по модулю n

a(mod n)

называют приведением числа а по модулю n или приведением по модулю.

20

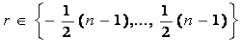
В нашем примере

(3 +14) mod 12 = 17 mod 12 = 5

или

17 5(mod 12),

число 5 является вычетом числа 17 по модулю 12.

Набор целых чисел от 0 до (n-1) называют полным набором вычетов по модулю n. Это означает, что для любого целого a(а>0) его вычет r по модулю n есть некоторое целое число в интервале от 0 до (n-1), определяемое из соотношения

r=а-к*n,

где к - целое число.

Например, для n=12 полный набор вычетов:

{0, 1, 2, …, 11}.

Обычно предпочитают использовать вычеты

rє{0,1,2, ... , n-1},

но иногда полезны вычеты в диапазоне целых:

Заметим, что

-12(mod 7) -5(mod 7) 2(mod 7) 9(mod 7) и т.д.

Модулярная арифметика аналогична во многом обычной арифметике: она коммутативна, ассоциативна и дистрибутивна. Точнее говоря, целые числа по модулю n с использованием операций сложения и умножения образуют коммутативное кольцо при соблюдении законов ассоциативности, коммутативности и дистрибутивности.

21

Фактически мы можем либо сначала приводить по модулю n, a затем выполнять операции, либо сначала выполнять операции, а затем приводить по модулю n, поскольку приведение по модулю n является гомоморфным отображением из кольца целых в кольцо целых по модулю n:

(а + b) mod n = [a(mod n) + b(mod n)] mod n, (а - b) mod n = [a(mod n) - b(mod n)] mod n. (а * b) mod n = [a(mod n) * b(mod n)] mod n,

[а * (b + с)] mod n = {[а * b(mod n)] + [а * c(mod n)]} mod n.

Криптография использует множество вычислений по модулю n, потому что задачи типа вычисления дискретных логарифмов и квадратных корней очень трудны. Кроме того, с вычислениями по модулю удобнее работать, потому что они ограничивают диапазон всех промежуточных величин и результата.

Для модуля n длиной к бит промежуточные результаты любого сложения, вычитания или умножения будут не длиннее 2к бит. Поэтому возведение в степень в модулярной арифметике можно выполнить без генерации очень больших промежуточных результатов.

Вычисление степени числа а по модулю n можно выполнить как ряд умножений и делений. Существуют способы сделать это быстрее. Поскольку эти операции дистрибутивны, быстрее произвести возведение в степень как ряд последовательных умножений, выполняя каждый раз приведение по модулю. Это особенно заметно, если работать с длинными числами (200 бит и более).

Например, если нужно вычислить

a8mod n,

не следует применять примитивный подход с выполнением семи перемножений и одного приведения по модулю громадного числа:

22

(а*а*а*а*а*а*а*а) mod n.

Вместо этого выполняют три малых умножения и три малых приведения по модулю:

((a2 mod n)2 mod n)2 mod n.

Тем же способом вычисляют

a16 mod n = (((a2 mod n)2 mod n)2 mod n)2 mod n.

Вычисление

ax mod n,

где х не является степенью 2, лишь немного сложнее. Двоичная запись числа х позволяет представить число х

как сумму степеней 2:

x = 25(10)-> 11001(2) , поэтому 25 = 24 + 23 + 20.

Тогда

a25 mod n = (а * a24) mod n = (а * а8 * a16) mod n =

= а * ((а2)2)2 * (((a2)2)2)2 mod n = ((((а2 * *а)2)2)2 * a) mod n.

При разумном накоплении промежуточных результатов потребуется только шесть умножений:

(((((((a2 mod n) * a) mod n)2 mod n)2 mod n)2 mod n) * a) mod n

Этот метод уменьшает трудоемкость вычислений до 1,5хк операций в среднем, где к - длина числа в битах.

Поскольку многие алгоритмы шифрования основаны на возведении в степень по модулю n, целесообразно использовать алгоритмы быстрого возведения в степень.

23

Контрольные вопросы:

1.Как можно выполнить вычисление степени числа а по модулю n?

2.В чём смысл гомоморфного отображения из кольца целых в кольцо целых?

3.Что такое приведение по модулю?

24

Практическое занятие № 7 Вычисления в конечных полях

Поле F есть множество, на котором определены операции сложения и умножения, удовлетворяющие требованиям: ассоциативности, коммутативности, дистрибутивности, существования аддитивного 0 и мультипликативной 1, аддитивных обратных и мультипликативных обратных для всех элементов за исключением 0 [2, 7].

Конечное поле F (p) с конечным числом р элементов играет важную роль в криптографии. В общем случае число элементов

P = qn,

где q - некоторое простое число и n≠1. Такие конечные поля называют полями Галуа и обозначают GF (qn) или GF (q) при n=1. (Эварист Галуа - французский математик начала XIX века.) Многие криптосистемы базируются на полях Галуа GF (q), где q - большое простое число.

Пример. Поле Галуа GF (5) имеет элементы 0, 1, 2, 3, 4 и описывается таблицами сложения и умножения (табл. 6):

25

Если q - простое число, то число a є [1, q - 1] является взаимно простым с q, и поэтому обратный элемент а-1 имеет единственное значение. Тем самым однозначно определяется операция деления.

Обозначим через GF *(q) множество всех ненулевых элементов поля GF (q). Некоторый элемент g из GF *(q)

называют образующим или порождающим элементом GF *(q), если для всех а из GF*(q) найдется такое целое х, что gx = a mod q. Всего имеется φ(q-1) образующих элементов g. Число х называют дискретным логарифмом элемента а по основанию g и модулю q. Вычисление дискретных логарифмов (когда заданы g, а и q) примерно такая же труднорешаемая задача, как и разложение на множители.

Еще один тип поля Галуа, используемый в криптографии, основывается на арифметике по модулю неприводимых многочленов степени n, чьи коэффициенты - целые числа по модулю q, где q - простое. Эти поля Галуа обозначают как GF (qn). Они имеют элементы, которые описываются многочленами степени не выше (n-1) в форме

а (х) = an-1Xn-1 + ... + a1, Х + а0.

Каждый элемент а (Х) является вычетом по модулю р(Х), где р(Х)- неприводимый многочлен степени n (т. е. р(Х) нельзя разложить на сомножители - многочлены степени меньше n).

Арифметические действия над коэффициентами ai выполняются по модулю q, а наивысшая степень X равна (n-1), так как выполняется приведение по модулю многочлена р(Х), имеющего старшую степень n.

Особый интерес представляют поля GF (2n). Здесь коэффициентами а, являются 0 и 1. Поэтому многочлен а(Х) степени не выше (n-1) можно представить как вектор из n двоичных цифр:

an-1an-2 ... a1a0

26

Каждый из n-битовых векторов соответствует конкретному элементу поля GF (2n).

Например, поле Галуа GF (23) имеет элементы (табл. 7):

Таблица 7

Организация вычислений в полях Галуа предполагает знание некоторых свойств многочленов и их корней в двоичном поле GF (2). Кратко приведем некоторые из них:

Свойство 1. Ненулевые элементы поля GF (2n) являются корнями обобщенного многочлена .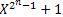

Свойство 2. Каждый многочлен р(Х) степени n, неприводимый над полем GF (2), является делителем двучлена 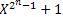, и каждый делитель двучлена , неприводимый над полем GF (2), имеет степень, равную n и менее.

Свойство 3. Все элементы поля GF (2n) можно получить как совокупность остатков от деления 100...00 на неприводимый многочлен р (Х), входящий в разложение двучлена (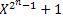). Эти остатки - корни двучлена (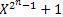), т. е. обращают его в нуль. Число остатков равно (2n-1).

Свойство 4. В поле GF (2n) существует примитивный элемент α, такой, что каждый ненулевой элемент поля GF (2n) может быть представлен как некоторая степень α, т.е. мультипликативная группа GF (2n) является циклической.

27

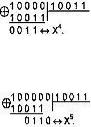
Пример. Определение элементов αi поля GF (24). Согласно свойству 1 ненулевые элементы поля GF (24) являются корнями обобщенного двучлена (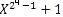) = = (X15+1). Двучлен (X15+1) можно представить в виде произведения неприводимых многочленов - сомножителей:

(X15+1) = P(Х1) * Р (Х2) * Р1(Х4) * Р2(Х4) * Р3(Х4),

где

P(Х1) = (X+1), Р(Х2) = Х2 + X + 1,

Р1(Х4) = Х4 + X + 1, Р2(Х4) = Х4 + Х3 +1,

Р3(Х4) = Х4 + Х3 + Х2 + X + 1

В соответствии со свойством 3 вычислим элементы αi поля GF (24) как совокупность остатков отделения 100...00 на неприводимый многочлен Р1(Х4) = Х4 + X + 1.

Процедура определения остатков

Делят на Р1(Х4) = Х4 + X + 1 <--> 10011 единицу с возрастающим числом нулей, т.е. делят одночлены Xj, где j = 0, 1, 2, 3 ... на многочлен (Х4 + X + 1). Степени одночленов Х0, Х1, Х2, Х3 меньше степени многочлена Р1(Х4), поэтому первые четыре остатка от деления на Р1(Х4) равны делимым, т.е. одночленам Х0, Х1, Х2, Х3. Для одночлена Х4 <--> 10000 получаем остаток

Для одночлена Х5 <--> 100000 получаем остаток

Схема вычисления остатков:

28