ФГБОУ ВПО "Воронежский государственный

технический университет"

Кафедра высшей математики

и физико-математического моделирования

Методические указания

для организации самостоятельной работы по математике

для студентов направлений 210100, 210400, 200100, специальности 210601 очной формы обучения

Воронеж 2011`

Составители: канд. физ.-мат. наук В.В. Посметьев, канд. физ.-мат. наук Л.Д. Кретова, канд. физ.-мат. наук Н.Б. Ускова

УДК 517.9

Методические указания для организации самостоятель­ной работы по математике для студентов направлений 210100, 210400, 200100, специальности 210601 очной формы обучения / ФГБОУ ВПО "Воронежский государственный технический университет"; сост. В.В. Посметьев, Л.Д. Кретова, Н.Б. Ускова. Воронеж, 2011. 38 с.

Методические указания разработаны с целью организации самостоятельной работы студентов над некоторыми разделами курса “Математика” и состоят из 6 разделов. В каждом из них изложен теоретический материал по предлагаемым для самостоятельного изучения темам, разработаны типичные примеры и задачи, сформулированы вопросы для самопроверки и задачи для самостоятельного решения.

Предназначены для студентов первого курса, 2 семестра.

Содержатся в электронном виде в текстовом редакторе Word 2003 в файле Кретова.doc.

Ил. 14. Библиогр.: 5 назв.

Рецензент канд. физ.-мат. наук, проф. Г.Е. Шунин

Ответственный за выпуск зав. кафедрой д-р физ.-мат. наук, проф. И.Л. Батаронов

Издается по решению редакционно-издательского сове­та Воронежского государственного технического университета

Ó ФГБОУ ВПО "Воронежский государственный технический университет", 2011

1. Экстремумы функции нескольких переменных. Наибольшее и наименьшее значения функции

Прежде чем приступить к изучению нового материала, вспомните необходимые и достаточные условия существования экстремумов функции одной переменной и методику нахождения точек экстремума и наибольшего и наименьшего значений функции.

Для функции двух переменных z = f(x, y) необходимым условием экстремума является равенство нулю частных производных и . Точки, в которых это условие выполняется, называются стационарными точками функции z(x,y).

Сформулируем достаточные условия экстремума для функции z = f(x,y). Пусть f(x,y) – функция, определенная в некоторой ε-окрестности точки (x ,y ) и имеющая в этой точке непрерывные частные производные второго порядка , , . Пусть, кроме того, в точке (x , y ) выполняются необходимые условия экстремума:

; . (1)

Если при этом в точке (x , y )

, (2)

то (x , y ) является точкой локального экстремума: при – минимума, при – максимума. Если в рассматриваемой стационарной точке D>0, то экстремума нет, а если D=0 – требуется дополнительное исследование.

Пример 1. Исследовать на экстремум функцию

.

Решение. Найдем частные производные первого порядка и приравняем их нулю:

Решив эту систему уравнений, найдем две стационарные точки A(0, 0) и A(1, 1).

Вычислим частные производные второго порядка:

Проверим достаточные условия в каждой стационарной точке. В точке A : , следовательно, экстремума нет. В точке A : , , следовательно, функция имеет минимум, равный

.

Если функция z= f(x, y) непрерывна в ограниченной замкнутой области, то она достигает своего наибольшего и наименьшего значения или в стационарных точках или на границе области. По этому для отыскания наибольшего и наименьшего значений функции необходимо:

- найти стационарные точки, принадлежащие рассматриваемой области и вычислить значения функции в этих точках (достаточные условия экстремума проверять не следует);

- найти наибольшее и наименьшее значения функции на линиях, образующих границу области;

- из всех полученных значений выбрать наибольшее и наименьшее.

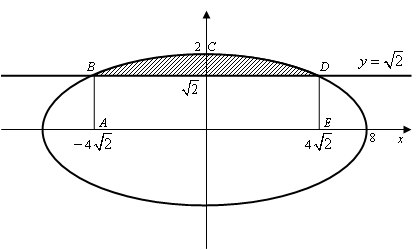
Пример 2. Найти наибольшее и наименьшее значения функции в замкнутой области, ограниченной областью Oy, прямой y = 2 и параболой при (рис. 1).

Решение.

1) Находим стационарные точки функции.

Решив систему уравнений

Получим две стационарные точки O(0, 0) и H(1, 1). Первая из них принадлежит границе области. Следовательно, если функция z принимает наибольшее (наименьшее) во внутренней точке области, то это может быть только в точке H(1, 1). Найдем z(H) = z(1, 1) = –1.

2) Исследуем функцию на границе области

а) на отрезке OA имеем x = 0, поэтому – возрастающая функция одной переменной y; наибольшее значение она принимает на концах отрезка OA. z(O ) = z(0;0) = 0; z(A) = z (0;2) = 12;

б) на отрезке AB имеем y = 2, следовательно, представляет функцию одной переменной x; ее наибольшее и наименьшее значения находятся среди ее значений в критических точках и на концах отрезка. Решая уравнение находим . Внутри отрезка имеется лишь одна критическая точка ; соответствующей точкой отрезка AB является точка Q( ;2). Итак, наибольшее и наименьшее значения функции z на отрезке AB находится среди ее значений в точках A, Q и B. Найдем

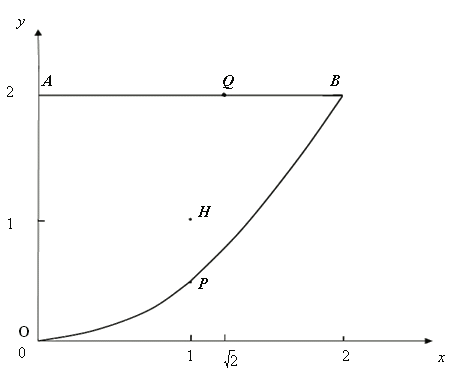
Рис. 1

; ;

в) на дуге OB параболы имеем .Решая уравнение , получим и ; соответствующими точками параболы являются точки O(0,0) и P(1;1/2). Таким образом, наибольшее и наименьшее значения функции z на дуге OB находятся среди ее значений в точках O, P и B. Найдем

.

3) сравнивая значения функции в точках H, O, A, Q, B и P, получим решение задачи

, .

Задания для самостоятельного решения

Выполните упражнения: [1], № 3272, 3273, 3277, 3281, 3282, 3286.

Контрольные вопросы

1. Почему понятие экстремума является локальным понятием?

2. Как сформулировать необходимые условия экстремума для функции n переменных?

3. Где достигается наибольшее и наименьшее значения функции?

4. Какие точки называются стационарными?

2. Деление многочленов.

Разложение многочленов на множители

При отыскании корней алгебраических уравнений и выделении целой части из дробно-рациональной функции нередко приходится выполнять операцию деление многочлена на многочлен.

Напомним, что при делении натурального числа на число всегда можно найти два других числа и таких, что

или . (3)

Число называется частным а – остатком от деления.

При делении многочлена степени на многочлен степени также всегда можно найти два других многочлена и , удовлетворяющие условиям:

или . (4)

Многочлен называется частным от деления и его степень равна разности степеней делимого и делителя, – остаток, степень которого меньше степени делителя. Соотношение (4) показывает, что неправильную рациональную дробь всегда можно представить в виде суммы многочлена и правильной рациональной дроби. Чтобы поделить многочлены, следует:

а) записать делимое и делитель по убывающим степеням ;

б) слагаемое, содержащее старшую степень делимого, разделить на старшую степень делителя;

в) полученное частное умножить на делитель и вычесть из делимого;

г) продолжить деление до тех пор, пока старшая степень делимого не станет меньше старшей степени делителя.

Пример 1. Разделить многочлен на квадратный двучлен .

Решение.

6x⁴ - 2x² + 3x – 1 │2x² - 4x

– │───────

6x⁴ - 12x³ 3x² + 6x + 11

––––––––––––––––––

12x³- 2x² + 3x - 1

–

12x³- 24x²

–––––––––––––––

22x² + 3x - 1

–

22x² - 44x

–––––––––––

47x - 1.

Следовательно:

.

Из школьного курса математики известно, что любой квадратный трехчлен может быть разложен на множители по формуле

, (4)

где и – действительные корни соответствующего квадратного уравнения. Если дискриминант квадратного уравнения меньше нуля, то его корни являются комплексными числами, а формула разложения сохраняет свой вид.

Покажем, что аналогичные формулы можно получить для многочленов любой степени. Рассмотрим произвольный многочлен степени

, (5)

где (k = 0, 1, …, n) – действительные числа, а независимая переменная x может принимать как действительные, так и комплексные значения. Число называют корнем многочлена , если . Корни многочлена, очевидно, совпадают с корнями алгебраического уравнения

. (6)

Теорема 1. Всякое алгебраическое уравнение (2.3) при имеет по крайней мере одно решение.

Эта теорема (ее называют основной теоремой алгебры) доказана в курсе высшей алгебры и из нее следует, что любой многочлен ненулевой степени имеет хотя бы один корень.

Для выяснения количества корней многочлена докажем следующее утверждение.

Теорема 2. При делении многочлена на по­лучается остаток, равный .

Доказательство. Из рассмотренного выше правила де­ления многочленов следует, что частным от деления будет многочлен -й степени , а остатком – многочлен нулевой степени, т.е. число . Результат деления можно пред­ставить соотношением:

.

Отсюда

.

Полагая , получаем , что и требовалось доказать.

Следствие. Если – корень многочлена (2.2), то делится на без остатка, т.е.

. (7)

Применяя теоремы 1 и 2 к многочлену , полу­чим

.

где – корень многочлена , а следовательно и много­члена .

Продолжая этот процесс выделения корней, получим формулу

. (8)

Если среди корней многочлена есть кратные, то (2.5) принимает вид:

,

где – кратность соответствующего корня, причем .

Если многочлен имеет комплексные корни , то, перемножая соответствующие им скобки, получим

,

где , , причем . Следовательно, каждой паре взаимно сопряженных комплексных корней мно­гочлена в формуле разложения можно поставить в соответст­вие приведенный квадратный трехчлен с действительными коэффициентами и отрицательным дискриминантом. Если эти комплексные корни имеют кратность , то соответствующий квадратный трехчлен в формуле разложения имеет степень .

Итак, всякий многочлен с действительными коэффициентами может быть единственным образом разложен на множители по формуле:

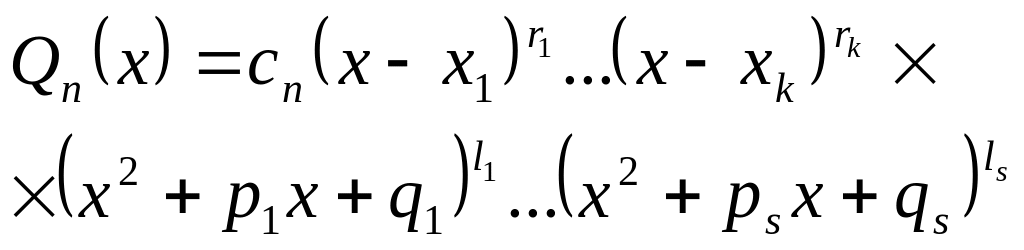, (9)

где x₁, x₂, …, x_k – действительные корни многочлена ; p₁, q₁, …, p_s, q_s – действительные числа; каждый из квадрат­ных трехчленов имеет только комплексные корни; r₁, r₂, …, r_k, l₁, l₂, …, l_s– целые положительные числа, причем .

Заметим, что при отыскании действительных корней алгебраических уравнений можно использовать теорему:

Теорема 3. Все целые корни приведенного алгебраиче­ского уравнения с целыми коэффициентами являются делите­лями его свободного члена.

Пример 2. Решить уравнение .

Решение. Подставляя делители свободного члена в уравнение, получаем, что его корнями являются числа: 1, -2, -3.

Пример 3. Разложить на множители многочлен

.

Решение. Нетрудно убедиться, что один из делителей свободного члена является корнем многочлена . После деления на получим

.

Решения полученного биквадратного уравнения имеют вид: , . Отсюда , , , . Итак, многочлен имеет действительный корень , кратность которого равна 2, действительный простой корень и два простых взаимно-сопряженных комплексных корня . Тогда из (9) следует:

Задания для самостоятельного решения

1. Решить уравнения:

а) ;

б) .

2. Разложить на множители многочлены:

а) ; б) .

3. Выполнить деление многочленов:

а) ;б) .