Нормализованная матрица планирования
Эксперты |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Tj |
I |
4 |
2 |
1 |
6 |
5 |
7 |
3 |
|
|
II |
4 |
1,5 |
1,5 |
6 |
5 |
7 |
3 |
2 |
0,5 |
III |
4 |
2 |
1 |
5 |
6 |
7 |
3 |
|
|
IV |
4 |
1 |
2 |
6,5 |
5 |
6,5 |
3 |
2 |
0,5 |
V |
4 |
2 |
1 |
6 |
4 |
7 |
4 |
3 |
2 |
VI |
3,5 |
2 |
1 |
5,5 |
5,5 |
7 |
3,5 |
2+2 |
1 |
VII |
4 |
2,5 |
1 |
6 |
5 |
7 |
2,5 |
2 |
0,5 |
VIII |
4 |
2 |
1 |
6,5 |
5 |
6,5 |
3 |
2 |
0,5 |
S= |
31,5 |
15 |
9,5 |
47,5 |
40,5 |
55 |
25 |
|
|
Ранги |
4 |
2 |
1 |
6 |
5 |
7 |
3 |
|
|
Критерии
По данным матрицы ранжирования производится оценка согласованности мнения экспертов с помощью конкордации по формуле 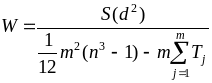(2):
,
(2)
где
,
,
,
ti - число повторений i-го ранга в j-ой строке матрицы,
aji - ранг j-го эксперта i-го критерия,
m - количество экспертов,
n - количество критериев.
Если матрица ранжирования не содержит совпавших рангов, то коэффициент конкордации определяется по формуле (3):
.
(3)
Соответственно в рассмотренном примере W = 0,945.
Для оценки значимости коэффициента конкордации W используется 2 - критерий Пирсона, расчетная величина которого определяется по формуле (4) или (5):
,
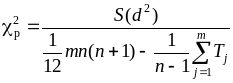(4)
.
(5)
При числе степеней свободы f = n - 1 определяется табличное (критическое) значение 2табл (табл. 3) и сравнивается с расчетным. Если 2расч > 2табл, то гипотеза о наличии согласия экспертов принимается.
Таблица 3
Табличные значения 2 - критерия Пирсона в зависимости
от f степеней свободы
f |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
2 |
3,841 |
5,991 |
7,815 |
9,488 |
11,070 |
12,592 |
14,067 |
15,507 |
f |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
2 |
16,919 |
18,307 |
19,675 |
21,026 |
22,362 |
23,685 |
24,996 |
26,296 |
f |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
2 |
27,587 |
28,869 |
30,144 |
31,410 |
32,671 |
33,924 |
35,172 |
36,415 |
В нашем случае, 2расч = 45,363, а при f = 6, 2табл = 12,592. Из этого следует, что гипотеза о наличии согласия экспертов принимается.
Для большей наглядности полученные результаты представляются на гистограмме ранжирования, где по оси абсцисс наносятся номера критериев в порядке убывания или возрастания обобщенных рангов, а на оси ординат для каждого критерия откладывается соответственно величина обобщенной суммы рангов, каждая, по существу, характеризует меру согласованности экспертов в присвоении данного критерия найденного ранга (рис. 1).
Рис. 1. Гистограмма ранжирования
Как видно из гистограммы, распределение равномерное, убывание влияния критериев монотонное. Поэтому сделаем вывод о значимости критериев выбора рационального программно-аппаратного обеспечения. Пусть Р(i) - будет важность i-го критерия, тогда получим: P(3) > P(2) > P(7) > P(1) > P(5) > P(4) > P(6), то есть по убыванию важности критерия они имеют вид:
а) надежность;
б) функциональные характеристики;
в) логические функциональные характеристики;
г) стоимость;
д) защита информации;
е) срок гарантии аппаратного обеспечения;
ж) организация обучения обслуживающего персонала.