
3. Термодинамика
3.1. Найти удельные
теплоемкости
![]() и
и
![]() ,
а также показатель адиабаты смеси,
содержащей кислород массой
,
а также показатель адиабаты смеси,
содержащей кислород массой
![]() и метанол массой
и метанол массой
![]() .
Химическая формула метанола
.
Химическая формула метанола
![]() .
.
Дано: |
СИ: |
Решение: |
|
|
Удельной
теплоемкостью
Теплоемкость
1 моля вещества соответственно
называется молярной
теплоемкостью
|
|
||
Две эти величины
связаны соотношением:
Для нахождения
где
Учитывая (1), получаем:
Разделим на
Найдем удельную
теплоемкость газа с учетом зависимости
молярной теплоемкости от числа степеней
свободы газа:
Т.о., получаем, что удельная теплоемкость смеси газов равна:
Воспользовавшись
уравнением Майера, получим выражение
для молярных теплоемкостей:
Показатель адиабаты смеси газов найдем по формуле:
|
||
Ответ:
|
||
3.2. Степень
диссоциации газообразного водорода
![]() .
Найти удельную теплоемкость
.
Найти удельную теплоемкость
![]() такого частично диссоциировавшего
водорода.
такого частично диссоциировавшего
водорода.
Дано: |
СИ: |
Решение: |
|
|
Частично диссоциировавший водород состоит из атомарного водорода (H) и молекулярного |
|
||
водорода (H2). Количество вещества атомарного водорода в такой смеси:
где
- степень диссоциации,
- масса смеси,
Количество вещества молекулярного водорода:
Удельную теплоемкость частично диссоциировавшего газа найдем из следующих соображений: для нагревания такой смеси на необходимо затратить количество теплоты:
Отсюда, удельная теплоемкость смеси:
Молярная теплоемкость атомарного водорода
Следовательно
|
||
Ответ:
|
||
3.3. Мощность,
развиваемая двигателем самолета ИЛ-96
на скорости
![]() ,
равна
,
равна
![]() .
При этом за час в среднем расходуется
.
При этом за час в среднем расходуется
![]() топлива, обладающего удельной теплотой
сгорания
топлива, обладающего удельной теплотой
сгорания
![]() .
Найти КПД двигателя.
.
Найти КПД двигателя.
Дано: |
СИ: |
Решение: |
|
|
КПД двигателя равен отношению полезной работы к величине полученной от сгорания топлива энергии:
|
|
||
Работу двигателя найдем, исходя из развиваемой им мощности:
Работа, совершаемая
двигателем на пути
Количество тепла, получаемого при сгорании топлива в единицу времени, равно:
Для решения
задачи пересчитаем расход топлива,
приходящийся на единицу длины. Так
как при скорости
расход составляет
Т.о.,
|
||
Ответ:
|
||
3.4. Под поршнем
находится
![]() азота. Какое количество теплоты
необходимо, чтобы нагреть азот на
азота. Какое количество теплоты
необходимо, чтобы нагреть азот на
![]() ?
Насколько при этом поднимется поршень,
если его масса
?
Насколько при этом поднимется поршень,
если его масса
![]() ,
площадь поперечного сечения
,
площадь поперечного сечения
![]() ?
Давление над поршнем равно
?
Давление над поршнем равно
![]() .
.
Дано: |
СИ: |
Решение: |
|
|
При изобарном
процессе количество теплоты можно
выразить через теплоемкость при
постоянном давлении
где
число
степеней свободы
|
|
||
двухатомный.
Давление определяется атмосферным давлением и давлением поршня
|
||
Ответ:
|
||
3.5. Вода выходит
из водяной рубашки двигателя внутреннего
сгорания нагретой до
![]() ,
после чего поступает в радиатор, где
охлаждается до
,
и снова подается в водяные рубашки
цилиндров двигателя. Какое количество
тепла уносится водой от двигателя
ежеминутно, если производительность
насоса, движущего воду, равна
,
после чего поступает в радиатор, где
охлаждается до
,
и снова подается в водяные рубашки
цилиндров двигателя. Какое количество
тепла уносится водой от двигателя
ежеминутно, если производительность
насоса, движущего воду, равна
![]() ?
?
Дано: |
СИ: |
Решение: |
|
|
|
|
||
Ответ:
|
||
3.6. Генератор
излучает импульсы сверхвысокой частоты
с энергией в каждом импульсе
![]() .
Частота повторения импульсов
.
Частота повторения импульсов
![]() .
Коэффициент полезного действия генератора
.
Коэффициент полезного действия генератора
![]() .
Сколько литров воды в час надо прогонять
через охлаждающую систему генератора
для того, чтобы вода нагревалась не выше
чем на
?
.
Сколько литров воды в час надо прогонять
через охлаждающую систему генератора
для того, чтобы вода нагревалась не выше
чем на
?
Дано: |
СИ: |
Решение: |
|
|
Полная энергия излучения генератора за время :
За то же время в виде тепла в генераторе выделится энергия:
|
|
||
идущая на нагревание воды. Тогда объем воды будет равен
В час это составит:
|
||
Ответ:
|
||
3.7.
![]() кислорода, находящегося при нормальных
условиях, сжимается до объема
кислорода, находящегося при нормальных
условиях, сжимается до объема
![]() .
Найти давление и температуру кислорода
после сжатия, если оно происходит: 1)
изотермически; 2) адиабатически. Найти
работу в каждом случае.
.
Найти давление и температуру кислорода
после сжатия, если оно происходит: 1)
изотермически; 2) адиабатически. Найти
работу в каждом случае.
Дано: |
СИ: |
Решение: |
|
|
1) Изотермический
процесс:
По закону Бойля-Мариотта:
Используя уравнение Менделеева-Клапейрона, получаем:
Работа над газом:
|
|
||
2) Для адиабатного процесса давление и объем связаны уравнением Пуассона:
Согласно уравнению Менделеева-Клапейрона:
Согласно первому началу термодинамики:
|
||
Ответ:
|
||
3.8. Один моль
идеального газа перевели из состояния
1 в состояние 2 изохорно так, что его
давление уменьшилось в 1,5 раза, а затем
изобарно нагрели до первоначальной
температуры
![]() .
При этом была совершена работа
.
При этом была совершена работа
![]() .
Найти температуру
.
.
Найти температуру
.
Дано: |
СИ: |
Решение: |
|
|
В ходе процесса на изохорном участке работа не совершается, поэтому определим работу в изобарном процессе:
(использовалось уравнение состояния идеального газа)
Для нахождения
Отсюда:
|
|
||
Ответ:
|
||
3.9. Моль двухатомного идеального газа, первоначально находившийся при нормальных условиях, переводят в состояние с вдвое большими объемом и давлением. Процесс перевода слагается из двух участков – изобары и изохоры. Какое количество теплоты поведено к газу?
Дано: |
СИ: |
Решение: |
|
|
Учитывая, что
Аналогично определяем
|
|
||
|
||
Ответ:
|
||
3.10. Над молем
идеального газа совершают замкнутый
цикл, состоящий из двух изохор и двух
изобар. Температуры в точках 1
и 3
равны
![]() и
и
![]() .
Определить работу, совершенную за цикл,
если известно, что точки 2
и 4
лежат на одной изотерме.
.
Определить работу, совершенную за цикл,
если известно, что точки 2
и 4
лежат на одной изотерме.
Дано: |
СИ: |
Решение: |
|
|
Работа за цикл равна:
Используя рисунок, получаем:
Следовательно:
Для участка
|
|
||
для участка
Тогда:
|
||
Ответ:
|
||
3.11. На рисунке
изображены два замкнутых цикла:
![]() и
и
![]() .
Оба цикла проведены с идеальным
одноатомным газом. У какого из циклов
к.п.д. выше и во сколько раз?
.
Оба цикла проведены с идеальным
одноатомным газом. У какого из циклов
к.п.д. выше и во сколько раз?
Дано: |
СИ: |
Решение: |
|
|
К.п.д. цикла равен:
На
В цикле
тепло подводится на участке
|
|
||
В изохорном
процессе
Для изобарного процесса
Тогда:
В цикле
теплота подводится в процессе
работа определяется из графика, как площадь трапеции:
тогда:
Так как
и
|
||
Ответ:
|
||
3.12. Тепловую машину,
работающую по циклу Карно с к.п.д.
![]() ,
используют при тех же тепловых резервуарах
как холодильную машину. Найти ее
холодильный коэффициент
,
используют при тех же тепловых резервуарах
как холодильную машину. Найти ее
холодильный коэффициент
![]() .
.
Дано: |
СИ: |
Решение: |
|
|
Для цикла Карно к.п.д.:
|
|
||
или
Холодильным коэффициентом называется отношение:
|
||
Ответ:
|
||
3.13. Идеальный газ с показателем адиабаты совершает цикл, состоящий из двух изохор и двух изобар. Найти к.п.д. такого цикла, если температура газа возрастает в раз как при изохорическом нагреве, так и при изобарическом расширении.
Дано: |
СИ: |
Решение: |
|
|
К.п.д. цикла вычисляется по формуле:
Аналогично задаче 3.10 получаем:
|
|
||
Теплота в цикле
подводится в процессах
тогда
Учитывая, что:
тогда:
|
||
Ответ:
|
||
3.14. Идеальный газ с показателем адиабаты совершает прямой цикл, состоящий из адиабаты, изобары и изохоры. Найти к.п.д. цикла, если при адиабатическом процессе объем идеального газа: а) увеличивается в раз; б) уменьшается в раз.
Дано: |
СИ: |
Решение: |
|
|
|
К.п.д. цикла находим по формуле:
Теплообмен происходит на участках 1-2 и 3-1. Учитывая выражения для теплоемкостей идеального газа при постоянных давлении и объеме:
получаем: |
|
1)
|
|||
количество теплоты, получаемой и отдаваемой на участках 1-2 и 3-1:
Для изобарного процесса:
Для адиабатного процесса:
Тогда, учитывая, что
|
|||
2)
|
Теплообмен происходит на участках 1-2 и 2-3, количество теплоты, получаемой и отдаваемой при этом газом равно:
|
||
Для изобарного процесса:
Для адиабатного процесса:
Тогда
|
|||
Ответ: 1)
2)
|
|||
3.15. Гелий массы
![]() адиабатически расширили в 3 раза и затем
изобарно сжали до первоначального
объема. Найти приращение энтропии в
этом процессе.
адиабатически расширили в 3 раза и затем
изобарно сжали до первоначального
объема. Найти приращение энтропии в
этом процессе.
Дано: |
СИ: |
Решение: |
|
|
Приращение
энтропии определяется формулой:
где
|
|
||
Разделим уравнение на :
Согласно уравнению Менделеева-Клапейрона:
откуда:
Тогда
Для
следовательно:
|
||
Ответ:
|
||
3.16. Найти КПД цикла Карно.
Дано: |
СИ: |
Решение: |
|
|
Вид цикла Карно на диаграмме P-V зависит от свойств совершающего цикл вещества. В него входит два изотермических процесса и два адиабатных. Для идеального газа цикл представлен на рисунке
При
изотермическом процессе внутренняя
энергия идеального газа остаётся
постоянной. Поэтому количество
полученной газом теплоты
где – масса идеального груза в |
|
||
машине.
Количество отдаваемой холодильнику
теплоты
Для того чтобы цикл был замкнутым, состояния 1 и 4 должны лежать на одной и той же адиабате. Отсюда получаем условие
Состояния 2 и 3 удовлетворяют аналогичному условию:
Объединяя эти соотношения, получаем:
Подставив
соответствующие значения
|
||
Ответ:
|
||
3.17. Найти к.п.д. цикла двигателя Дизеля, если показатель степени адиабаты равен .
Дано: |
СИ: |
Решение: |
|
|
Цикл Дизеля двигателя внутреннего сгорания осуществляется следующим образом:
|
рис. исправлен
|
||
Главное отличие заключается в том, что применяется весьма большая степень сжатия (до 30 – 35 атмосфер и более). Так как сжатие это происходит приблизительно адиабатически, то достигается большое повышение температуры. Этого повышения температуры достаточно для воспламенения горючей смеси, так что двигатель Дизеля не требует воспламенения горючей смеси с помощью искры. Горючая смесь взбрызгивается в цилиндр по окончании сжатия, причем взбрызгивается она постепенно, что обуславливает ее относительно медленное сгорание при изобарном расширении. Эти особенности двигателя Дизеля позволяют получить более высокий КПД, чем у четырехтактных двигателей с воспламенением искрой. Кроме того, двигатели Дизеля работают на более тяжелом топливе (нефть).
Для определения
полной работы
где
Так как по условию сгорание смеси происходит изобарно (ветвь ), то
Процесс, связанный с отдачей тепла (ветвь ), происходит изохорно, следовательно:
Воспользовавшись
этими выражениями для
и
,
и связью
Коэффициент полезного действия цикла Дизеля равен
Пользуясь уравнением адиабат и изобар, можно привести это выражение к следующему виду:
Т.о.,
КПД цикла Дизеля определяется
показателем адиабаты газа и характером
двух сжатий. Отношение
|
||
Ответ:
Или . |
||
3.18. Найти к.п.д. цикла двигателя Отто, если показатель степени адиабаты равен .
Дано: |
СИ: |
Решение: |
|
|
В цикле Отто газовых и карбюраторных четырехтактных двигателей внутреннего сгорания сжимается рабочая смесь, приготовленная вне цилиндров (газ-воздух или пары легкого топлива-воздух): : всасывание рабочей смеси, которое можно считать изобарным; : адиабатическое сжатие рабочей |
|
||
смеси, в конце сжатия происходит зажигание горючей смеси от электрической искры; : быстрое возрастание температуры и давления продуктов сгорания (практически при постоянном объеме); : адиабатное расширение продуктов сгорания (рабочий ход поршня); : в конце расширения открывается выпускной клапан, происходит падение давления в цилиндре при постоянном объеме; : выталкивание поршнем продуктов сгорания. Подсчитаем полную работу, совершаемую в цикле. Работы, совершаемые при первом и последнем тактах ( и ), равны друг другу и противоположны по знаку, что непосредственно вытекает из того, что оба эти такта изображаются одной и той же прямой, проходимой в противоположных направлениях. Работы в изохорных процессах и равны нулю. Таким образом, работа, совершаемая в цикле, складывается из работ на ветвях и . При адиабатическом сжатии совершается работа
где – масса газа, находящегося в цилиндре, его молекулярный вес. При адиабатическом расширении совершается работа:
откуда полная работа
Учитывая уравнение Пуассона для адиабатного процесса
Кроме того,
Воспользовавшись этими соотношениями, перепишем (1) в виде:
Зная, что
Определим КПД цикла.
Количество тепла
Тогда искомый КПД цикла:
Пользуясь соотношением (2), можно КПД цикла записать в виде:
Величина
Четырехтактные двигатели, работающие по указанному циклу, имеют весьма широкое применение; бензиновые автомобильные двигатели работают по этому циклу. Обычно на один вал работают несколько цилиндров (четыре и более). Рабочая фаза каждого цилиндра сдвинута относительно рабочей фазы следующего цилиндра на одну и ту же долю периода, чем достигается плавность хода. |
||
Ответ:
или . |
||
3.19. Найти КПД рабочего цикла воздушно-реактивного двигателя.
Дано: |
СИ: |
Решение: |
|
|
Работе этого двигателя можно сопоставить цикл Брайтона, изображенный на рис.1. Поступающий и диффузор А воздух (рис.2) проходит из более узкой головной части в расширенную, благодаря чему скорость воздуха понижается. При этом в силу уравнения Бернулли давление воздуха |
|
||
повышается. Т.о.,
происходит сжатие воздуха, совершаемого
в свободной струе перед двигателем
за счет скоростного напора (динамическое
сжатие) и в компрессоре (механическое
сжатие). Этот процесс изображен на
рис.1 адиабатой (точнее, политропой)
В камере сгорания
происходит нагревание рабочей смеси
при постоянном давлении (
В газовой турбине
и реактивном сопле С происходит
дальнейшее адиабатическое расширение
Практически цикл
остается незамкнутым, но на схеме его
можно замкнуть, полагая, что рабочее
вещество вновь сжимается до объема
Коэффициент полезного действия цикла:
Так как сгорание и охлаждение смеси происходит при постоянном давлении, то
откуда:
Из уравнений адиабат и имеем:
откуда
Пользуясь этим соотношением между температурами, преобразовываем выражение для КПД к следующему виду:
Таким образом,
промежуточные температуры
Отношение
температур
откуда:
Последнее
выражение показывает, что КПД
воздушно-реактивного двигателя
определяется лишь степенью сжатия
Так как в воздушно-реактивных двигателях, построенных, но указанной схеме, сжатие невелико, то их КПД мал. |
||
Ответ:
или
|
||
3.20. В паровой
турбине расходуется
![]() дизельного топлива на
дизельного топлива на
![]() .
Температура пара, поступающего в турбину,
.
Температура пара, поступающего в турбину,
![]() .
Температура холодильника
.
Температура холодильника
![]() .
Вычислить фактический КПД турбины и
сравнить его с КПД идеальной тепловой
машины, работающей при тех же условиях.
Удельная теплота сгорания дизельного
топлива равна
.
Вычислить фактический КПД турбины и
сравнить его с КПД идеальной тепловой
машины, работающей при тех же условиях.
Удельная теплота сгорания дизельного
топлива равна
![]() .
.
Дано: |
СИ: |
Решение: |
|
|
Запишем выражение для КПД идеальной тепловой машины:
Фактический КПД равен:
|
|
||
где количество теплоты вычисляется через удельную теплоту сгорания дизельного топлива:
Следовательно:
|
||
Ответ:
|
||
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Волькенштейн В.С. Сборник задач по общему курсу физики / В.С. Волькенштейн. 8–е изд., М.: Машиностроение, 2005. 389 с.
Чертов А.Г. Задачник по физике / А.Г. Чертов, А.А. Воробьев. 8-е изд. перераб. и доп. М.: Издательство физико-математической литературы, 2009. 640 с.
Гофман Ю.В. Законы, формулы, задачи физики: справочник / Ю.В. Гофман, Киев: Наукова думка, 1977.576 с.
Иродов И.Е. Задачи по общей физике / И.Е. Иродов. 2–е изд, М.-С-Пб.: Лань, 2003. 416 с.
Холидей Д. Вопросы и задачи по физике: пособие для студентов пед. институтов. / Д. Холидей, Р. Резник. Пер. с англ. С.Н. Немирова. М.: Просвещение, 1969. 239 с.
Сборник задач по физике / Л.П. Баканина, В.Е. Белонучкин, С.М. Козел, Н.Н. Колачевский, Г.И. Косоуров, И.П. Мазанько. 2–е изд. перераб. М.: Наука. Главная редакция физико-математической литературы, 1971. 416 с.
Задачи по физике для поступающих в вузы: учеб. пособие / Г.А. Бендриков, Б.Б. Буховцев, В.В. Керженцев, Г.Я. Мякишев. 5-е изд. перераб. М.: Наука. Главная редакция физико-математической литературы, 1985. 400 с.
Сборник задач и вопросов по физике для среднеспециальных учебных заведений / Р.А. Гладкова, В.Е. Добронравов, Л.С. Жданов, Ф.С. Цодиков. М.: Наука. Главная редакция физико-математической литературы, 1972. 368 с.
Сборник задач по физике / М.С. Цедрик, А.С. Микулич, И.Ф. Савицкая, Г.А. Загуста, Г.П. Макеева. Минск: «Высшая школа». 1968. 280 с.302.
Агапитова Н.В. Энтропия. II начало термодинамики. Тепловые двигатели. Теоретические и практические материалы: метод. указания / Н.В. Агапитова, П.И. Деркачева, В.С. Железный. Воронеж: ВГТУ, 2007. 102 с.56.
Фирганг Е.В. Руководство к решению задач по курсу общей физики: учеб. пособие для ВТУЗов / Е.В. Фирганг. М.: Высшая школа, 1977. 351 с.12.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к практическим занятиям по дисциплине «Физика»
для студентов специальностей

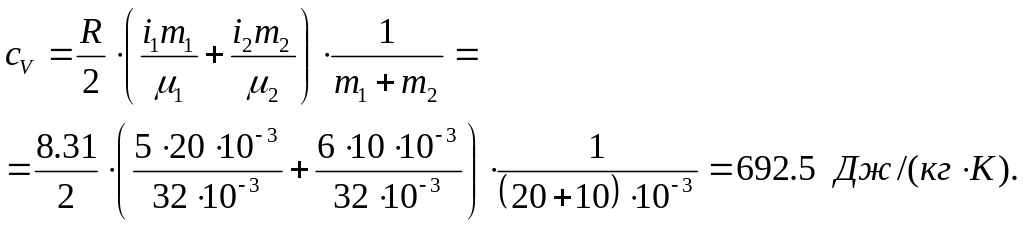
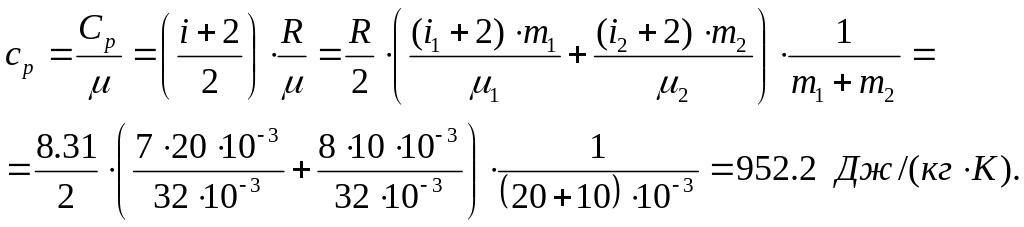
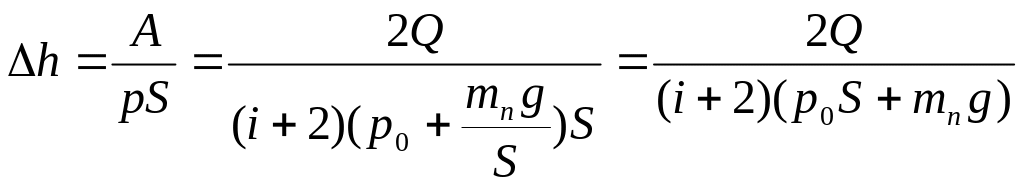 ,
,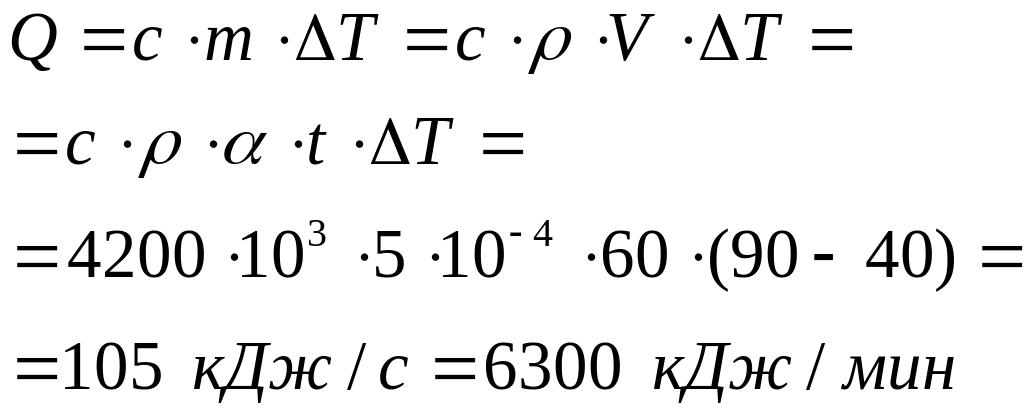
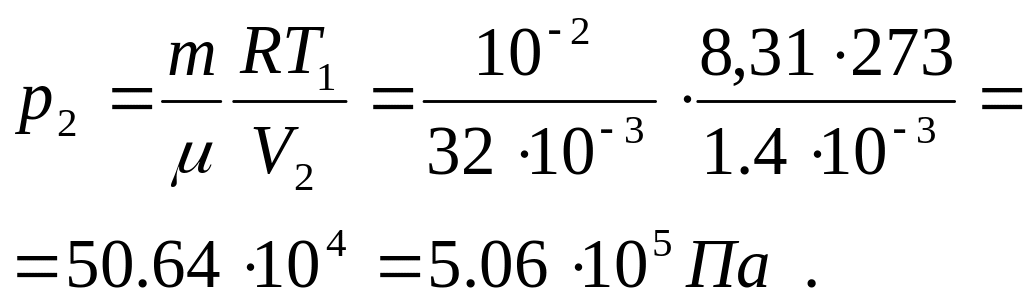
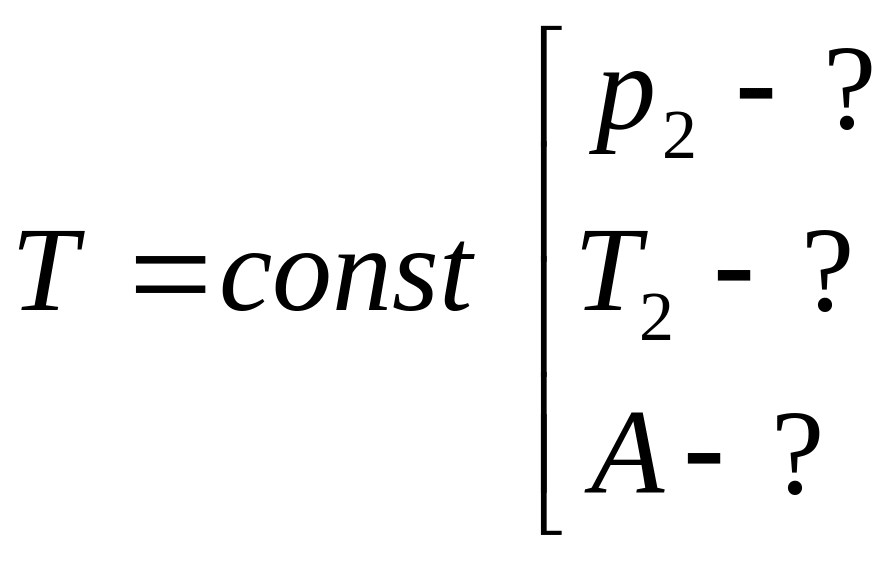
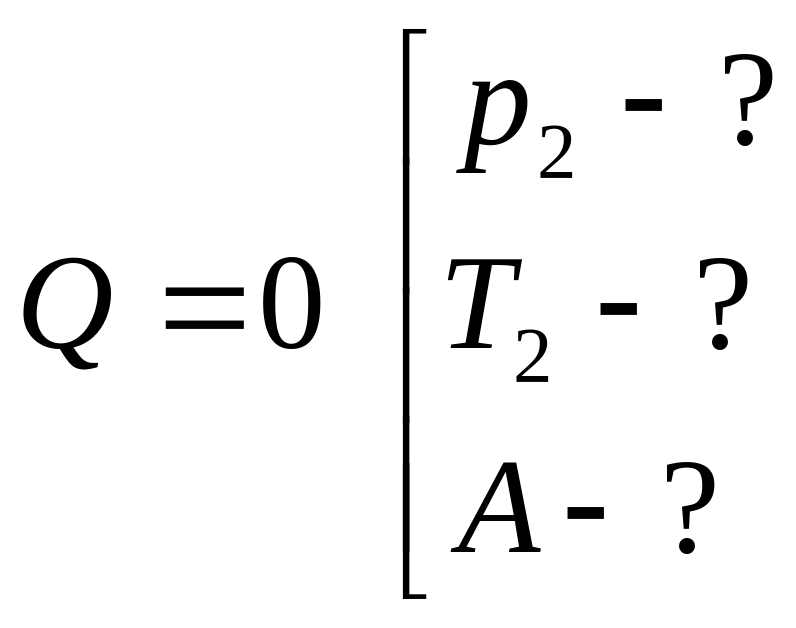
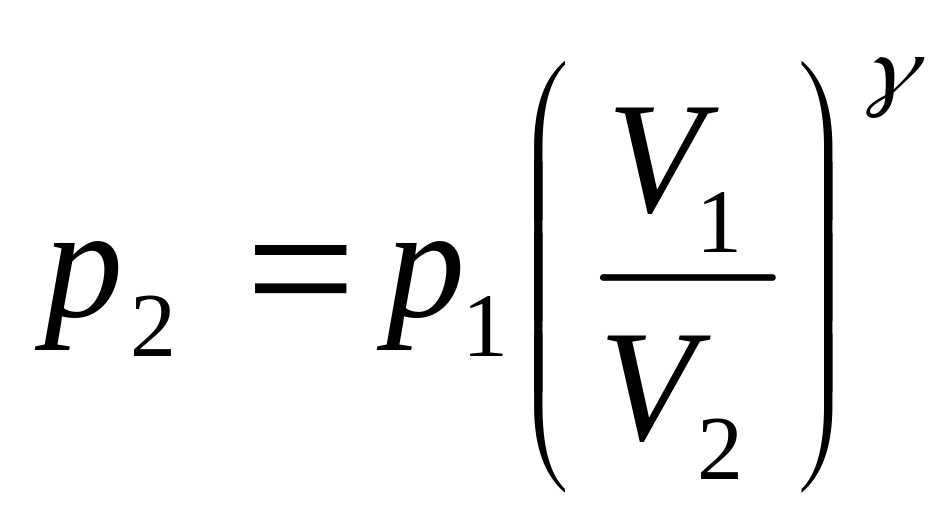 ,
где
,
где

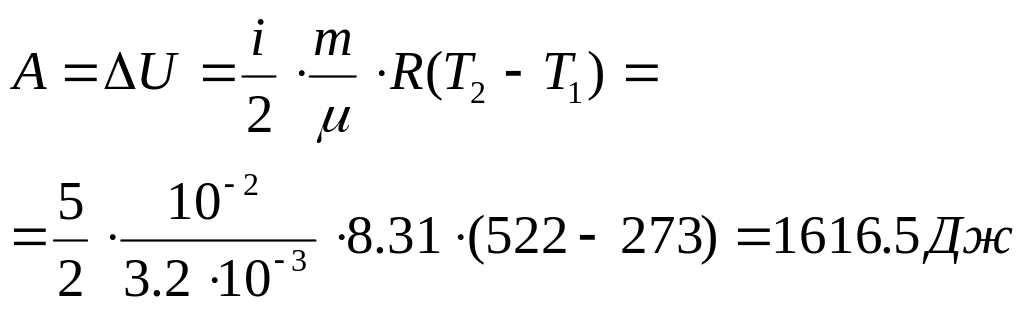
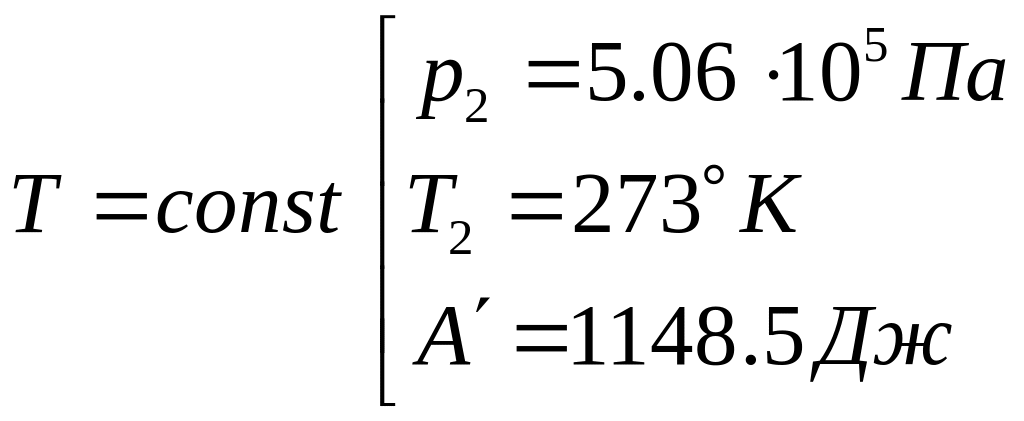
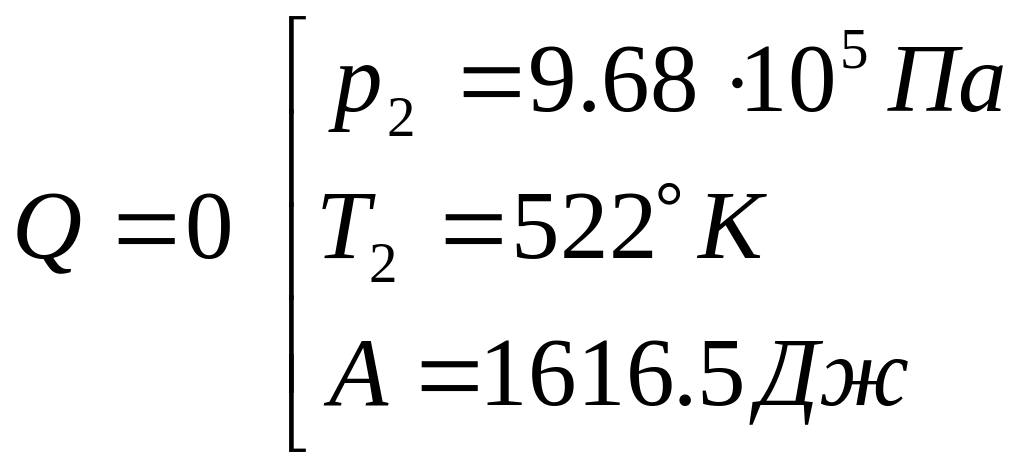
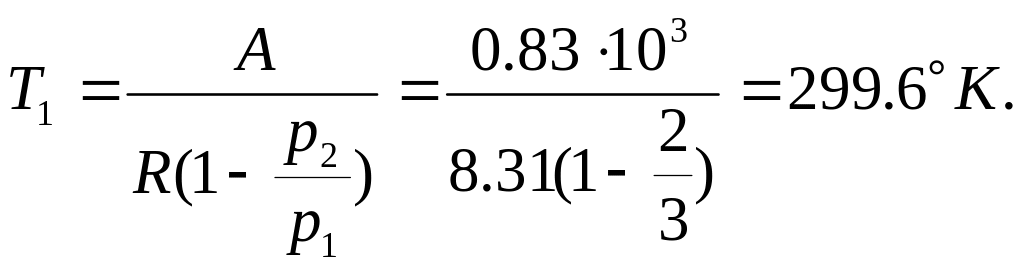


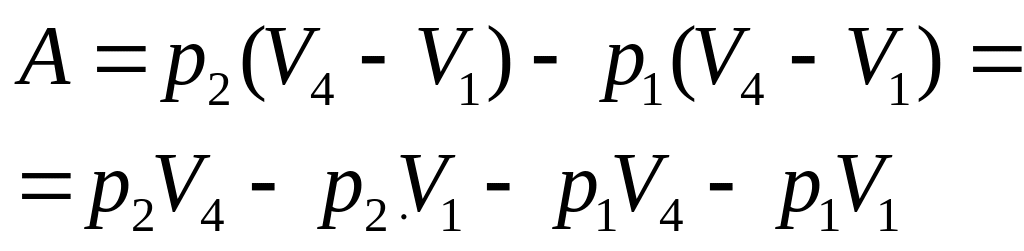


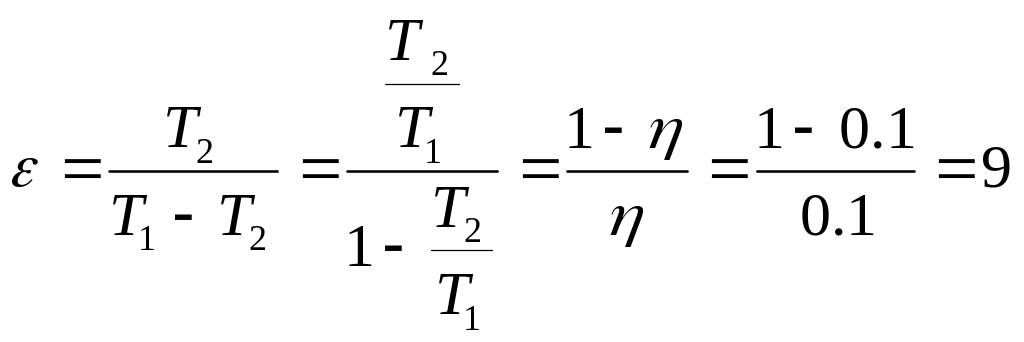 .
.
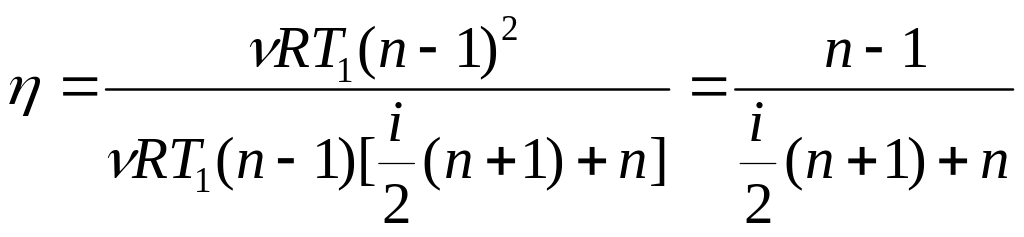 ;
;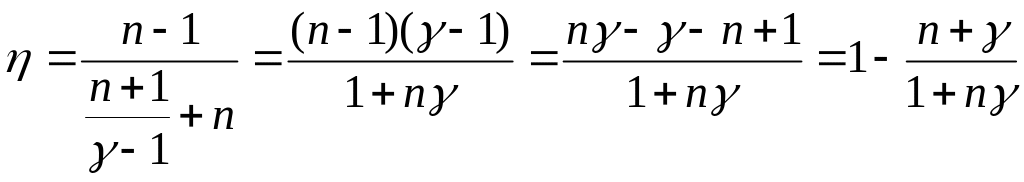 .
.
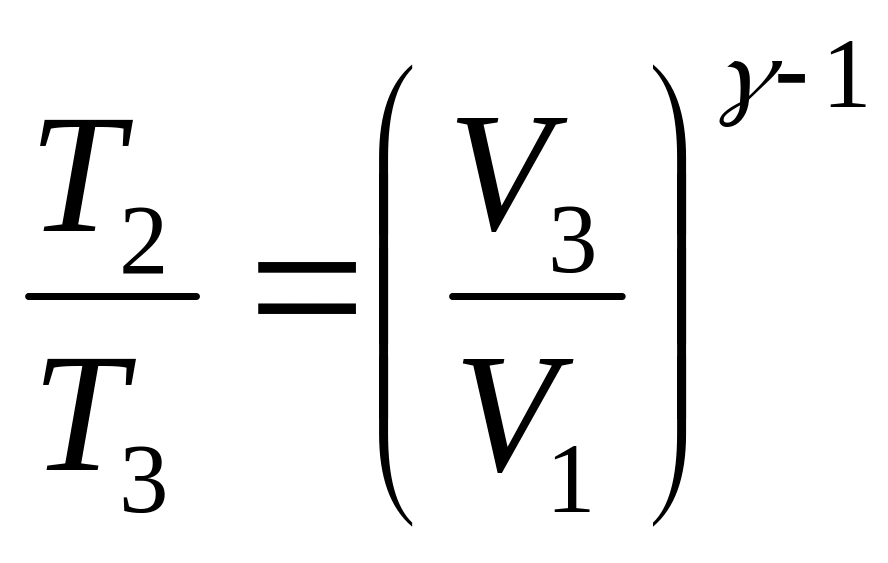 или
или
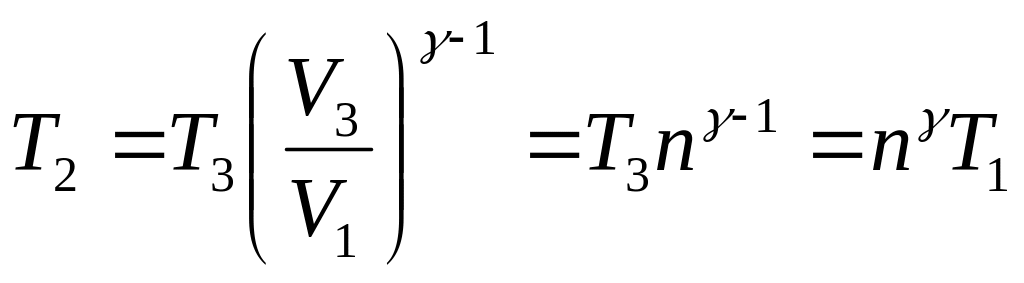 .
.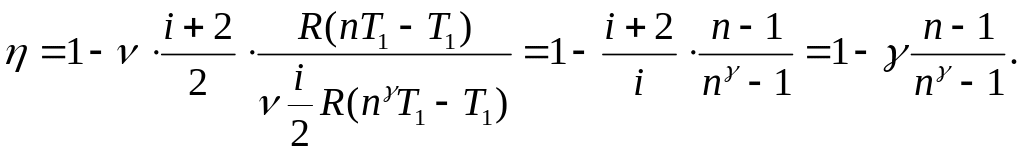

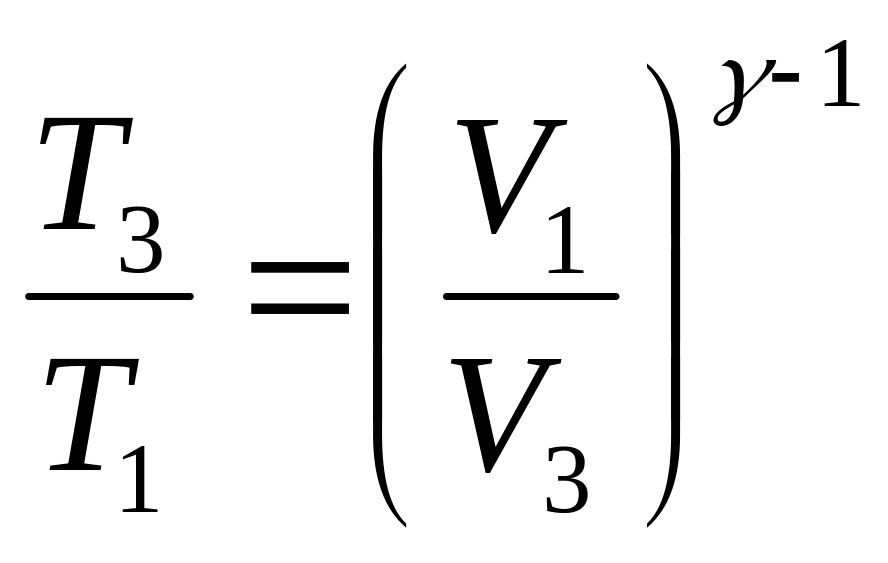 или
или
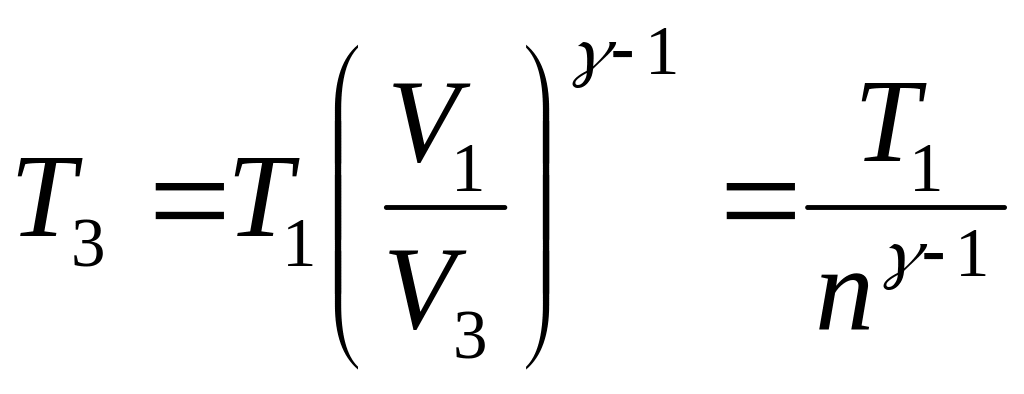 .
.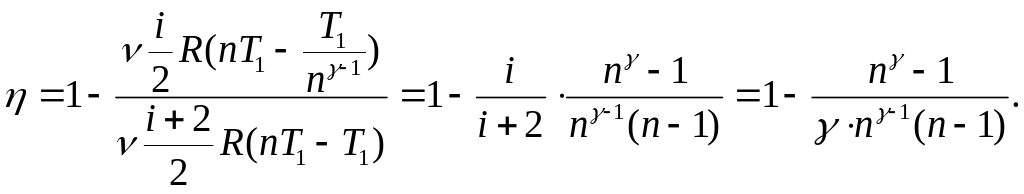

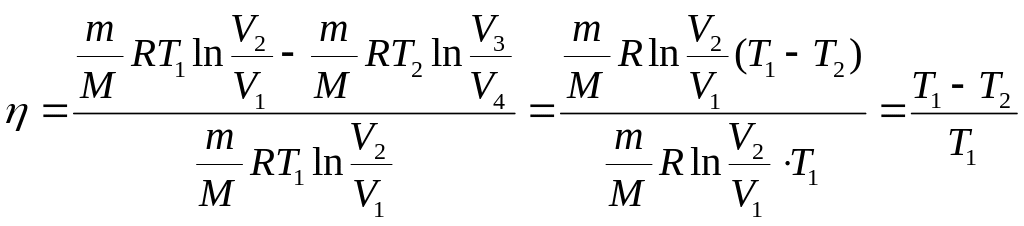 .
.


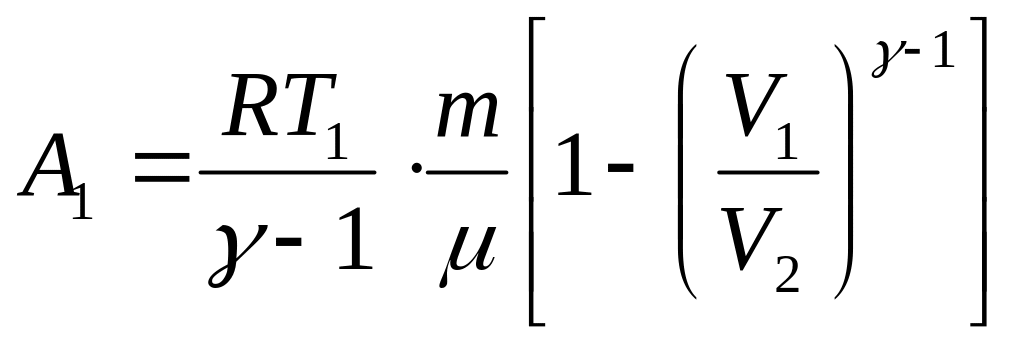
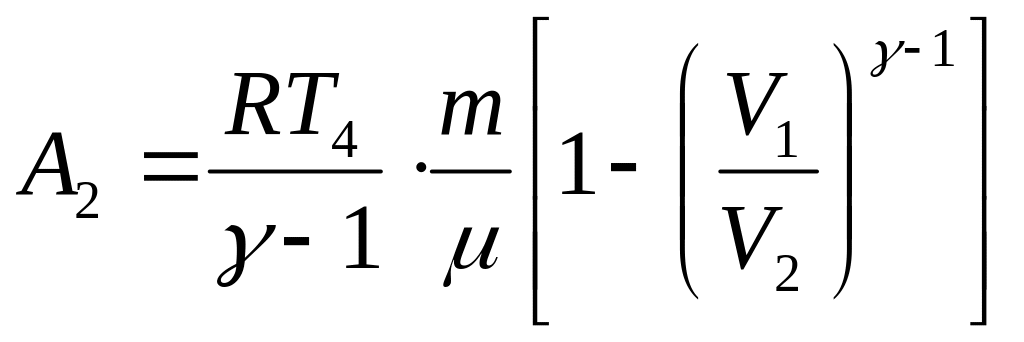 ,
,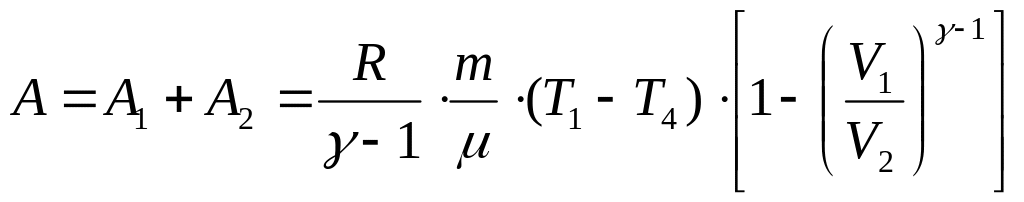 (1)
(1)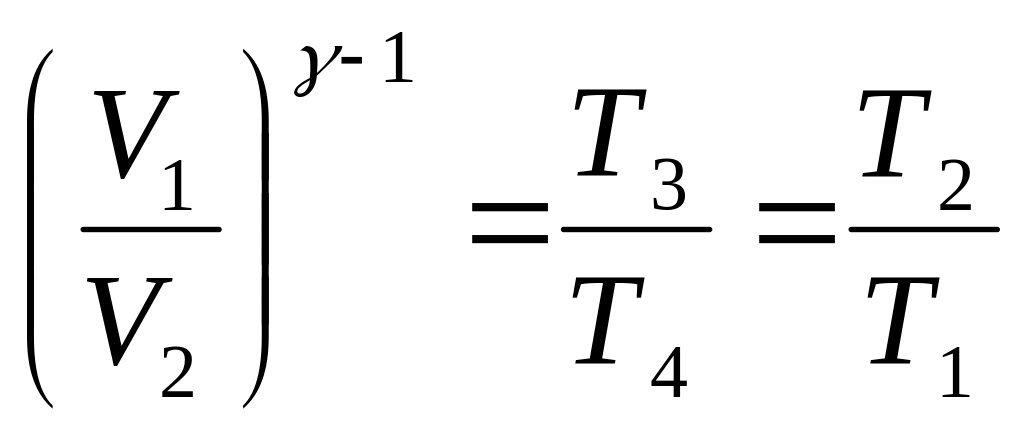 .
(2)
.
(2)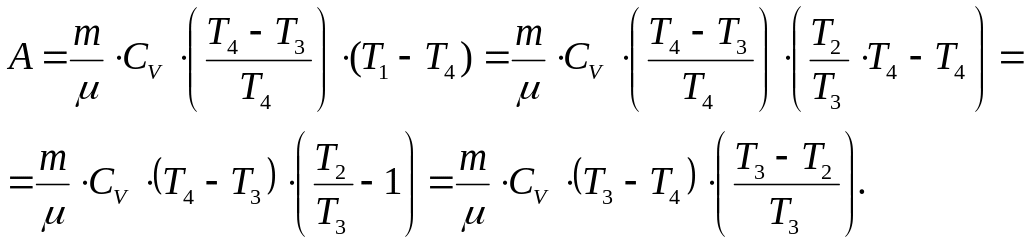
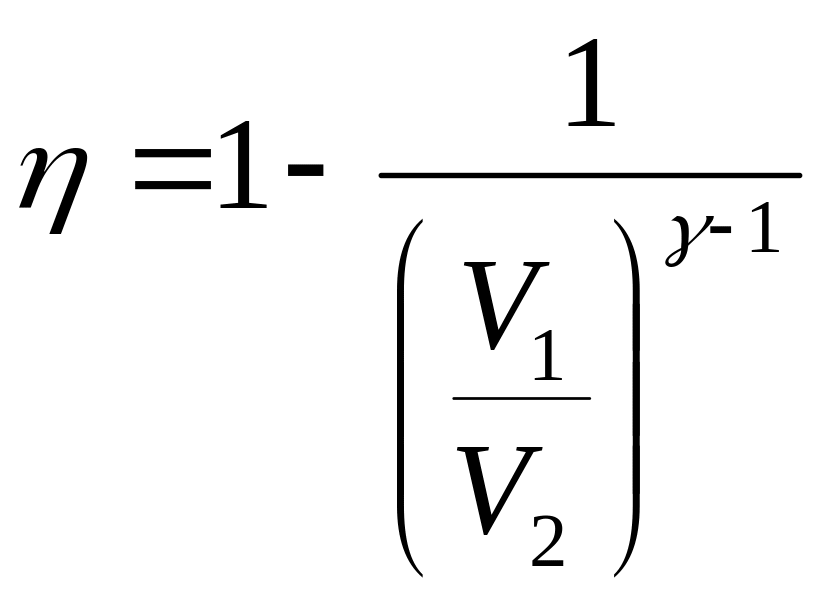 .
. Рис.2.
Рис.2. Рис.1.
Рис.1.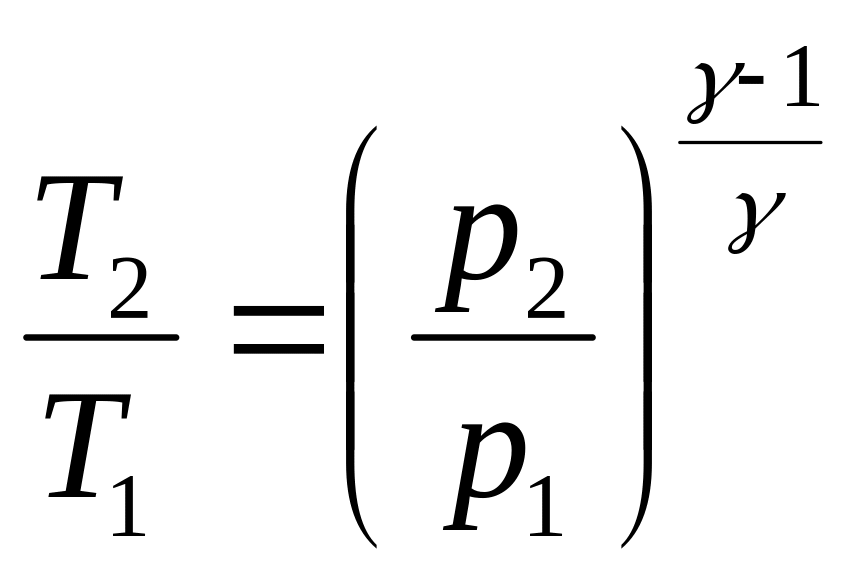 ,
,
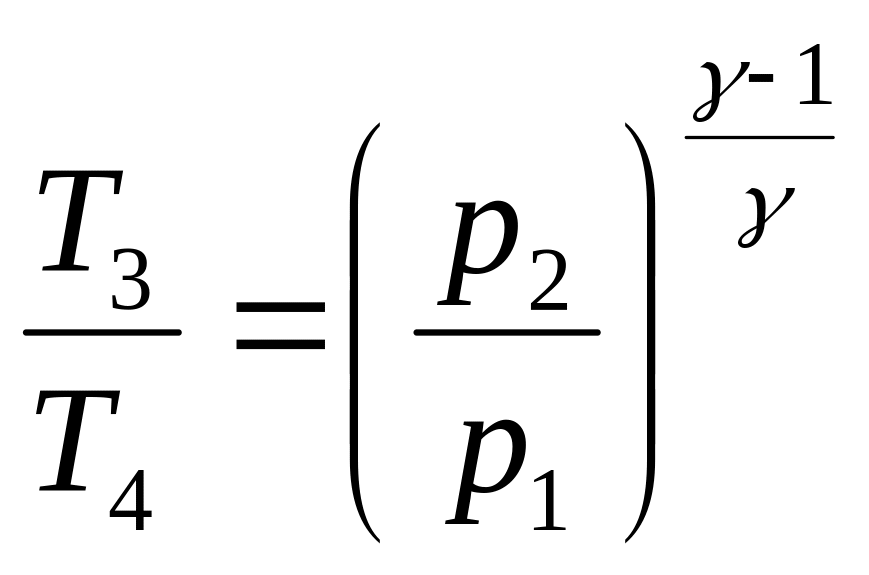 ,
,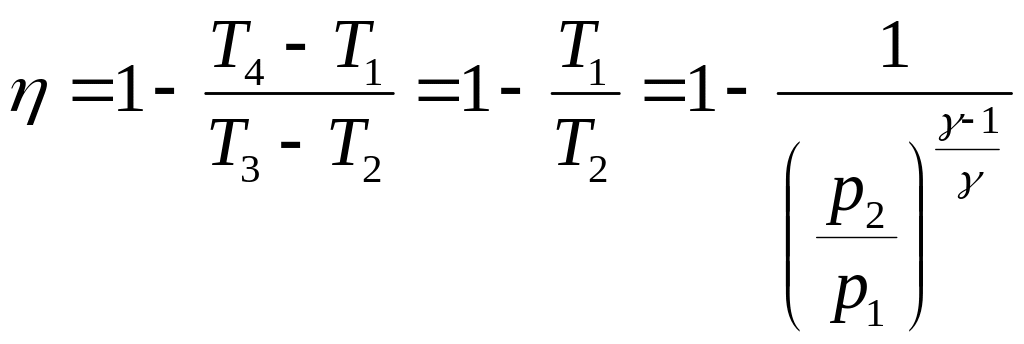 .
.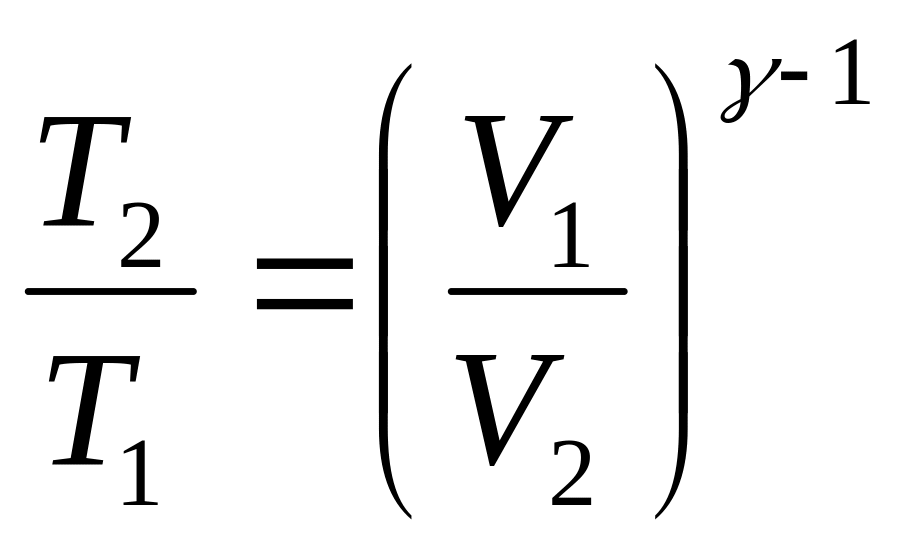 ,
,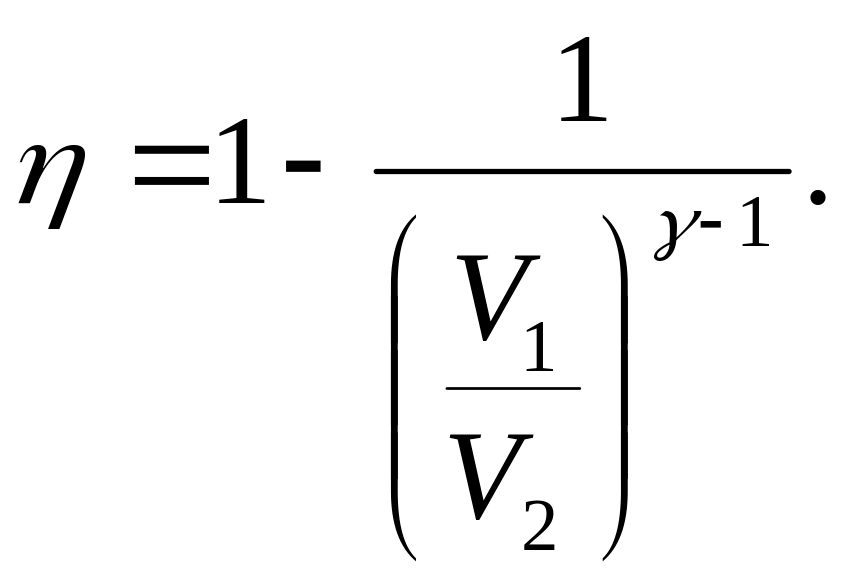
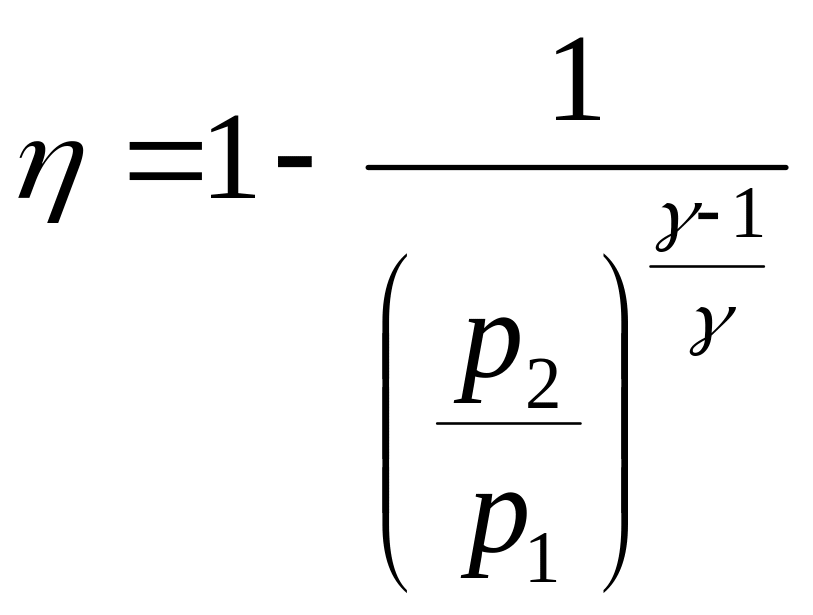 .
.