
2. Молекулярная физика
2.1. С помощью
барометрической формулы определить
давление на высотах 1 км, 10 км, 22 км, считая
![]() Определить высоту над уровнем моря,
если барометр показывает
Определить высоту над уровнем моря,
если барометр показывает
![]()
Дано: |
СИ: |
Решение: |
|
|
Величину атмосферного давления на заданной высоте можно вычислить по барометрической формуле:
где
– высота над уровнем моря, |
|
||
Преобразовав формулу (1), получим зависимость высоты от давления на данной высоте:
|
||
Ответ:
|
||
2.2. Определить
плотность воздуха на высоте 10 км над
уровнем моря при температуре
![]() .
.
Дано: |
СИ: |
Решение: |
|
|
Согласно барометрической формуле:
|
|
||
По уравнению
состояния идеального газа в виде
а так как
Т.о., барометрическую формулу представим в виде:
Плотность воздуха
на уровне моря
Тогда:
Следует заметить, что с подъемом молярная масса воздуха меняется, мы же не учитывали этого и подставляли при вычислениях молярную массу воздуха, рассчитанную вблизи поверхности земли. Поэтому получившийся результат можно считать лишь оценочным, но не точным. |
||
Ответ:
|
||
2.3. При температуре
![]() давление воздуха в шасси самолета.
давление воздуха в шасси самолета.
![]() Найти давление в шасси во время движения
самолета по полосе разгона, если
температура воздуха в нем повысится до
Найти давление в шасси во время движения
самолета по полосе разгона, если
температура воздуха в нем повысится до
![]() .
Изменением объема шины пренебречь.
.
Изменением объема шины пренебречь.
Дано: |
СИ: |
Решение: |
|
|
Так как
то процесс подчиняется закону Шарля:
|
|
||
где
отсюда:
|
||
Ответ:
|
||
2.4. Найти молярную
массу горючей смеси, содержащей кислород
массой
![]() и водород массой
и водород массой
![]() .
.
Дано: |
СИ: |
Решение: |
|
|
Молярная масса смеси – есть отношение массы смеси к количеству вещества смеси:
|
|
||
Масса смеси равна
сумме масс компонентов смеси:
Количество вещества, соответственно равно:
Т.о. молярная масса смеси равна:
|
||
Ответ:
|
||
2.5. Вблизи поверхности
Земли 78.1% массы воздуха приходится на
долю азота, 20.95% – на долю кислорода,
0.94% – на долю аргона. Полагая давление
воздуха
![]() ,
найти парциальное давление азота,
кислорода и аргона. Определить среднюю
молекулярную массу воздуха.
,
найти парциальное давление азота,
кислорода и аргона. Определить среднюю
молекулярную массу воздуха.
Дано: |
СИ: |
Решение: |
|
|
Предположим, что
мы имеем массу воздуха
Воспользовавшись формулой, полученной в задаче (1.7), получим: |
|
||
Пусть данные газы занимают объем , тогда согласно уравнению Менделеева-Клапейрона:
Причем, согласно закону Дальтона, давление равно сумме парциальных давлений компонентов:
Т.о., парциальные давления компонентов воздуха равны соответственно:
|
||
Ответ:
|
||
2.6. Найти молярную массу воздуха, считая, что он состоит по массе из одной части кислорода и трех частей азота.
Дано: |
СИ: |
Решение: |
|
|
Считая воздух идеальным газом, воспользуемся уравнением газового состояния для смеси:
|
|
||
Для смеси справедлив закон Дальтона:
Здесь
Эти величины можно определить из уравнений состояния:
Складывая эти уравнения и используя закон Дальтона, получаем:
Сравнивая это
выражение с (1) и учитывая, что масса
смеси равна:
откуда:
|
||
Ответ:
|
||
2.7. Плотность смеси
азота и водорода при температуре
![]() и давлении
и давлении
![]() равна
равна
![]() .
Найти концентрации молекул азота и
водорода в смеси.
.
Найти концентрации молекул азота и
водорода в смеси.
Дано: |
СИ: |
Решение: |
|
|
Концентрация
однородного по составу газа находится
из уравнения состояния идеального
газа:
откуда
|
|
||
Если
Найдем молярную массу смеси, используя уравнение Менделеева-Клапейрона:
С другой стороны,
можно выразить
При этом учтем, что массу газа можно выразить через его концентрацию:
Т.о.:
Решая в системе уравнения (1) и (2), найдем искомые концентрации:
|
||
Ответ:
|
||
2.8. Нагнетательный
насос засасывает с каждым ходом поршня
![]() воздуха при атмосферном давлении и
температуре
воздуха при атмосферном давлении и
температуре
![]() .
Затем насос подает этот воздух в резервуар
объемом
.
Затем насос подает этот воздух в резервуар
объемом
![]() ,
вначале сообщавшийся с атмосферой.
Сколько качаний должен сделать поршень,
чтобы давление в резервуаре стало равным
4.5 атмосферы при температуре
,
вначале сообщавшийся с атмосферой.
Сколько качаний должен сделать поршень,
чтобы давление в резервуаре стало равным
4.5 атмосферы при температуре
![]() ?
?
Дано: |
СИ: |
Решение: |
|
|
За один ход поршень захватывает порцию воздуха, состояние которого можно описать уравнением:
Перед началом работы насоса термо- |
|
||
динамические
параметры воздуха в резервуаре связаны
соотношением:
По достижении требуемого условия будем иметь:
Тогда количество
качаний можно выразить следующим
образом:
Выразим массы:
|
||
Ответ:
|
||
2.9. Определить
температуру горючей смеси в цилиндре
двигателя внутреннего сгорания в конце
такта сжатия, если давление смеси в
цилиндре до сжатия
![]() ,
в конце сжатия
,
в конце сжатия
![]() ,
температура смеси до сжатия
,
температура смеси до сжатия
![]() ,
степень сжатия
,
степень сжатия
![]() .
.
Дано: |
СИ: |
Решение: |
|
|
Согласно уравнению Менделеева-Клапейрона состояние горючей смеси: а) в начале такта сжатия:
|
|
||
б) в конце такта
сжатия:
откуда:
|
||
Ответ:
|
||
2.10. Горючая смесь
в двигателе Дизеля воспламеняется при
температуре
![]() .
Начальная температура смеси
.
Начальная температура смеси
![]() .
Во сколько раз нужно уменьшить объем
смеси при сжатии, чтобы она воспламенилась?
Сжатие считать адиабатным. Показатель
адиабаты
.
Во сколько раз нужно уменьшить объем
смеси при сжатии, чтобы она воспламенилась?
Сжатие считать адиабатным. Показатель
адиабаты
![]() принять равным 1.4.
принять равным 1.4.
Дано: |
СИ: |
Решение: |
|
|
Т.к. процесс
сжатия можно считать адиабатным, имеет
место уравнение Пуассона
или
|
|
||
С учетом (1) получаем:
или
|
||
Ответ:
|
||
2.11. Чтобы заставить
всплыть подводную лодку, заполненные
водой цистерны лодки продувают сжатым
воздухом. Продувание производится на
глубине
![]() ,
причем воздух принимает температуру
окружающей воды
,
причем воздух принимает температуру
окружающей воды
![]() .
Какое количество воды можно выгнать из
цистерн, выпустив воздух из баллона
емкостью
.
Какое количество воды можно выгнать из
цистерн, выпустив воздух из баллона
емкостью
![]() ,
если давление воздуха в баллоне при
,
если давление воздуха в баллоне при
![]() равно
равно
![]() ,
а плотность морской воды
,
а плотность морской воды
![]() ?
?
Дано: |
СИ: |
Решение: |
|
|
Состояние воздуха в баллоне описывается уравнением:
В
результате расширения воздух вытеснит
объем воды, равный
|
|
||
Давление на глубине , с учетом атмосферного давления, равно:
|
||
Ответ:
|
||
2.12. Баллон, содержащий
![]() азота, при испытании взорвался при
температуре
азота, при испытании взорвался при
температуре
![]() .
Какое количество водорода (в граммах)
можно хранить в этом баллоне при
,
имея пятикратный запас прочности?
Считать прочность баллона не зависящей
от температуры.
.
Какое количество водорода (в граммах)
можно хранить в этом баллоне при
,
имея пятикратный запас прочности?
Считать прочность баллона не зависящей
от температуры.
Дано: |
СИ: |
Решение: |
|
|
Воспользовавшись уравнением Менделеева-Клапейрона, найдем давление, при котором баллон взорвался:
Учитывая, что необходимо иметь запас прочности, давление в бал- |
|
||
лоне должно
составлять величину не более
Поскольку объем баллона не меняется, то:
Откуда масса газа, которую можно безопасно хранить в данном баллоне, равна:
|
||
Ответ:
|
||
2.13. Найти вес
![]() влажного воздуха при температуре
влажного воздуха при температуре
![]() ,
относительной влажности
,
относительной влажности
![]() и нормальном атмосферном давлении.
и нормальном атмосферном давлении.
Дано: |
СИ: |
Решение: |
|
|
В инерциальной системе отсчета вес воздуха будет равен:
Массу воздуха найдем, используя уравнение Менделеева-Клапейрона: |
|
||
Относительная влажность воздуха вычисляется по формуле:
откуда:
Следовательно: При указанной температуре и нормальном атмосферном давлении давление насыщенного пара равно:
|
||
Ответ:
|
||
2.14. В контейнере
высотной ракеты вначале было давление
![]() .
Во сколько раз увеличилось температура
внутри ракеты при ее взлете, если
установленный в контейнере ртутный
барометр стал показывать
.
Во сколько раз увеличилось температура
внутри ракеты при ее взлете, если
установленный в контейнере ртутный
барометр стал показывать
![]() ?
Ракета взлетает вертикально с постоянным
ускорением
?
Ракета взлетает вертикально с постоянным
ускорением
![]() .
.
Дано: |
СИ: |
Решение: |
|
|
В покоящейся ракете высота столбика ртути в барометре определяется условием:
В
ракете, взлетающей вверх с ускорением
|
|
||
него сил должна:
равняться
Масса столбика ртути равна:
Т.к. по условию задачи ракета взлетает с ускорением , то
или
Считая объем контейнера постоянным, запишем закон Шарля:
|
||
Ответ:
|
||
2.15. Сколько времени
надо откачивать газ из сосуда объемом
![]() ротационным масляным насосом, чтобы
давление понизилось от атмосферного
до
ротационным масляным насосом, чтобы
давление понизилось от атмосферного
до
![]() ?
Быстроту действия насоса для указанного
интервала давлений считать постоянной
и равной
?
Быстроту действия насоса для указанного
интервала давлений считать постоянной
и равной
![]() .
Изменением температуры газа в сосуде
во время откачки пренебречь.
.
Изменением температуры газа в сосуде
во время откачки пренебречь.
Дано: |
СИ: |
Решение: |
|
|
Быстрота действия
насоса
|
|
||
Если за время
Согласно условию откачка протекает изотермически, следовательно, подчиняется закону Бойля-Мариотта.
Отбросив величину
Разделив обе
части на приращение времени
и учитывая соотношение (1), имеем:
Разделив переменные
в этом дифференциальном уравнении, и
учитывая, что при изменении времени
от 0 до
Интегрируя, получим:
При нахождении отношения давлений переводить их в систему СИ нет необходимости. |
||
Ответ:
|
||
2.16. Согласно
складским документам манометр на баллоне
с кислородом показывал давление
![]() в помещении с температурой
в помещении с температурой
![]() .
Когда баллон доставили к месту
эксплуатации, манометр показал давление
.
Когда баллон доставили к месту
эксплуатации, манометр показал давление
![]() при температуре
при температуре
![]() .
Определить, произошла ли утечка газа
из баллона при транспортировке.
.
Определить, произошла ли утечка газа
из баллона при транспортировке.
Дано: |
СИ: |
Решение: |
|
|
Пренебрегая изменением объема баллона при изменении температуры, можем считать, что объем постоянен,
т.е.
Согласно уравнению Менделеева-Клапейрона:
|
|
||
Приравнивая объемы, получим:
Т.о., можно считать, что утечки не произошло. |
||
Ответ:
|
||

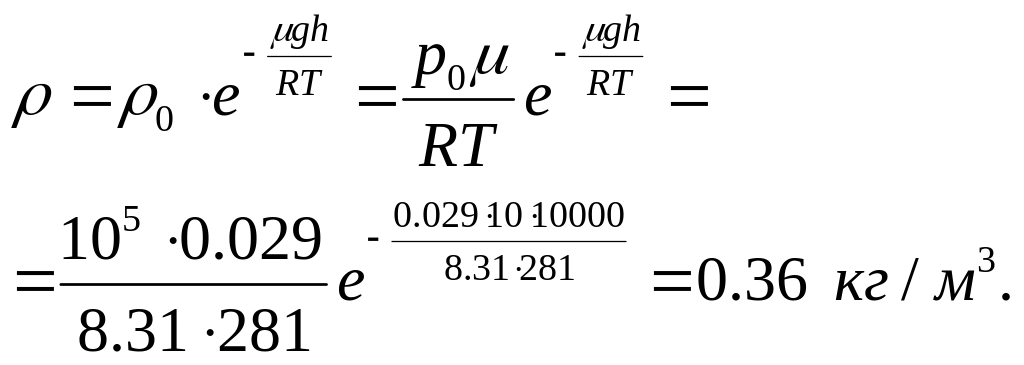
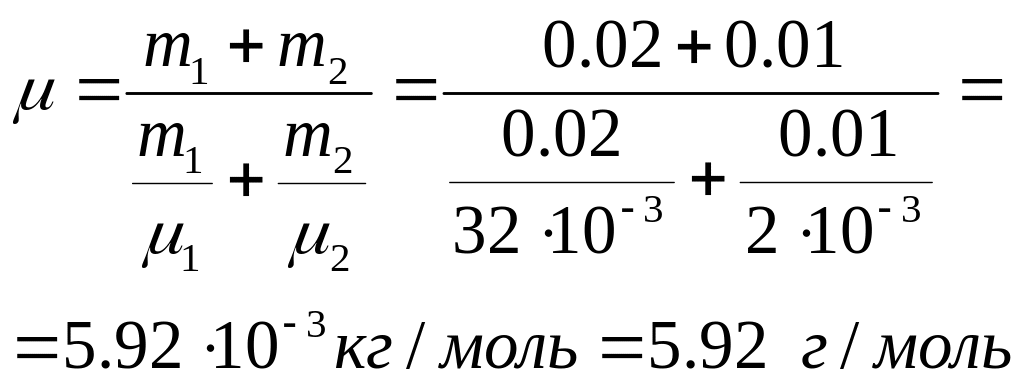
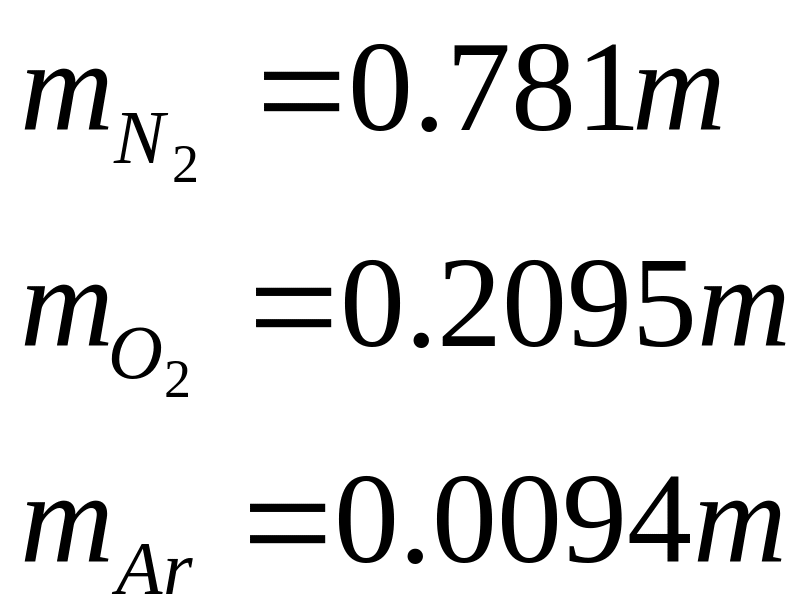
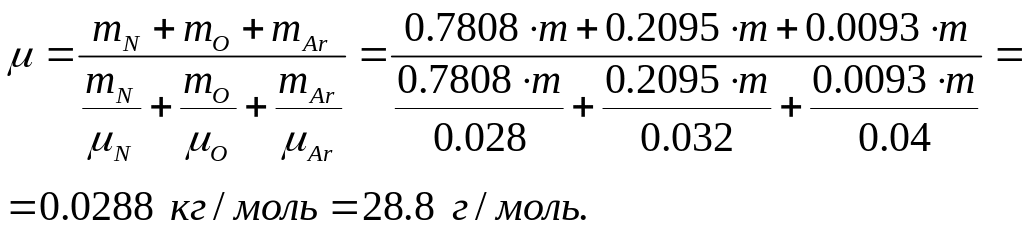
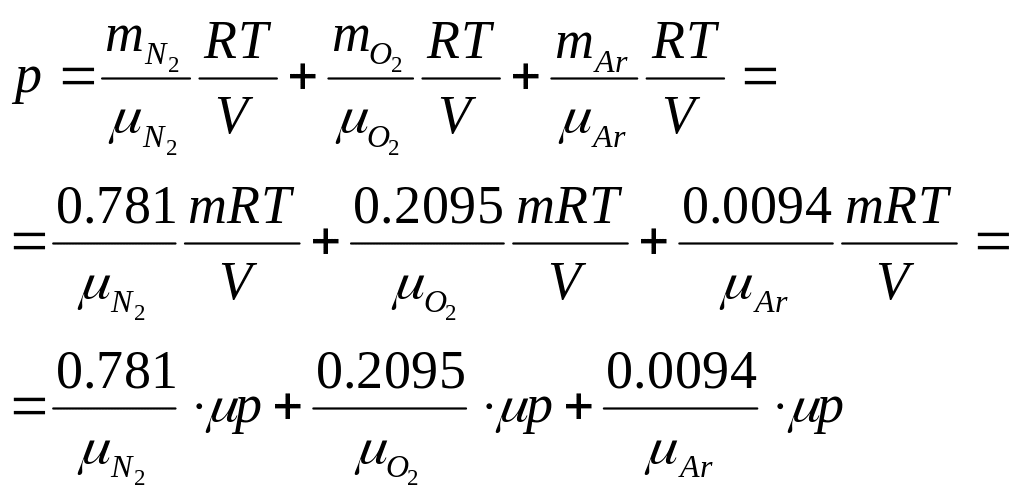

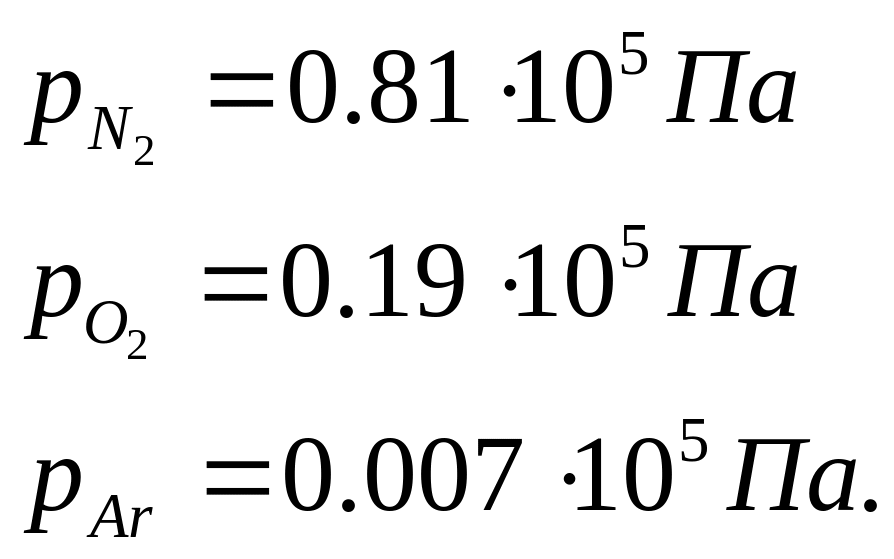
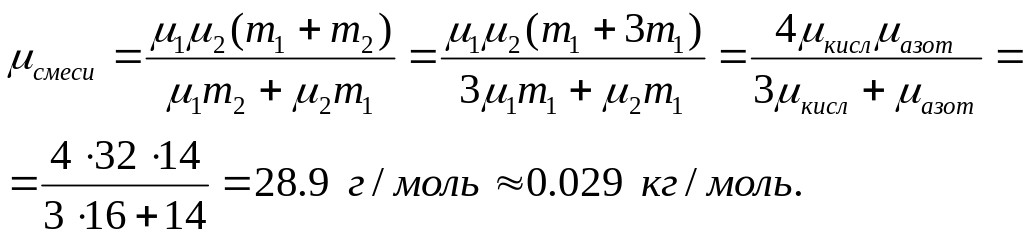
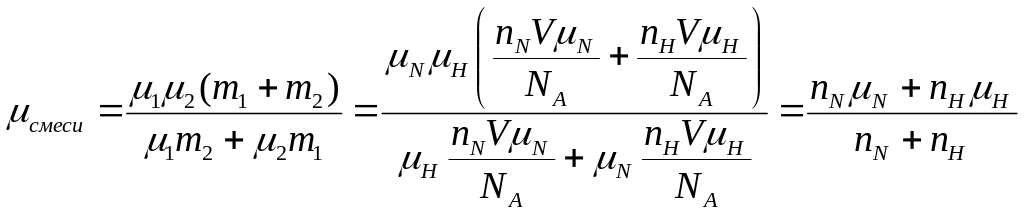 .
.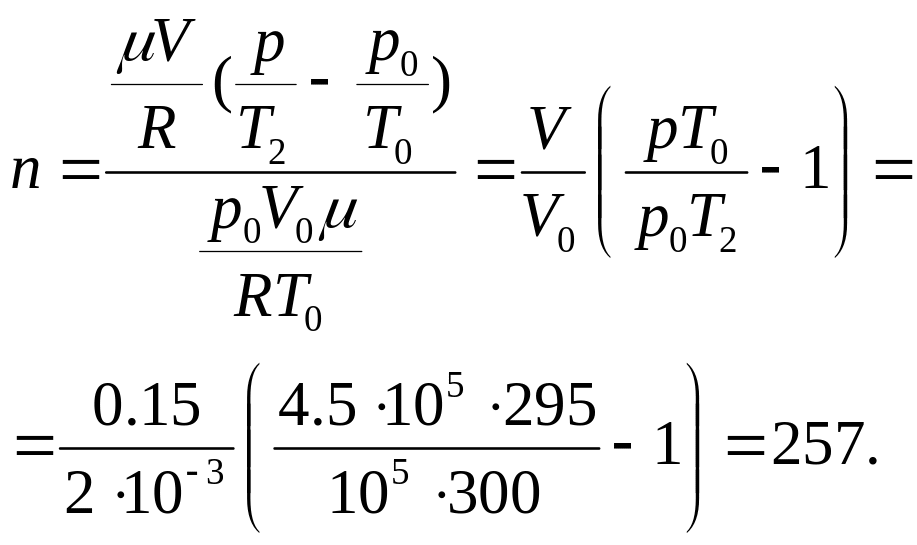
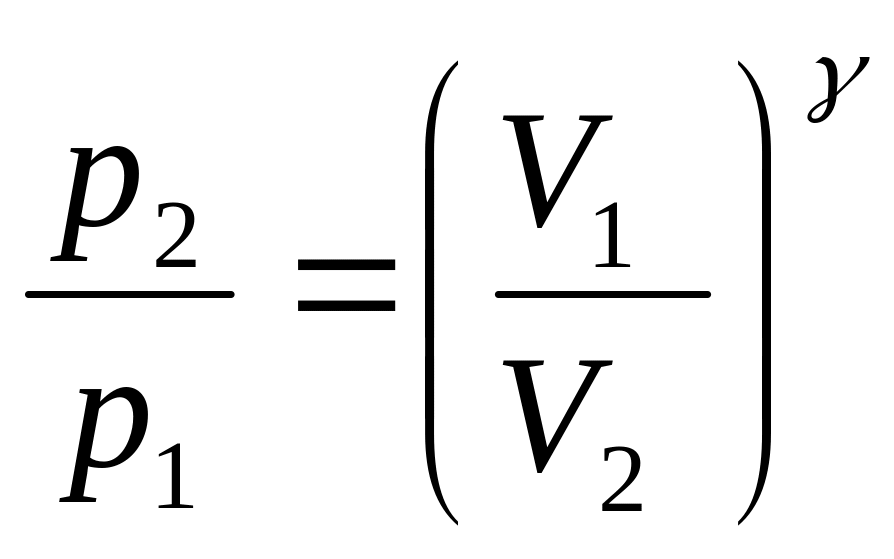 (1)
(1)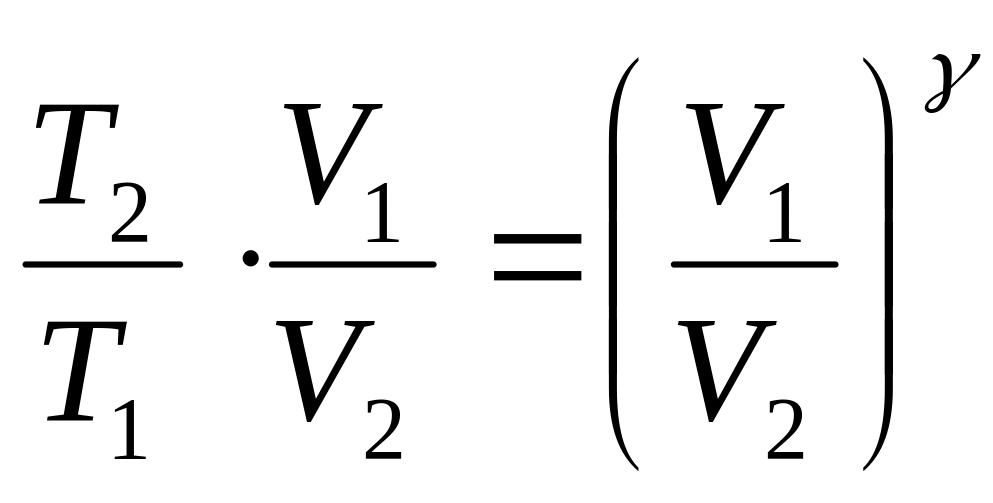
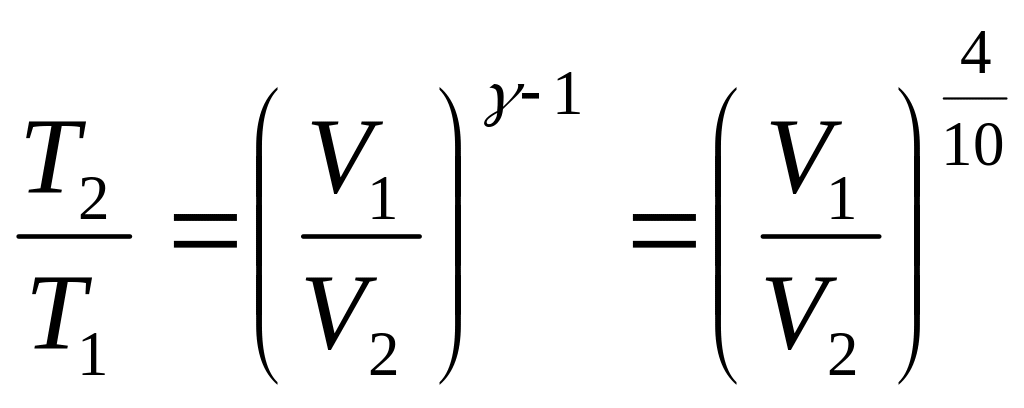
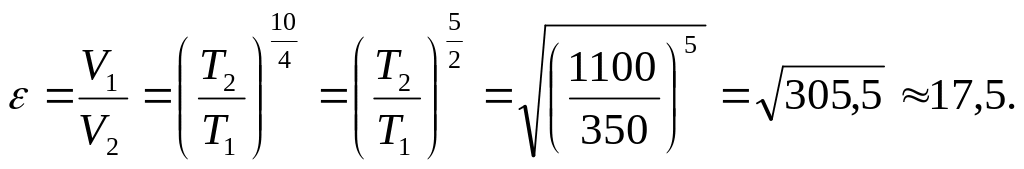
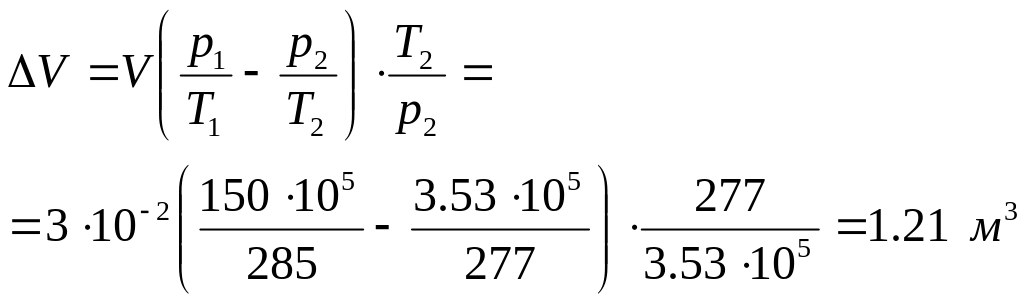
 .
.