
- •А.П. Бырдин н.В. Заварзин а.А. Сидоренко л.П. Цуканова
- •А.П. Бырдин н.В. Заварзин а.А. Сидоренко л.П. Цуканова
- •Введение
- •1. Ортогональные системы функций и обобщенные ряды Фурье. Интегралы Фурье
- •1.1. Исторические замечания
- •1.2. Гильбертово пространство. Ряды Фурье в гильбертовом пространстве
- •1.3. Тригонометрические ряды Фурье
- •1.4. Интегральная формула Фурье. Интеграл Фурье
- •1.5. Условия представимости функции интегралом Фурье
- •1.6. Комплексная форма интеграла Фурье. Преобразование Фурье
- •Преобразование Лапласа и его приложения
- •1.1. Свойства преобразования Лапласа
- •2.2. Решение дифференциальных уравнений операционным методом
- •Импульсные функции и их приложение к решению дифференциальных уравнений
- •Приложение операционного метода к решению систем линейных дифференциальных уравнений с постоянными коэффициентами
- •2.5. Индивидуальные задания
- •Ответы к индивидуальным заданиям
- •Задачи механики и физики, приводящие к основным уравнениям математической физики
- •3.1. Понятие уравнения в частных производных и его решения. Основные уравнения математической физики. Уравнения современной математической физики
- •3.2. Уравнения Пуассона и Лапласа. Вывод уравнений для потенциала электрического поля
- •3.3. Получение уравнения Гельмгольца из уравнений электромагнитного поля
- •3.4. Уравнение распространения тепла в изотропном твердом теле
- •3.5. Уравнение колебаний струны
- •4. Решение одномерных уравнений математической физики. Задача Коши и краевые задачи Коши
- •4.1. Распространение тепла в неограниченном стержне. Фундаментальное решение уравнения теплопроводности
- •4.2. Метод Фурье для одномерного уравнения теплопроводности. Распространение тепла в ограниченном стержне
- •4.3. Общее решение волнового уравнения в случае одной пространственной переменной. Решение Даламбера
- •4.4. Задача Коши для одномерного волнового уравнения. Формула Даламбера
- •4.5. Колебания ограниченной струны. Решение методом Фурье
- •5. Метод Фурье для уравнений математической физики в двумерном и трехмерном пространствах
- •5.1. Оператор Лапласа в декартовых и криволинейных координатах. Граничные задачи для уравнений Лапласа и Пуассона
- •5.2. Разделение переменных в уравнении Лапласа в декартовой и сферической системах координат
- •5.3. Определение потенциала электрического поля внутри параллелепипеда
- •5.4. Разделение переменных в уравнении Лапласа в цилиндрических координатах
- •5.5. Задача Дирихле для уравнения Лапласа в круге. Интеграл Пуассона
- •5.6. Распространение тепла в бесконечном цилиндре
- •5.7. Распространение электромагнитных волн в цилиндрическом волноводе
- •Решение уравнения Гельмгольца методом Фурье
- •5.8. Движение электрона в атоме водорода. Квантовый подход
- •6. Элементы теории специальных функций
- •6.1. Недостаточность элементарных функций для решений дифференциальных уравнений. Дифференциальные уравнения, как источник функций
- •6.2. Гипергеометрическое уравнение и функции гипергеометрического типа
- •6.3. Частные случаи гипергеометрической функции: цилиндрические функции Бесселя
- •6.4. Частные случаи гипергеометрической функции: ортогональные полиномы Лежандра
- •7. Функциональные и степенные ряды и их приложения к решению дифференциальных уравнений
- •7.1 Функциональные ряды. Сходимость и равномерная сходимость
- •7.2. Свойства равномерно сходящихся рядов. Признак равномерной сходимости
- •7.3. Степенные ряды. Интервал сходимости, радиус сходимости
- •7.4. Свойства степенных рядов
- •7.5. Арифметические операции и другие действия над степенными рядами
- •7.6. Разложение функций в степенные ряды
- •7.7. Обобщения степенных рядов – интегро – степенные ряды и ряды Вольтерра
- •8. Приближенно-аналитические методы решения дифференциальных уравнений
- •8.1. Необходимость асимптотических методов
- •8.2. Калибровочные функции. Символы порядка
- •8.3. Пример асимптотического разложения. Определение асимптотического ряда
- •8.4. Асимптотические последовательности и асимптотические разложения
- •8.5. Простейшие асимптотические методы решения дифференциальных уравнений
- •8.6. Метод Линдстедта – Пуанкаре
- •1. Ортогональные системы функций .И обобщенные ряды Фурье. Интегралы Фурье……………………………………..... 4
- •2. Преобразование Лапласа и его приложения…………….19
- •2.3. Импульсные функции и их приложение к решению дифференциальных уравнений …………….……….……..…... 38
- •3. Задачи механики и физики, приводящие к основным уравнениям математической физики ……………………......76
- •4. Решение одномерных уравнений математической физики. Задача Коши и краевые задачи ……...……………107
- •5. Метод Фурье для уравнений математической физики в двумерном и трехмерном пространствах .......…………….133
- •6. Элементы теории специальных функций.........................179
- •8. Приближенно-аналитические методы решения дифференциальных уравнений ….........................................221
- •9. Список литературы………………………………………..247
- •394026 Воронеж, Московский просп., 14
2.2. Решение дифференциальных уравнений операционным методом
Рассмотрим линейное обыкновенное дифференциальное уравнение n-го порядка с постоянными коэффициентами
![]()
![]() .
(2.5)
.
(2.5)
![]()
![]() .
(2.6)
.
(2.6)
Если правая часть уравнения (2.5) является оригиналом, то и решение этого уравнения, удовлетворяющее начальным условиям (2.6), также является оригиналом.
На основании теоремы о дифференцировании оригинала построим изображающее уравнение:
![]()
![]() (2.7)
(2.7)
![]() …+
…+
![]() ,
,
где
![]()
![]() .
.
Определив из алгебраического уравнения
(2.7) неизвестное изображение
![]() ,
найдем соответствующий ему оригинал –
решение исходного дифференциального
уравнения (2.5), удовлетворяющее начальным
условиям (2.6).
,
найдем соответствующий ему оригинал –
решение исходного дифференциального
уравнения (2.5), удовлетворяющее начальным
условиям (2.6).
Пример 1. Найти решение
дифференциального уравнения
![]() ,
удовлетворяющее начальным условиям
,
удовлетворяющее начальным условиям
![]() ,
,
![]() .
.
Решение. Пусть
![]() .
По теореме 6 предыдущего раздела и
таблице изображений получим изображающее
уравнение
.
По теореме 6 предыдущего раздела и
таблице изображений получим изображающее
уравнение
![]()
Подставляя начальные данные, имеем
![]()
Отсюда находим
![]() .
.
Разложим дробь
![]() на сумму простейших дробей
на сумму простейших дробей
![]()
и получим
систему уравнений для определения
коэффициентов
![]() и
и
![]()
![]()
Отсюда находим
![]() ,
,
![]() Таким образом, имеем
Таким образом, имеем
![]() .
.
По
таблице изображений находим решение
уравнения в пространстве оригиналов
![]()
Заметим, что для получения оригинала
из таблицы изображений в рассмотренном
примере, мы применяли прием разложения
правильной дроби на сумму простейших
дробей совершенно так же, как это делается
в интегральном исчислении при
интегрировании дробно-рациональных
функций. Рассмотренный пример показывает,
как находить частное решение
дифференциального уравнения,
удовлетворяющее заданным начальным
условиям. Отыскание решения уравнения
(2.5) по его изображению не лишает
возможности находить и общее решение.
Для этого достаточно считать начальные
значения функции
![]() и ее производных в (2.6) произвольными
постоянными.
и ее производных в (2.6) произвольными
постоянными.
Пример 2. Найти общее решение уравнения
![]() .
.
Решение. По таблице изображений находим
![]() .
.
Полагая , имеем
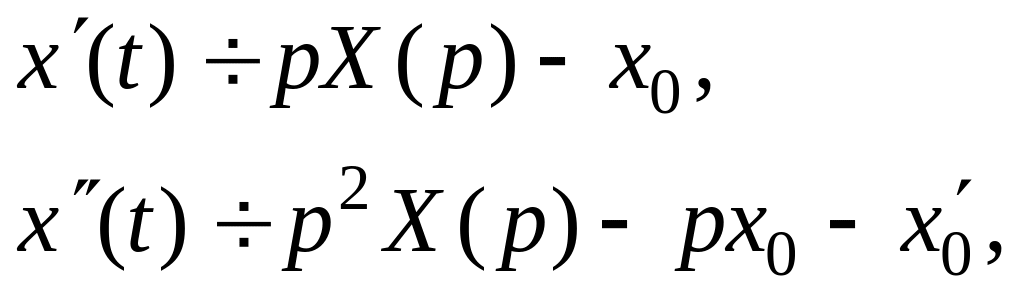
где числа
![]() и
и
![]() играют роль произвольных постоянных.
играют роль произвольных постоянных.
Изображающее уравнение имеет вид
![]() .
.
Отсюда
![]() .
.
Преобразуем первое слагаемое для и найдем по таблице соответствующий ему оригинал
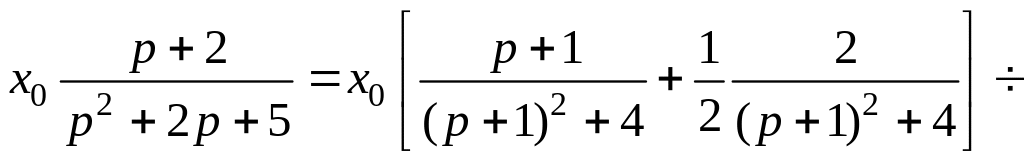
![]()
Для второго слагаемого имеем
![]()
Для отыскания оригинала последнего слагаемого разложим его на простейшие дроби
![]() .
.
Система уравнений для определения коэффициентов разложения имеет вид
![]()
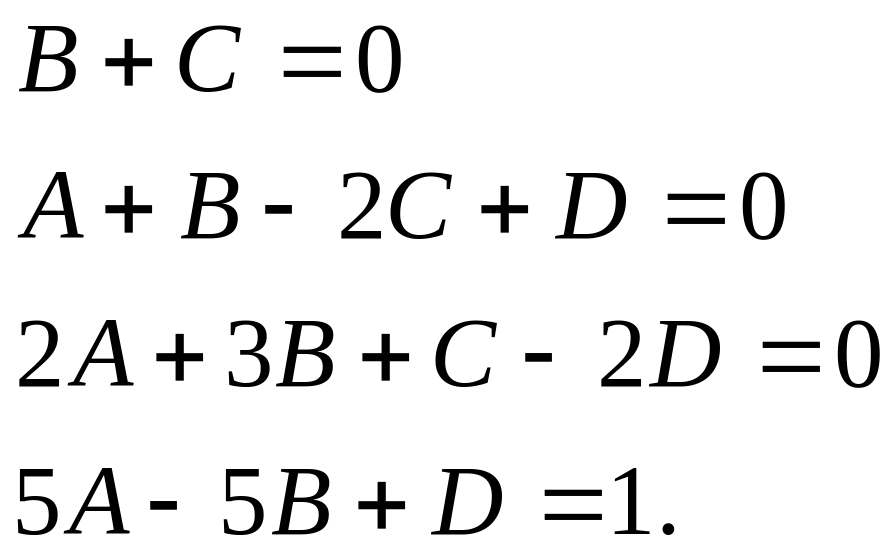
Откуда находим
![]() ,
,
![]() ,
,
![]() .
Следовательно,
.
Следовательно,
![]()
![]()
Собирая оригиналы всех слагаемых, находим решение уравнения
![]() .
.
Положим
![]() ,
,
![]() ,
получим
,
получим
![]()
Если требуется проинтегрировать уравнение (2.5) с нулевыми начальными условиями при
![]() ,
(2.8)
,
(2.8)
то удобно поступить следующим образом:
1) решить операционным методом вспомогательное уравнение
![]() (2.9)
(2.9)
с нулевыми
начальными условиями (2.8) для функции
![]() ;
;
2) воспользоваться для получения решения уравнения (2.5) при условиях (2.8) формулой Дюамеля
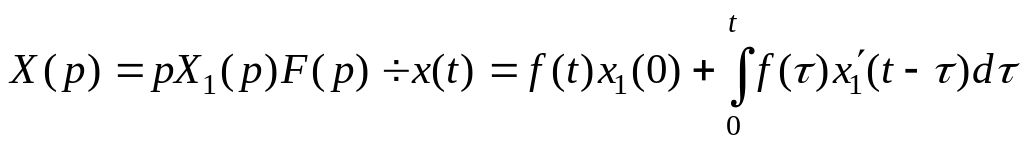 .
(2.10)
.
(2.10)
Пример 3. Решить дифференциальное уравнение
![]() ,
,
![]() .
.
Решение. Составляем вспомогательное уравнение (2.9)
![]() ,
,
![]() .
.
И решаем его операционным методом:
![]() ,
,
![]() .
.
Разлагаем
![]() на простейшие дроби
на простейшие дроби
![]() .
.
Получаем систему уравнений, определяющую коэффициенты разложения
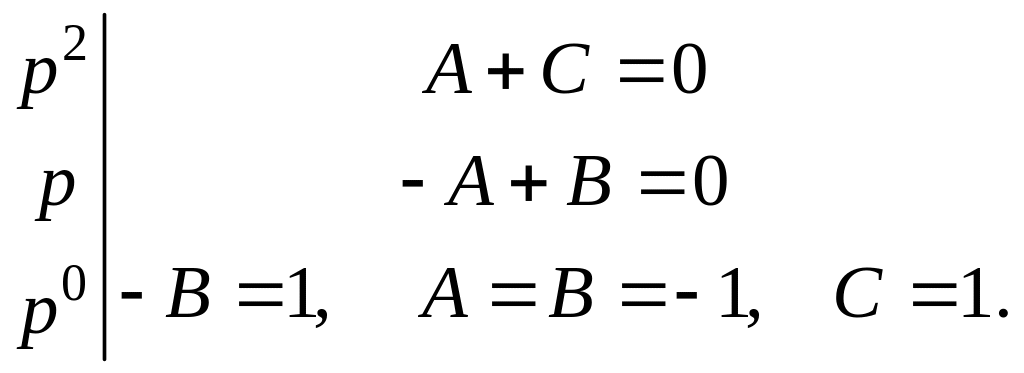
Подставим найденные коэффициенты в выражение и перейдем к оригиналам
![]() ,
,
![]() .
.
Решение заданного уравнения найдем по
формуле Дюамеля (2.10) с учетом того, что
![]() .
Имеем
.
Имеем
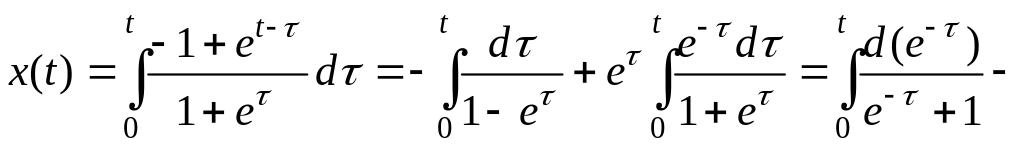
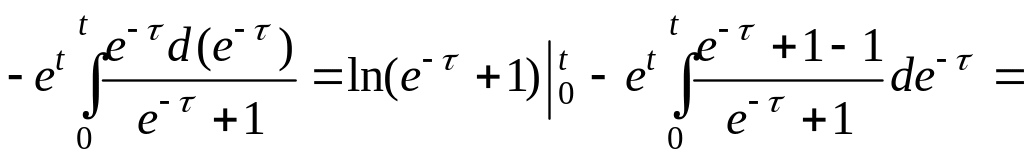

![]() ,
,
![]() .
.
Пример 4. Рассмотрим включение
синусоидальной ЭДС
![]() в контур, состоящий из индуктивности
в контур, состоящий из индуктивности
![]() и сопротивления
и сопротивления
![]() (рис.2).
(рис.2).
L

Д
r






![]() в цепи отсутствовал. Напряжение в цепи,
вызванное включением ЭДС состоит из
суммы напряжения на индуктивности
в цепи отсутствовал. Напряжение в цепи,
вызванное включением ЭДС состоит из
суммы напряжения на индуктивности
![]() и напряжения на сопротивлении
и напряжения на сопротивлении
![]() .
.
Рис.2 Приравняв сумму напряжений в цепи электродвижущей силе получаем дифференциальное уравнение для тока в цепи
![]() ,
,
![]() .
.
Решение уравнения. Построим уравнение для изображений
![]() .
.
из которого находим
изображение тока в цепи
![]()
![]() .
.
Для нахождения оригинала
![]() разложим дробно-рациональную функцию
в правой части последнего равенства на
сумму простейших дробей, используя
метод неопределенных коэффициентов.
Имеем,
разложим дробно-рациональную функцию
в правой части последнего равенства на
сумму простейших дробей, используя
метод неопределенных коэффициентов.
Имеем,
![]() .
.
Система уравнений, определяющая числа A, B, C имеет вид
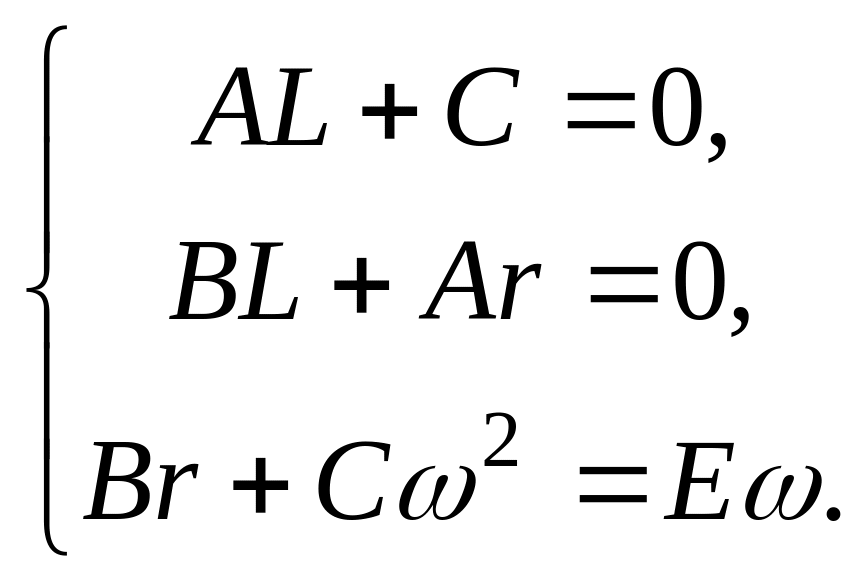
Решая эту систему уравнений, получим коэффициенты разложения
![]() ,
,
![]() ,
,
![]() .
.
Изображение тока теперь принимает вид
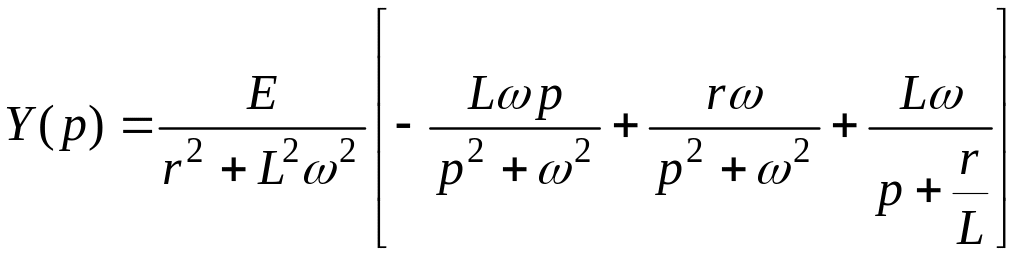 .
.
Перейдем по таблице изображений к оригиналам. Получим
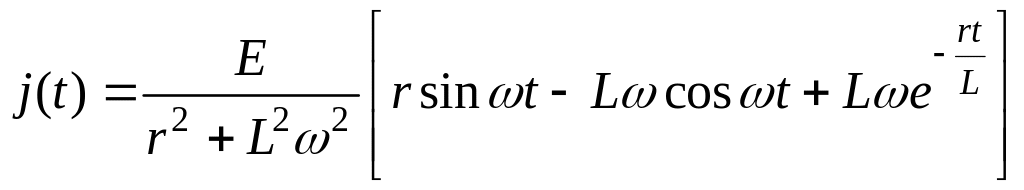 .
.
