1.1. Свойства преобразования Лапласа

1) Линейность. Пусть , ( , где - показатель роста функции . Тогда изображением линейной комбинации этих функций – постоянные, является такая же линейная комбинация изображений:

.

Здесь символом обозначено наибольшее из чисел .

2) Теорема подобия. Пусть , . Тогда при любом постоянном справедливо соотношение

для .

Таким образом, умножение аргумента оригинала на положительное число приводит к делению аргумента изображения на это число.

Пример 2. Зная изображение оригинала , найти изображение оригинала .

Решение. По теореме подобия ^.

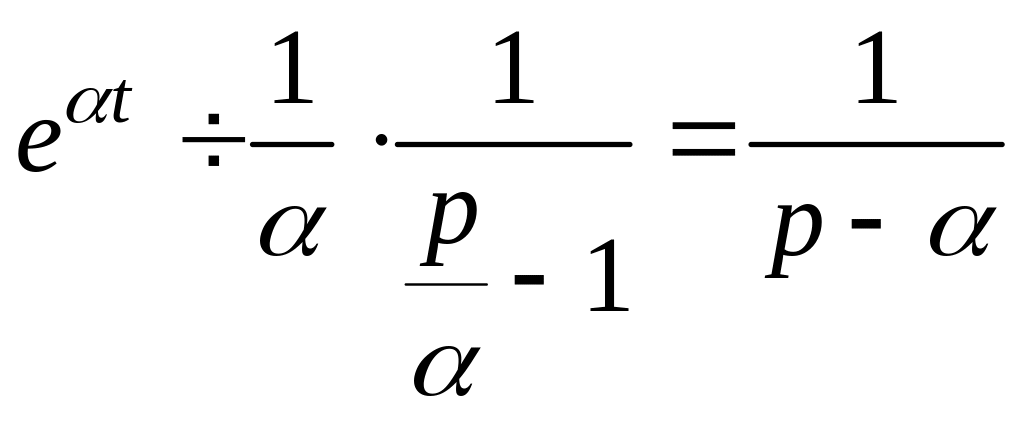3) Теорема запаздывания. Пусть для и пусть

при .

Тогда , т.е. включение оригинала с запаздыванием на равносильно умножению изображения на .

Пример 3. Найти изображение функции

где - функция Хевисайда.

Решение. Воспользовавшись таблицей изображений и теоремой запаздывания, имеем

, .

Таким образом, получим искомое изображение

Замечание к теореме запаздывания.

Соглашение о равенстве нулю функции для здесь особенно важно. При аргумент отрицателен, поэтому =0. График функции получается из графика функции смещением вправо на расстояние , если , и дополнением графика в интервале между 0 и τ отрезком оси .

Следует иметь в виду, что если в формулировке теоремы запаздывания параметр , то формула для изображения теряет силу, а имеет место утверждение.

Вторая теорема запаздывания.

Пусть для и пусть

Тогда .

4) Теорема смещения. Если функция - оригинал имеет изображение для , то при любом вещественном или комплексном оригиналом будет и функция и справедливо соотношение

для .

Пример 4. Найти изображение функции .

Решение. Воспользовавшись результатом примера 1 и теоремой подобия, имеем

Далее используем теорему смещения:

5) Теорема о дифференцировании изображения.

Если функция – оригинал имеет изображение для , то функция также является оригиналом и справедливо соотношение

для .

Пример 5. Используя изображение единичной функции и теорему о дифференцировании изображения найти изображение оригинала = .

Решение. По теореме 5 имеем

.

6) Теорема о дифференцировании оригинала.

Пусть оригинал дифференцируемая функция и его производная также является оригиналом, причем , при . Пусть и . Тогда

= (2.3)

для , где

Следствие. Если удовлетворяют условиям существования изображения при и , то имеют место формулы

…………………………………………………. (2.4)

Это правило является очень важным для практических приложений и выражает примечательное обстоятельство: дифференцирование оригиналов заменяется для изображений элементарным действием – умножением изображения на степень аргумента р с добавлением многочлена, коэффициентами которого являются «начальные значения» оригинала.

Важно то, что в формулы (2.4) входят предельные значения функций . Например, если единичную функцию определить формулой

отличающейся от задания в форме (2.2) значением при , то для обоих случаев при , а следовательно, и изображение равно нулю . Поскольку , то из теоремы 6 имеем

=

Это равенство выполняется только при . Если бы в формуле (2.3) было записано вместо , то это привело бы к ошибке - !

Пример 6. Найти изображение оригинала .

Решение. Обозначим . По теореме 6 имеем

Но .

По таблице изображений . Следовательно,

,

откуда .

7) Теорема интегрирования оригинала.

Интегрирование оригинала от нуля до переменной точки t соответствует в пространстве изображений деление изображения на p:

.

Пример 7. Найти изображение оригинала

Решение. По таблице изображений . По теореме 5 имеем: Используя теорему 7, получим окончательно

.

8) Теорема интегрирования изображения.

Если интеграл сходится, то он является изображением функции , где .

Пример 8. Найти изображение оригинала

Решение. По таблице изображений . По теореме смещения . Использование теоремы 8 дает

=

= .

Выражение называется сверткой функции и и обозначается

9) Теорема о свертке.

Изображение свертки оригиналов равно произведению их изображений

для где для и для .

Пример 9. Найти изображение оригинала .

Решение. По таблице изображений , . По теореме 9 имеем .

В таблице 1 собраны формулы соответствия, полученные в настоящем параграфе.

Таблица 1

Номер формулы	Оригинал	Изображение
1	1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17