
- •А.П. Бырдин н.В. Заварзин а.А. Сидоренко л.П. Цуканова
- •А.П. Бырдин н.В. Заварзин а.А. Сидоренко л.П. Цуканова
- •Введение
- •1. Ортогональные системы функций и обобщенные ряды Фурье. Интегралы Фурье
- •1.1. Исторические замечания
- •1.2. Гильбертово пространство. Ряды Фурье в гильбертовом пространстве
- •1.3. Тригонометрические ряды Фурье
- •1.4. Интегральная формула Фурье. Интеграл Фурье
- •1.5. Условия представимости функции интегралом Фурье
- •1.6. Комплексная форма интеграла Фурье. Преобразование Фурье
- •Преобразование Лапласа и его приложения
- •1.1. Свойства преобразования Лапласа
- •2.2. Решение дифференциальных уравнений операционным методом
- •Импульсные функции и их приложение к решению дифференциальных уравнений
- •Приложение операционного метода к решению систем линейных дифференциальных уравнений с постоянными коэффициентами
- •2.5. Индивидуальные задания
- •Ответы к индивидуальным заданиям
- •Задачи механики и физики, приводящие к основным уравнениям математической физики
- •3.1. Понятие уравнения в частных производных и его решения. Основные уравнения математической физики. Уравнения современной математической физики
- •3.2. Уравнения Пуассона и Лапласа. Вывод уравнений для потенциала электрического поля
- •3.3. Получение уравнения Гельмгольца из уравнений электромагнитного поля
- •3.4. Уравнение распространения тепла в изотропном твердом теле
- •3.5. Уравнение колебаний струны
- •4. Решение одномерных уравнений математической физики. Задача Коши и краевые задачи Коши
- •4.1. Распространение тепла в неограниченном стержне. Фундаментальное решение уравнения теплопроводности
- •4.2. Метод Фурье для одномерного уравнения теплопроводности. Распространение тепла в ограниченном стержне
- •4.3. Общее решение волнового уравнения в случае одной пространственной переменной. Решение Даламбера
- •4.4. Задача Коши для одномерного волнового уравнения. Формула Даламбера
- •4.5. Колебания ограниченной струны. Решение методом Фурье
- •5. Метод Фурье для уравнений математической физики в двумерном и трехмерном пространствах
- •5.1. Оператор Лапласа в декартовых и криволинейных координатах. Граничные задачи для уравнений Лапласа и Пуассона
- •5.2. Разделение переменных в уравнении Лапласа в декартовой и сферической системах координат
- •5.3. Определение потенциала электрического поля внутри параллелепипеда
- •5.4. Разделение переменных в уравнении Лапласа в цилиндрических координатах
- •5.5. Задача Дирихле для уравнения Лапласа в круге. Интеграл Пуассона
- •5.6. Распространение тепла в бесконечном цилиндре
- •5.7. Распространение электромагнитных волн в цилиндрическом волноводе
- •Решение уравнения Гельмгольца методом Фурье
- •5.8. Движение электрона в атоме водорода. Квантовый подход
- •6. Элементы теории специальных функций
- •6.1. Недостаточность элементарных функций для решений дифференциальных уравнений. Дифференциальные уравнения, как источник функций
- •6.2. Гипергеометрическое уравнение и функции гипергеометрического типа
- •6.3. Частные случаи гипергеометрической функции: цилиндрические функции Бесселя
- •6.4. Частные случаи гипергеометрической функции: ортогональные полиномы Лежандра
- •7. Функциональные и степенные ряды и их приложения к решению дифференциальных уравнений
- •7.1 Функциональные ряды. Сходимость и равномерная сходимость
- •7.2. Свойства равномерно сходящихся рядов. Признак равномерной сходимости
- •7.3. Степенные ряды. Интервал сходимости, радиус сходимости
- •7.4. Свойства степенных рядов
- •7.5. Арифметические операции и другие действия над степенными рядами
- •7.6. Разложение функций в степенные ряды
- •7.7. Обобщения степенных рядов – интегро – степенные ряды и ряды Вольтерра
- •8. Приближенно-аналитические методы решения дифференциальных уравнений
- •8.1. Необходимость асимптотических методов
- •8.2. Калибровочные функции. Символы порядка
- •8.3. Пример асимптотического разложения. Определение асимптотического ряда
- •8.4. Асимптотические последовательности и асимптотические разложения
- •8.5. Простейшие асимптотические методы решения дифференциальных уравнений
- •8.6. Метод Линдстедта – Пуанкаре
- •1. Ортогональные системы функций .И обобщенные ряды Фурье. Интегралы Фурье……………………………………..... 4
- •2. Преобразование Лапласа и его приложения…………….19
- •2.3. Импульсные функции и их приложение к решению дифференциальных уравнений …………….……….……..…... 38
- •3. Задачи механики и физики, приводящие к основным уравнениям математической физики ……………………......76
- •4. Решение одномерных уравнений математической физики. Задача Коши и краевые задачи ……...……………107
- •5. Метод Фурье для уравнений математической физики в двумерном и трехмерном пространствах .......…………….133
- •6. Элементы теории специальных функций.........................179
- •8. Приближенно-аналитические методы решения дифференциальных уравнений ….........................................221
- •9. Список литературы………………………………………..247
- •394026 Воронеж, Московский просп., 14
5.4. Разделение переменных в уравнении Лапласа в цилиндрических координатах
В цилиндрических координатах
![]() ,
показанных на рис. 9, уравнение Лапласа
принимает вид
,
показанных на рис. 9, уравнение Лапласа
принимает вид
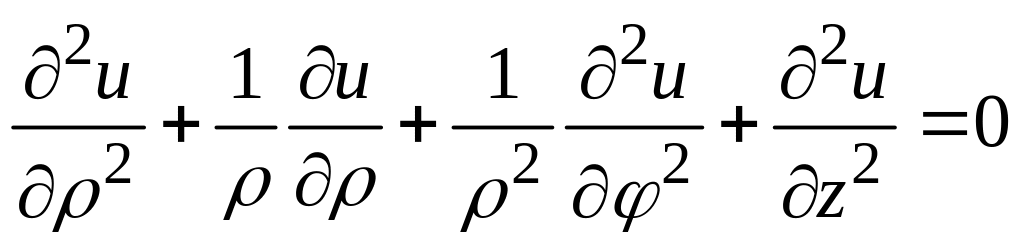 .
(5.45)
.
(5.45)
Для перехода к такой форме лапласиана в цилиндрических координатах нужно в формуле (5.3) преобразовать первый член, выполнив дифференцирование по . Для разделения переменных произведем подстановку в уравнении (5.45)
![]() , (5.46)
, (5.46)
после чего разделим обе части полученного уравнения на произведение функций (5.46). В результате имеем
![]() , (5.47)
, (5.47)
где штрихи над буквами обозначают
производные по соответствующим
аргументам,
![]() – параметр разделения. Параметр
остается произвольным пока не наложены
граничные условия в направлении
– параметр разделения. Параметр
остается произвольным пока не наложены
граничные условия в направлении
![]() .
Основанием для приравнивания выражений
в (5.47) постоянной является тот факт, что
левая часть равенства зависит от
и
,
а правая только от
,
и равенство должно выполняться для
всех значений
.
.
Основанием для приравнивания выражений
в (5.47) постоянной является тот факт, что
левая часть равенства зависит от
и
,
а правая только от
,
и равенство должно выполняться для
всех значений
.
Из соотношений (5.47) вытекают следующие дифференциальные уравнения
![]() ,
(5.48)
,
(5.48)
![]() .
(5.49)
.
(5.49)
Частными решениями уравнения (5.48),
получаемыми с помощью характеристического
уравнения, являются функции
![]() или в действительной форме
или в действительной форме
![]() ,
,
![]() .
.
Для нахождения решения уравнения (5.49),
включающего две неизвестные функции
![]() ,
преобразуем его к виду
,
преобразуем его к виду
![]() ,
(5.50)
,
(5.50)
где
![]() –
постоянная разделения. Основания для
приравнивания отношений константе
такие же что и в случае (5.47).
–
постоянная разделения. Основания для
приравнивания отношений константе
такие же что и в случае (5.47).
Приравнивая каждое отношение в (5.50) постоянной разделения , получим дифференциальные уравнения для функций :
![]() ,
(5.51)
,
(5.51)
 . (5.52)
. (5.52)
Первое из этих уравнений имеет решения
![]() ,
или в действительной форме
,
или в действительной форме
![]() ,
,
![]() .
.
Для того чтобы решение было однозначным, параметр разделения должен быть целым числом.
Если в уравнении (5.52) сделать замену
независимой переменной
![]() ,
то оно принимает вид стандартного
уравнения Бесселя
,
то оно принимает вид стандартного
уравнения Бесселя
 .
(5.53)
.
(5.53)
Его решения для целых значений параметра
– функции Бесселя
![]() и функции Неймана
и функции Неймана
![]() порядка
[11]
порядка
[11]
 ,
,
![]()
![]() .
.
Представление функций Неймана в виде ряда можно найти в математических справочниках. Для приближенных расчетов можно использовать нижеследующие асимптотические выражения для этих функций.
При
![]()


где
![]() – гамма-функция,
– гамма-функция,
![]() – действительное и неотрицательное
число.
– действительное и неотрицательное
число.
При
![]() ,
,
![]() ,
,
![]()
Переход от области «малых» значений
к области больших значений имеет место
при
![]() .
.
5.5. Задача Дирихле для уравнения Лапласа в круге. Интеграл Пуассона
Решение краевых задач для уравнения Лапласа ряда простейших областей (прямоугольник, круг, цилиндр, шар и некоторых других) можно найти методом разделения переменных. В этом разделе рассматривается задача Дирихле, для решения которой используются только элементарные функции.
Для уравнения Лапласа справедливо следующее утверждение.
Теорема. Пусть ограниченная
область Ω пространства имеет кусочно-гладкую
(поверхность Г для трехмерной области
Ω или кривую Г для двумерной области).
Пусть на границе области Г задана
непрерывная функция
![]() (или
(или
![]() ),
если Ω - область плоскости. Тогда
существует на замкнутой области Ώ = Ω +
Г единственная непрерывная функция
(или
),
если Ω - область плоскости. Тогда
существует на замкнутой области Ώ = Ω +
Г единственная непрерывная функция
(или
![]() )
гармоническая на Ω и такая, что
)
гармоническая на Ω и такая, что
![]()
(или
![]() в случае двумерной области Ω).
в случае двумерной области Ω).
Эта задача, как отмечалось в п.5.1,
называемая задачей Дирихле, хорошо
исследована в математической физике.
Известны ее решения в аналитической
форме и различные приближенные методы
решения. Сформулированная выше теорема
имеет простую физическую интерпретацию,
если под функцией
понимать температуры тела в точке
![]() .
Действительно, если на границе Г
тела Ω все время поддерживать температуру
,
равную
,
где
– заданная непрерывная на границе тела
функция, то внутри тела установится
вполне определенная (единственная в
каждой точке тела) температура
.
.
Действительно, если на границе Г
тела Ω все время поддерживать температуру
,
равную
,
где
– заданная непрерывная на границе тела
функция, то внутри тела установится
вполне определенная (единственная в
каждой точке тела) температура
.
Рассмотрим решение задачи Дирихле для
плоской области с частным видом граничного
условия. Пусть на плоскости
имеется круг радиуса
![]() c центром в начале координат
и на его границе – окружности, задана
функция
c центром в начале координат
и на его границе – окружности, задана
функция
![]() ,
где
– полярный угол. Требуется найти функцию
,
где
– полярный угол. Требуется найти функцию
![]() непрерывную в круге и на его границе,
удовлетворяющую внутри круга уравнению
Лапласа.
непрерывную в круге и на его границе,
удовлетворяющую внутри круга уравнению
Лапласа.
Таким образом, уравнения задачи Дирихле имеют вид
,
![]()
![]() Ω , (5.54)
Ω , (5.54)
![]() ,
(5.55)
,
(5.55)
где
![]() – полярные координаты точки, Ω – открытый
круг, Г - ограничивающая область Ω
окружность,
-
заданная на границе функция.
– полярные координаты точки, Ω – открытый
круг, Г - ограничивающая область Ω
окружность,
-
заданная на границе функция.
Из уравнения (5.45) получаем уравнение
для функции
![]() ),
не зависящей от
),
не зависящей от

или
 .
(5.56)
.
(5.56)
Будем решать задачу методом разделения переменных, т.е. будем искать частное решение уравнения (5.56), вида
![]() .
(5.57)
.
(5.57)
Подставляя предполагаемую форму решения (5.57) в уравнение (5.56), получим
![]() .
.
Разделяя переменные, имеем
![]() .
(5.58)
.
(5.58)
Так как левая часть не зависит от , а правая от , то они равны постоянной, которую обозначили . Из равенств (5.58) получаем два дифференциальных уравнения
![]() ,
(5.59)
,
(5.59)
![]() .
(5.60)
.
(5.60)
Уравнение (5.59) является дифференциальным
уравнением с постоянными коэффициентами.
Частное решение его ищем в виде
![]() для
для
![]() .
Подставив эту функцию в уравнение
получим характеристическое уравнение
.
Подставив эту функцию в уравнение
получим характеристическое уравнение
![]() ,
,
![]() .
.
Общее решение уравнения (5.59) является
линейной комбинацией его частных решений
с найденными значениями
![]()
![]() .
.
Поскольку решение должно периодически
зависит от
(для однозначности решения в точках
=0,
2π, …), то число
должно быть целым и при этом можно
ограничиться натуральными значениями
![]() . Заметим, что если бы отношения в (5.58)
приравняли -
,
то не получили бы периодической
зависимости от
.
Таким образом, общее решение уравнения
(5.59) можно записать для
. Заметим, что если бы отношения в (5.58)
приравняли -
,
то не получили бы периодической
зависимости от
.
Таким образом, общее решение уравнения
(5.59) можно записать для
![]() так
так
![]() .
(5.61)
.
(5.61)
Решение уравнения (5.60) будем искать в виде
![]() .
.
Подставим в уравнение (5.60) эту функцию
при
![]() ,
получим
,
получим
![]() ,
,
![]()
т.е.
![]() .
Отсюда для
получим решение
.
Отсюда для
получим решение
![]() .
(5.62)
.
(5.62)
Поскольку решение должно быть конечным
при
![]() (это понятно и из физических соображений),
то
(это понятно и из физических соображений),
то
![]() .
Подставим выражения (5.61) и (5.62) в формулу
(5.57) и учитывая, что
,
получим частное решение уравнения
Лапласа
.
Подставим выражения (5.61) и (5.62) в формулу
(5.57) и учитывая, что
,
получим частное решение уравнения
Лапласа
![]() (
)
(5.63)
(
)
(5.63)
где
![]() и учтена зависимость коэффициентов от
числа
.
и учтена зависимость коэффициентов от
числа
.
Если , то уравнения (5.59) и (5.60) примут вид
![]()
![]() .
.
Первое из них имеет решение вида
![]() (5.64)
(5.64)
и не является периодической функцией
от
если
![]() .
Для однозначности решения необходимо
требование
.
Второе уравнение можно записать так
.
Для однозначности решения необходимо
требование
.
Второе уравнение можно записать так
![]() .
.
Интегрируя, получим
![]() или
или
![]() .
.
Проинтегрировав еще один раз, имеем
![]() .
(5.65)
.
(5.65)
При
![]()
![]() .
Поэтому для ограниченности решения
уравнения (5.65) надо потребовать
.
Поэтому для ограниченности решения
уравнения (5.65) надо потребовать
![]() .
.
Таким образом, для имеется частное решение уравнения Лапласа – константа
![]() (5.66)
(5.66)
где
![]() .
.
Отметим, что частные решения (5.63) и (5.66) удовлетворяют условию конечности при всех значениях из области Ω и условию однозначности, т.е. периодичности по . Однако граничному условию (5.55) эти решения, вообще говоря, не удовлетворяют. Для того чтобы удовлетворить граничному условию (5.55) запишем решение уравнения (5.56) в виде суммы
 .
(5.67)
.
(5.67)
Сумма (5.67) является суммой бесконечного числа членов. Она будет решением уравнения Лапласа с непрерывными частными производными второго порядка по и по (т.е. гармонической функцией) при достаточно хорошей сходимости функционального ряда в (5.67).
Подберем теперь коэффициенты ряда
(5.67) так, чтобы удовлетворялось граничное
условие (5.55). Подставив в (5.67)
![]() ,
на основании условия (5.55) получим
,
на основании условия (5.55) получим
 .
(5.68)
.
(5.68)
Чтобы равенство (5.68) было возможным, нужно, чтобы
функция
разлагалась в ряд Фурье в интервале и
чтобы
![]() и
и
![]() ,
были коэффициентами Фурье этой функции.
Поэтому должны выполняться равенства
,
были коэффициентами Фурье этой функции.
Поэтому должны выполняться равенства

 ,
,
 .
(5.69)
.
(5.69)
Таким образом, получено формальное решение задачи Дирихле (5.54), (5.55) для круга в виде ряда (5.67) с коэффициентами (5.69). Чтобы убедиться в том, что полученная функция действительно является искомым решением, нужно убедиться в сходимости ряда, возможности его почленного дифференцирования, а также доказать непрерывность функции (5.67) на границе круга.
Для этого подставим выражения (5.69) для коэффициентов Фурье в решение (5.67). Получим

Таким образом, имеем
 .
(5.70)
.
(5.70)
Используя формулу Эйлера
![]() ,
,
выражение в квадратных скобках (5.70) можно записать так:
 (5.71)
(5.71)
Здесь использовалась формула для суммы геометрической прогрессии
![]() ,
,
![]() ,
,
при
![]() .
.
Упростим выражение (5.71), приведя к общему знаменателю. Учитывая

и приведенную выше формулу Эйлера, получим окончательный вид решения (5.70)
 .
(5.72)
.
(5.72)
Полученная формула, дающая решение задачи Дирихле внутри круга, называется интегралом Пуассона. Подынтегральное выражение
![]() =
=
называется ядром Пуассона. Отметим,
что
>0
при
![]() .
Анализ интеграла Пуассона показывает
[1], что если функция
непрерывна, то функция
,
определенная формулой (5.72), удовлетворяет
уравнению Лапласа и при
.
Анализ интеграла Пуассона показывает
[1], что если функция
непрерывна, то функция
,
определенная формулой (5.72), удовлетворяет
уравнению Лапласа и при
![]() выполняется
выполняется
![]() .
Таким образом, интеграл Пуассона является
решением задачи Дирихле для круга.
.
Таким образом, интеграл Пуассона является
решением задачи Дирихле для круга.
