3.2. Уравнения Пуассона и Лапласа. Вывод уравнений для потенциала электрического поля
Исторические сведения
Из курса общей физики известно, что между покоящимися электрическими зарядами действует сила, прямо пропорциональна произведению величин этих зарядов и обратно пропорциональна квадрату расстояния между ними. Направлена сила по прямой, соединяющей заряды. Этот эмпирически полученный закон получил обоснование в XVIII веке, в работах 1785-1789 годов выдающегося французского военного инженера и ученного Шарля Огюстена Кулона (1736-1806 г). Правда, несколько раньше, в 1773г. английскому ученному Г. Кавендишу удалось экспериментально показать, что взаимодействие электрических зарядов осуществляется по закону “обратных квадратов”. Однако его работы опубликованы не были.
… … …
Закон Кулона взаимодействия электрических зарядов в современных обозначениях в системе единиц СИ записывается в виде
,
(3.2)
где
-
постоянная, зависящая от выбора единиц
измерения, называемая электрической
постоянной,
- расстояние между зарядами.
В системе СИ
,
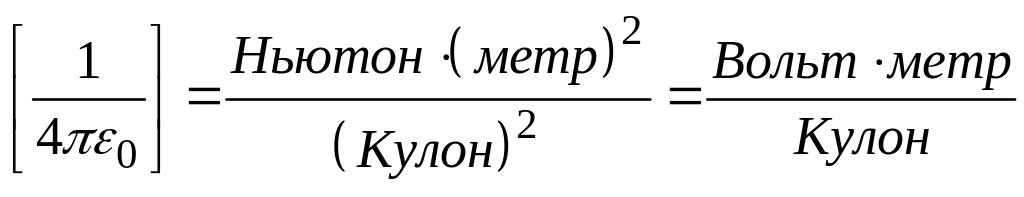где
м/сек
– скорость света в вакууме. Отсюда
ед. СИ.
Для количественной характеристики
электрического поля служит векторная
физическая величина – напряженность
электрического поля. Напряженность
электрического поля
- это сила, действующая со стороны прочих
зарядов на единицу заряда
.
Из закона Кулона (3.2), разделив обе части
равенства на
,
получаем напряженность электрического
поля заряда
.
(3.3)
Если зарядов много, то поле
в любой точке равно сумме вкладов всех
зарядов
,
где
-
заряд с номером
,
-
расстояние от пробного заряда
до заряда
.
Рассмотрим поток вектора электрического
поля точечного заряда
через замкнутую электрическую поверхность
,
окружающую заряд и имеющую центр в точке
нахождения заряда. За положительное
направление нормали к поверхности
выберем направление внешней нормали,
как показано на рисунке 4.
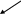
Заряд , окруженный сферой
Рис. 4
Из материала 3-го семестра курса высшей
математике известно (см.
,
гл. 15, §5, §8), что поток векторного поля
определяется как интеграл, взятый по
поверхности
(3.4)
Здесь
– поток поля
через поверхность S,
- единичная нормаль к поверхности. В
нашем случае векторное поле дается
выражением (3.3), S –
сфера, уравнение которой
,
,
R – зарядный радиус
сферы,
- внешняя единичная нормаль к сферической
поверхности.
Для электрического поля на поверхности сферы радиуса R имеем
.
Поэтому вынося за интеграл постоянную величину выражения для потока поля (3.4) примет вид
.
Интеграл в правой части последнего равенства представляет собой площадь поверхности сферы. Таким образом, получаем
. (3.5)
Полученный результат показывает, что поток вектора электрического поля через сферическую поверхность не зависит от радиуса сферы, окружающей заряд, т. е. один и тот же для любой другой концентрической с ней сферы.
В том случае, когда заряд находится вне сферы поток вектора через ее поверхность будет равен нулю – “втекающий” поток поля равен “вытекающему” потоку. Эти выводы можно записать так:
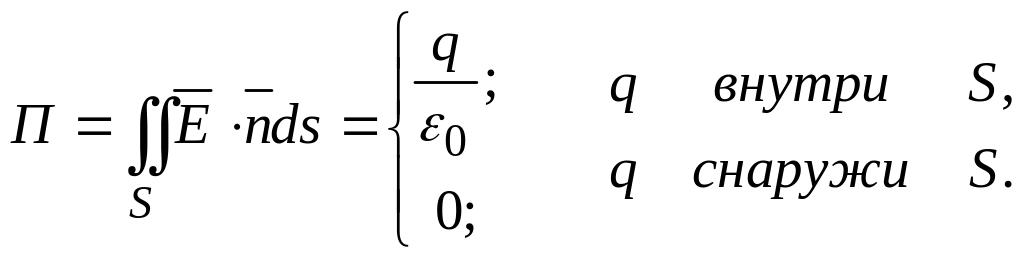(3.6)
Преобразуем теперь интеграл в (3.6), взятый по замкнутой поверхности, в интеграл по объему с помощью формулы Остроградского – Гаусса
,
(3.7)
где дивергенция вектор – функции
в декартовых координатах выражается
так
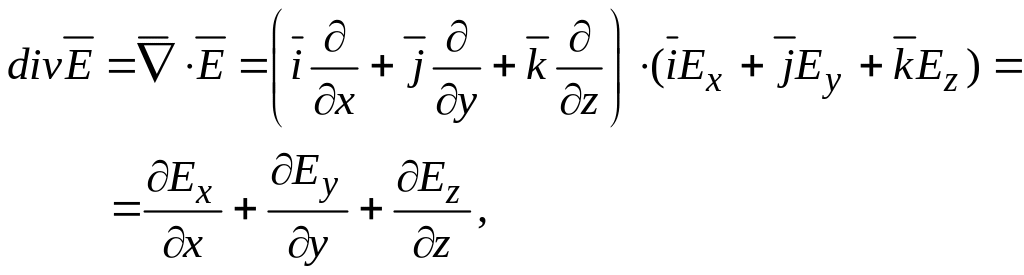(3.8)
-
оператор Гамильтона, V
– объем, ограниченный поверхностью S.
Правую часть формулы (3.6) также можно
представить как интеграл по объему
,
(3.9)
где
-
плотность заряда в объеме V.
Приравнивая правые части выражения (3.7) и (3.9), получим
.
Отсюда получаем, в виду произвольности объема V, одно из уравнений Максвелла
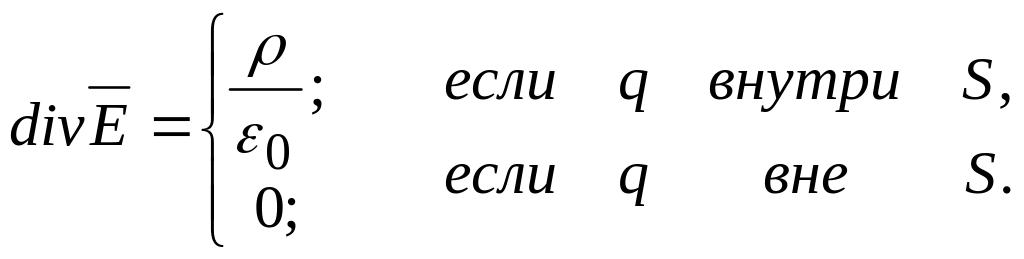(3.10)
Уравнение (3.10) остается справедливым и
в том случае когда заряд распределен в
объеме, т.е. когда плотность заряда
является функцией координат точки
.
Поскольку поле стационарного распределения
зарядов является потенциальным, то
введем скалярный потенциал
. (3.11)
Тогда левая часть (3.10) принимает вид
.
Представляя этот результат в уравнение
(3.10) в случае
получим дифференциальное уравнение
Пуассона
которое при отсутствии в рассматриваемой области зарядов, переходит в дифференциальное уравнение Лапласа
К уравнениям Пуассона и Лапласа приводит не только рассмотренная задача о потенциале электрического поля. К этим же уравнениям приводят многие другие задачи математической физики.