Задача №4

Задание. Вычислите приближенно интеграл

при по формулам: 1) трапеций; 2) Симпсона.

Вычислите точное значение интеграла и сравните его с полученными приближенными значениями.

Решение. Точное значение определенного интеграла вычисляется по формуле Ньютона-Лейбница через первообразную :

.

Если же первообразная неизвестна или функция задана таблицей или графиком, то применяются методы приближенного интегрирования. Формулы для приближенного интегрирования получаются при замене площади криволинейной трапеции на сумму площадей простых геометрических фигур, площадь которых легко вычисляется.

Разделим интервал на равных частей длиной . При этом . Обозначим через значение функции в точках .

Метод трапеций. Если площадь каждой полоски, на которые разбита криволинейная трапеция точками , считать приближенно равной площади соответствующей трапеции, то для вычисления интеграла получаем формулу трапеций (рис. 3)

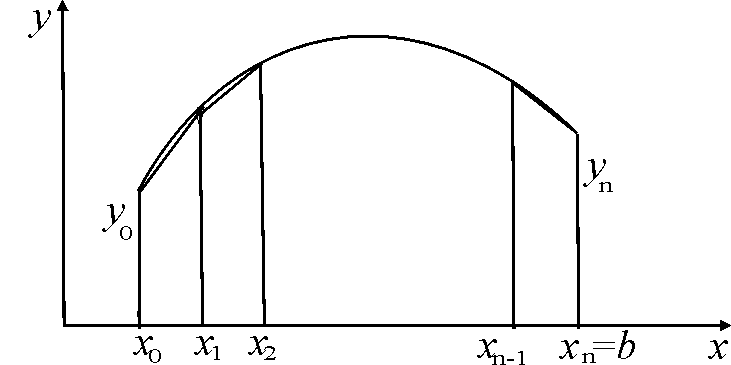
Рис. 3

Метод Симпсона. Метод Симпсона применим при разбиении интервала на четное число частей . Каждая пара полосок ограничивается сверху параболой, проходящей через три точки. Затем вычисляется площадь каждой пары полосок, ограниченной сверху параболой. Сумма площадей всех пар полосок является приближенным значением определенного интеграла (рис. 4).

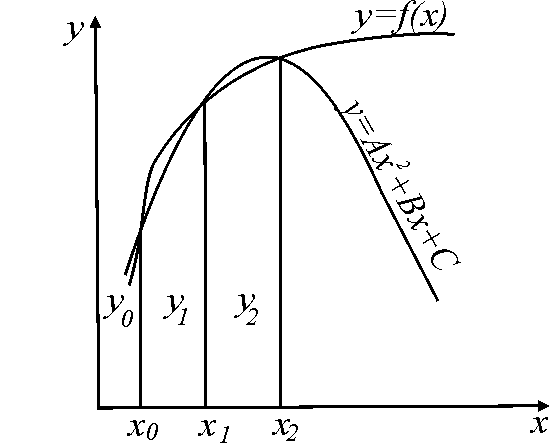
Рис. 4

1) Согласно условию , поэтому

Расчетная формула имеет вид

где , .

Все вычисления приведены в таблице 6:

Таблица 6

0 1 2 3 4 5	0.8 1.1 1.4 1.7 2.0 2.3	0.696 0.868 0.995 1.087 1.155 1.205
7 8	2.9 3.2	1.271 1.294

Таким образом,

.

2) Расчетная формула имеет вид

где , .

Следовательно,

.

3) Вычислим значение этого интеграла с помощью формулы Ньютона-Лейбница. Имеем

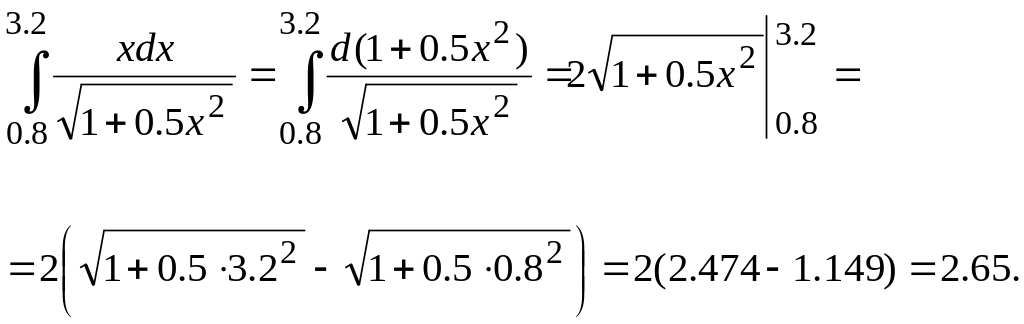
Вывод. Результаты, полученные в пунктах 1) и 2) , действительно приближают точное значение интеграла, полученное в пункте 3). Более точный результат получен с помощью формулы Симпсона.

Задача №6

Задание. С помощью метода Эйлера составьте таблицу приближенных значений решения дифференциального уравнения , удовлетворяющего начальному условию , на отрезке с шагом

, .

Решение. Задача Коши для обыкновенного дифференциального уравнения, разрешенного относительно производной

(1)

состоит в том, чтобы найти решение этого уравнения, удовлетворяющее начальному условию

. (2)

Простейшим численным методом решения задачи Коши является метод Эйлера, называемый иногда методом ломаных Эйлера.

Пользуясь тем, что в точке известно и значение решения и значение его производной , можно записать уравнение касательной к графику искомой функции в точке :

. (3)

При достаточно малом значении ордината

этой касательной, полученная подстановкой в правую часть (3) значения , по непрерывности должна мало отличаться от ординаты решения задачи (1)-(2). Следовательно, точка пересечения касательной с прямой может быть приближенно принята за новую начальную точку. Через эту точку снова проведем прямую

,

которая уже приближенно отражает поведение касательной к в точке . Подставляя сюда , получим приближение значения значением

и т.д. Продолжая вычисления в соответствии с намеченной схемой, получим формулу Эйлера для решения задачи Коши (1) - (2)

(4)

Геометрический смысл метода Эйлера заключается в том, что интегральная кривая на каждом отрезке , , …, заменяется отрезком касательной к интегральной кривой, проходящей через точки , а интегральная кривая заменяется ломаной, проходящей через точки , , …, . Эта ломаная называется ломаной Эйлера.

В нашем случае

Находим последовательные значения аргумента: , , , ,…, . Вычислим соответствующие значения искомой функции:

Результаты вычислений представим в таблице 7.

	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
	1	1.1	1.22	1.36	1.53	1.72	1.94	2.2	2.49	2.82	3.19

Таблица 7