Задача №2

Задание. Найдите приближенное решение системы методом простой итерации с точностью 0.01.

Решение. Пусть дана система линейных уравнений

(1)

Предполагая, что диагональные коэффициенты , разрешим первое уравнение системы (1) относительно , второе – относительно и т.д. Тогда получим эквивалентную систему

(2)

Где , при и при Введя матрицы

, , ,

систему (2) можем записать в матричной форме

. (3)

Для решения системы (3) применим метод последовательных приближений. За начальное приближение принимаем, например, столбец свободных членов .

Далее, последовательно строим матрицы-столбцы

, ,…. , , …

Если последовательность приближений имеет предел

,

то этот предел является решением системы (3) и, cледовательно, решением равносильной системы (1).

Для того чтобы процесс итераций сходился к единственному решению этой системы, независимо от выбора начального приближения, необходимо выполнение для приведенной системы (2) условия (достаточное условие сходимости метода итераций)

.

Приведем заданную систему уравнений к виду (2)

Отметим, что

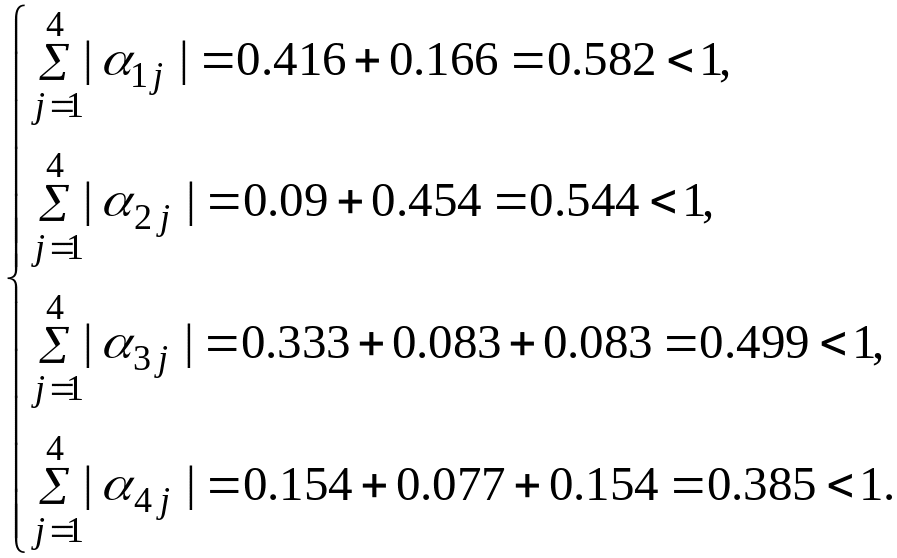
Таким образом, достаточное условие сходимости выполнено, поэтому итерационная последовательность приближенных решений будет сходиться к решению системы.

В качестве начального приближения возьмем систему чисел ; ; ; .

После первого шага получим:

После второго:

Результаты вычислений заносим в таблицу 2:

Таблица 2

0 1 2 3 4	0.166 0.033 0.0268 0.0351 0.0367	0.545 0.3553 0.3979 0.3825 0.3828	0.166 0.208 0.1739 0.1712 0.175	0.385 0.3175 0.3526 0.3502 0.3501

Поскольку при 4-ой итерации получившиеся значения отличаются от предыдущих не более, чем на 0.01, то решение с требуемой точностью достигается на 4-ой итерации и его можно взять в качестве ответа.

Задача №3

Задание. Отделите корни и найдите приближенное решение заданного уравнения с точностью 0.01 методом Ньютона и методом итераций .

Решение. Пусть дано уравнение с одним неизвестным вида

= 0,

где - непрерывная функция переменной . Требуется найти корень этого уравнения. Представить решение этого уравнения в виде конечной формулы оказывается невозможным, поэтому мы откажемся от поиска точного значения корней и займемся их приближенным вычислением с заданной точностью.

Решение задачи отыскания корней осуществляется в два этапа. Первый этап называется этапом отделения (локализации) корней, второй – этап итерационного уточнения корней.

Известно, что если функция непрерывна и принимает на концах отрезка значения разных знаков, т.е. , то внутри этого промежутка имеется хотя бы один корень уравнения.

Геометрически это означает, что график непрерывной функции, расположенной по разные стороны оси , пересекает эту ось, по меньшей мере в одной точке.

Отрезок , содержащий только один корень уравнения , называется отрезком локализации корня. Цель этапа локализации считается достигнутой, если для каждых подлежащих определению корней удалось указать отрезок локализации.

К сожалению, создать универсальный метод локализации корня не представляется возможным. В простых ситуациях хороший результат может давать графический метод. Часто применяется построение таблиц значений функции вида и, при этом о наличии корня на отрезке , судят по перемене знака функции на концах отрезка. Рассмотрим отделение корней на конкретном примере.

Пример. Локализуем корни уравнения

.

Для этого преобразуем уравнение к виду и построим графики функций и . Абсциссы точек пересечения этих графиков являются корнями данного уравнения.

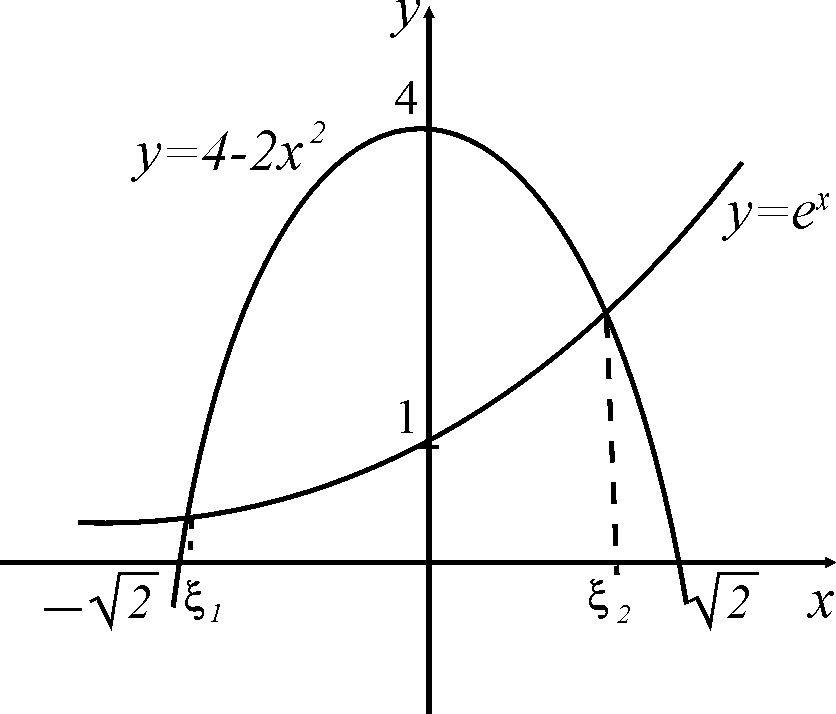
Рис. 1

Из рис.1 видно, что уравнение имеет два корня, расположенные на отрезках и .

Отделим корни уравнения табличным способом. Для этого составим таблицу значений функции (таблица 3).

Таблица 3

-3 -2 -1 0 1	-14.05 -4.14 1.63 3.00 -0.72

Из таблицы значений функции на промежутке с шагом изменения , равным 1, видно, что существуют корни на отрезках и , так как значения функции на концах отрезка имеют разные знаки.

После локализации корней производится итерационное уточнение каждого корня одним из существующих методов. Мы рассмотрим метод касательных и метод итераций.

1) Метод касательных. Если известно хорошее начальное приближение решения уравнения , то эффективным методом повышения точности является метод Ньютона (метод касательных). Метод состоит в построении итерационной последовательности .

Достаточные условия сходимости этого метода содержатся в следующей теореме.

Теорема. Пусть функция определена и дважды дифференцируема на отрезке , причем , а производные сохраняют знак на отрезке . Тогда, исходя из начального приближения , удовлетворяющего неравенству , можно построить последовательность сходящуюся к единственному на решению уравнения .

Геометрически метод Ньютона эквивалентен замене небольшой дуги кривой касательной, проведенной в некоторой точке кривой (рис. 2).

Выберем, например, , для которого . Проведем касательную к кривой в точке . В качестве первого приближения корня возьмем абсциссу точки пересечения этой касательной с осью . Через точку снова проведем касательную, абсцисса точки пересечения которой даст второе приближение корня и т. д. (рис. 2).

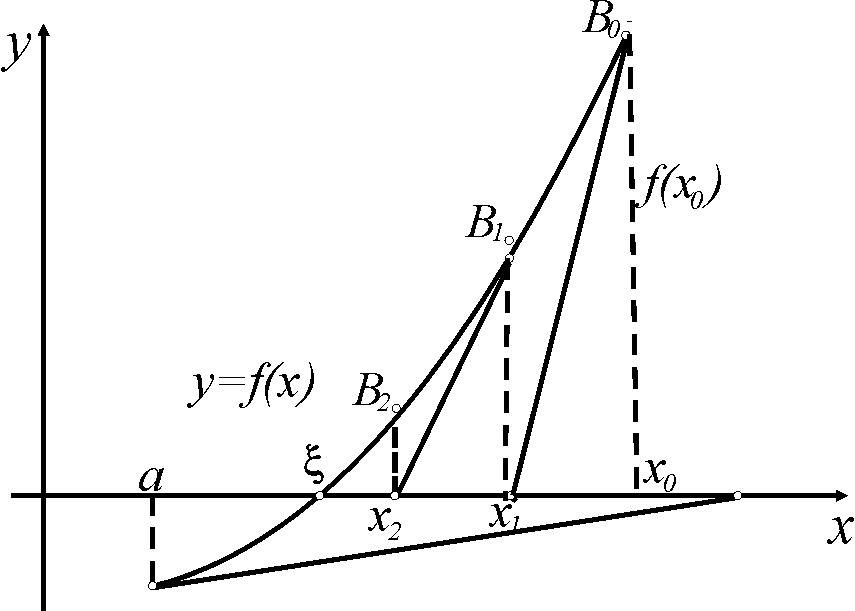
Рис. 2

Вернемся к исходной задаче. Обозначим . Найдем производную данной функции .

Составим таблицу знаков функции:

	-	-3	-2	-1	0	1	2	3
	+	+	-	-	-	-	-	+	+

Уравнение имеет два действительных корня, лежащих в промежутках , . Уточним один из этих корней, например, принадлежащий отрезку , методом касательных. Для выбора начального приближения найдем , . Так как и , то за начальное приближение принимаем .

Для вычислений применяем формулу Ньютона

Результаты занесем в таблицу 4:

Таблица 4

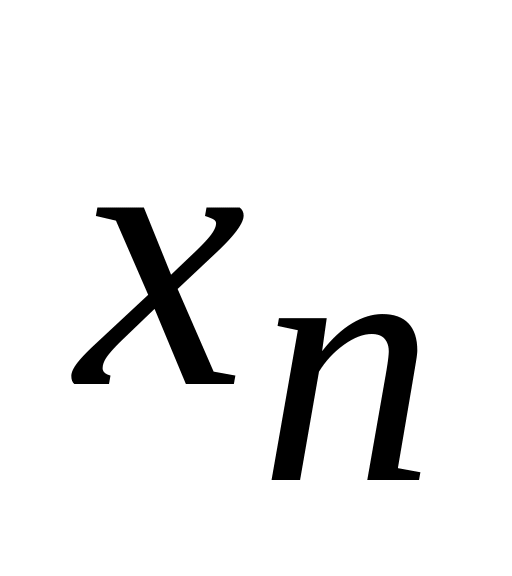
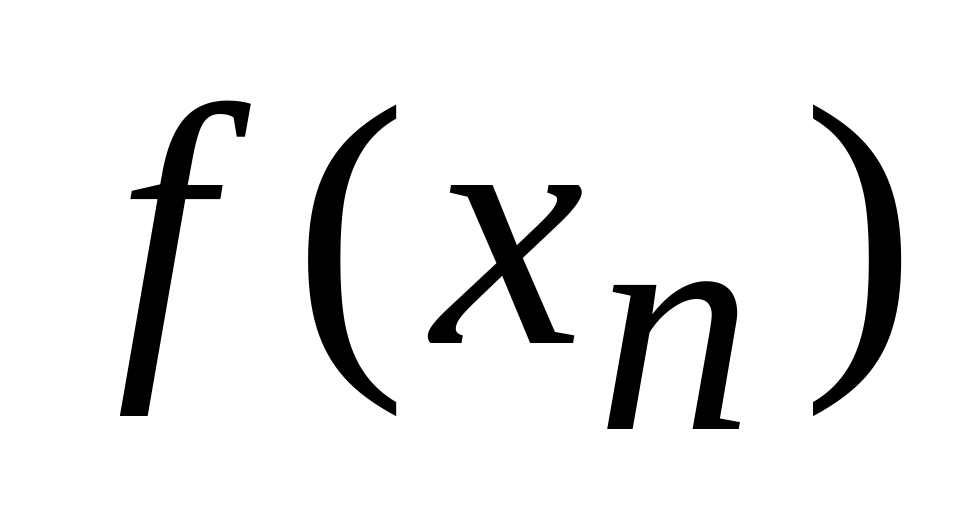
0 1 2 3 4	3 2.438 2.138 2.048 2.04	54 14.418 2.76 0.201 0.0014

Поскольку , то решение с точностью 0.01.

2) Метод итераций. В основе методы итераций лежит принцип сжимающих отображений.

Теореме (принцип сжимающих отображений). Если функция - непрерывна и дифференцируема и , то у функции есть неподвижная точка, т.е. на [a,b] существует решение уравнения . Причем если , то последовательность сходится к этому решению и .

Для уточнения корня методом итераций приведем уравнение к виду . При этом должно выполняться условие для . Функцию будем искать из соотношения , считая, что , где число имеет тот же знак, что и в промежутке . Известно, что .

Так как , то можно взять . Тогда

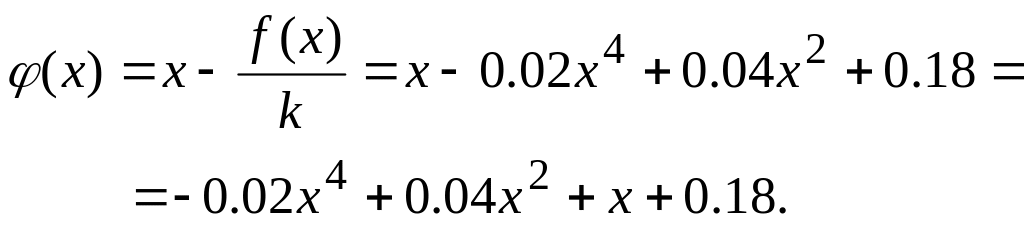
Пусть , тогда . Вычисления располагаем в таблице 5.

Таблица 5

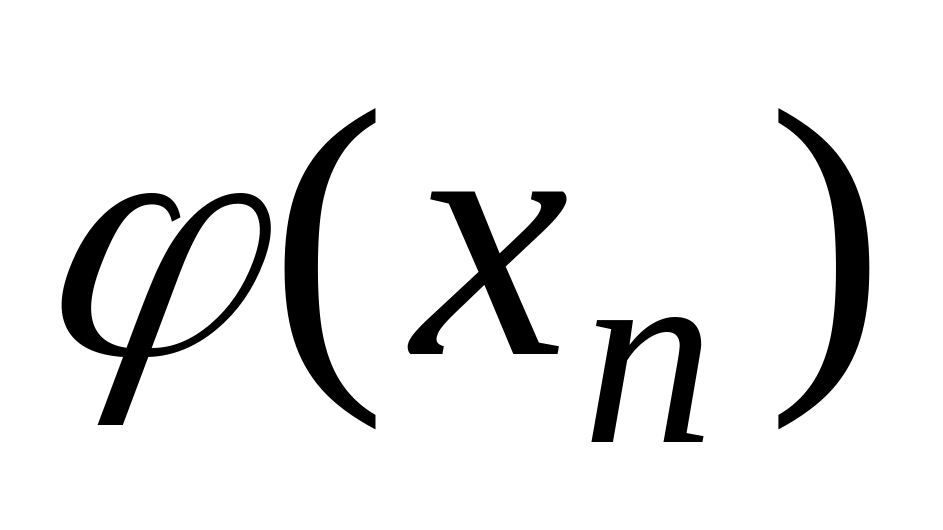
0 1 2 3 4	2 2.02 2.0302 2.0353 2.0378	0.2 0.1902 0.1887 0.1879 0.1876

Требуемая точность достигается на 3-ем шаге, поэтому .