ФГБОУ ВО «Воронежский государственный

технический университет»

Кафедра физики твердого тела

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

для практических и семинарских занятий по дисциплине

«Практикум по физике твердого тела» для студентов

направления 16.03.01 «Техническая физика» (профиль «Физическая электроника») очной формы обучения

Воронеж 2016

Составитель канд. физ.-мат. наук Л.И. Янченко

УДК 538.9

Методические указания для практических и семинарских занятий по дисциплине «Практикум по физике твердого тела» для студентов направления 16.03.01 «Техническая физика» (профиль «Физическая электроника») очной формы обучения / ФГБОУ ВО «Воронежский государственный технический университет»; сост. Л.И. Янченко. Воронеж, 2016. 28 с.

Методические указания содержат краткие теоретиче-ские и практические сведения в области физики твердого тела в соответствии с рабочей программой лекционного курса по теме кинетические явления в полупроводниках.

Методические указания подготовлены в электронном виде в текстовом редакторе MS Word 2007 и содержатся в файле Мет. практикум по ФТТ.doc.

Табл. 1. Ил. 8. Библиогр.: 6 назв.

Рецензент канд. физ.-мат. наук, доц. В.В. Ожерельев

Ответственный за выпуск зав. кафедрой

д-р физ.-мат. наук, проф. Ю.Е. Калинин

Издается по решению редакционно-издательского совета Воронежского государственного технического университета

Ó ФГБОУ ВО «Воронежский государственный технический университет», 2016

1. КИНЕТИЧЕСКИЕ ЯВЛЕНИЯ В ПОЛУПРОВОДНИКАХ

1.1. Неравновесная функция распределения

При описании явлений переноса с помощью кинетического уравнения Больцмана необходимо знание неравновесной функции распределения для электронов и дырок. Ее определение проведем для невырожденного полупроводника, находящегося в электрическом и магнитном полях и имеющего градиент температуры. Для полупроводника со сферическими изоэнергетическими поверхностями энергия электронов

(1.1)

а их скорость

(1.2)

При наличии внешних полей – электрического напряженностью ε и магнитного с индукцией В – на электрон действует сила

(1.3)

1.2. Удельная электрическая проводимость полупроводников

Рассчитаем удельную электрическую проводимость однородного невырожденного полупроводника при отсутствии градиента температуры (∇T = 0) и магнитного поля (В = 0), изоэнергетические поверхности которого представляют собой сферы. Пусть проводник находится в постоянном однородном электрическом поле напряженностью ε.

В элементе объема dτ_k кристалла единичного объема количество электронов

(1.4)

Эти электроны, движущиеся под действием внешнего электрического поля со скоростью v, создают элементарную плотность тока

(1.5)

Если в полупроводнике имеется два сорта носителей заряда, то полная плотность тока

(1.6)

где v_n, f_n(k) и v_p, f_p(k') – скорость и неравновесная функция распределения электронов и дырок соответственно. Интегрирование нужно проводить по всей зоне Бриллюэна.

Если в (1.6) поставить равновесную функцию распределения f₀, то

(1.7)

где f₀(k) – четная функция, a vf₀(k) = kf₀(k) – нечетная функция и дает нуль при интегрировании в симметричных пределах.

Выражение (1.7) означает, что при термодинамическом равновесии в веществе нет тока.

Если, например, неравновесная функция

(1.8)

то с учетом (1.7) вместо выражения (1.6) будем иметь:

(1.9)

Поскольку полупроводник однородный, то ∇_rf = 0 и при отсутствии градиента температуры (∇T = 0)

∇F = 0. (1.10)

При наличии электрического поля ε = - ∇φ и отсутствии магнитного поля (В = 0), учитывая (1.10), получаем:

(1.11)

(1.12)

Используя (1.11), плотность электронного тока запишем в виде

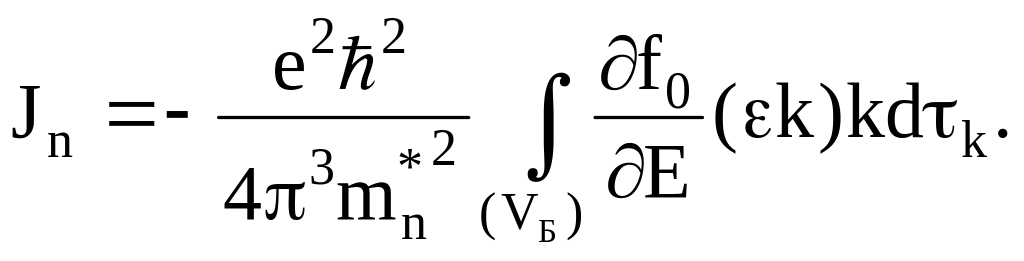(1.13)

Для невырожденного полупроводника при отсчете энергии от дна зоны проводимости количество электронов в зоне проводимости определяется соотношением

(1.14)

Поскольку для невырожденного состояния f₀ = e ^{– (E – F)/kT}, то

(1.15)

Подставляя (1.15) в (1.13), получаем

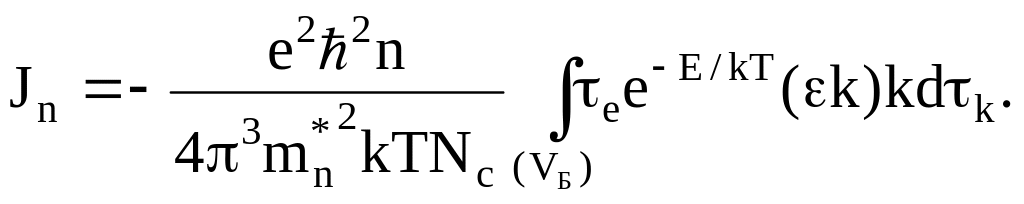(1.16)

Если воспользоваться соотношением

(1.17)

то (1.16) запишем в виде

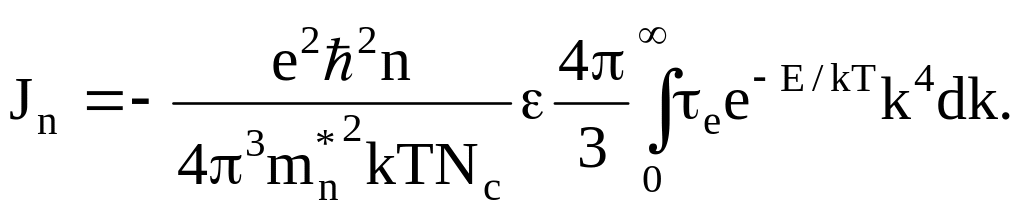(1.18)

Полагая α = E/kT, будем иметь:

(1.19)

а подставляя (1.19) в (1.18) и учитывая, что , получаем:

(1.20)

Введем обозначение

(1.21)

Тогда

(1.22)

где

(1.23)

– дрейфовая подвижность, а

(1.24)

– удельная проводимость, обусловленная электронами.

Соответственно дырочная составляющая тока

(1.25)

Здесь среднее время релаксации дырок

(1.26)

дрейфовая подвижность дырок

(1.27)

и удельная проводимость, обусловленная дырками

(1.28)

Следовательно, полная плотность тока в полупроводнике, имеющем два типа носителей заряда, равна:

(1.29)

где – удельная проводимость полупроводника.