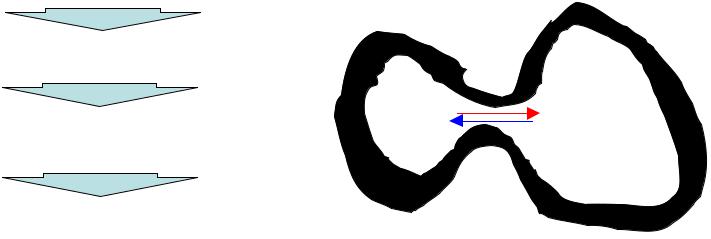
Равновесная плотность энергии излучения
Полости со стенками из различных материалов.
Т1 > Т2
u1(T) > u2(T) -отсутствие |
T1 |
T2 |
равновесия |
||
Φ1 2 > Φ2 1 |
1 |
2 |
|
||
|
|
|
1: излучает больше, чем поглощает. |
u |
u2 |
1 |
|
|
2: поглощает больше, чем излучает, |
|
|
T1 T2
Два тела приобретают одинаковую температуру в результате обмена между собой только тепловой энергией.
21
Равновесная плотность энергии излучения
Необратимость процесса, при котором не происходит других изменений, кроме передачи теплоты от горячего тела к холодному.
Невозможность передачи теплоты от холодного тела к горячему без каких-либо других изменений в системе.
22
Равновесная плотность энергии излучения
Независимость равновесного излучения от природы стенок полости.
Стенки абсолютно черного тела: поглощение всего потока энергии Φ, падающего на них и
излучение такого же потока энергии Φ.
Стенки серого тела:
поглощение части aΦ потока энергии Φ, падающего на них, отражение части (1-a)Φ и излучение части aΦ.
23
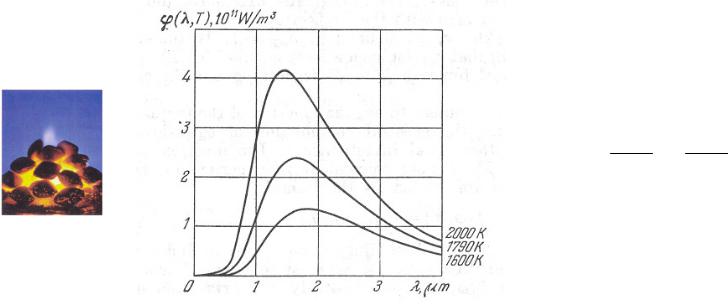
Закон Стефан-Больцмана |
r T |
f ( ,T ) |
|
a T |
|||
|
Экспериментально наблюдаемое спектральное распределение излучения абсолютно черного тела при различных T.
( ,T ) 2 c f ( 2 c ,T )
2
Соответствие между площадями под кривыми и радиационной способностью RT
абсолютно черного тела при соответствующих T.
T RT
Смещение максимума ( ,T)
к более коротким λ при росте T.
24
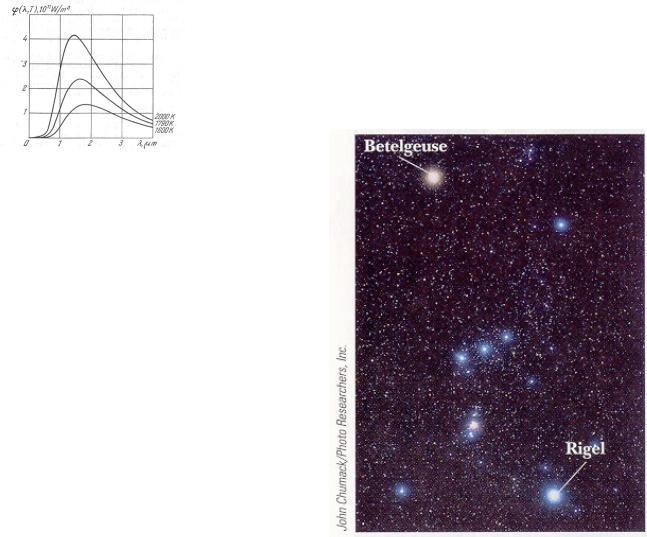
Закон Стефан-Больцмана
Какая из двух звезд горячее?
25
26
Закон Стефан-Больцмана
1879: австрийский физик Джозеф Стефан (1835-1893): энергетическая светимость R любого тела пропорциональна неверно
4-й степени абсолютной температуры. |
|
|
1884: австрийский физик Людвиг Больцман (1844-1906): |
верно |
|
энергетическая светимость R* абсолютно черного тела |
||
|
||
|
|
R* f ( ,T )d T 4 .
0 |
лучеиспускательная |
|
|
|
способность |
Постоянная Стефан-Больцмана |
абсолютно черного тела |
5,7 10 8 Вт/(м2 K4 )
27
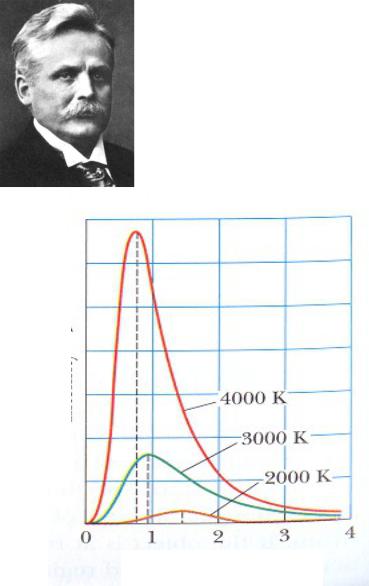
Закон смещения Вина
1893: немецкий физик Вильгельм Вин (1864-1928):
Интенсивность →
Длина волны, мкм
Закон смещения Вина mT b
o
b 2,90 10 3 м K 2,90 107 A K
28
Формула Рэлея-Джинса
Английские физики лорд Рэлей (Джон Уильям Стретт) (1842-1919)
и Джеймс Джинс (1877-1946).
Равновесное излучение в полости – система стоячих э-м волн.
Плотность равновесного излучения u ,T 2 2 3 kT
c
Лучеиспускательная способность абсолютно черного тела
f ,T 4c u ,T
Формула Рэлея-Джинса f ,T 22 2 kT
4 c
29
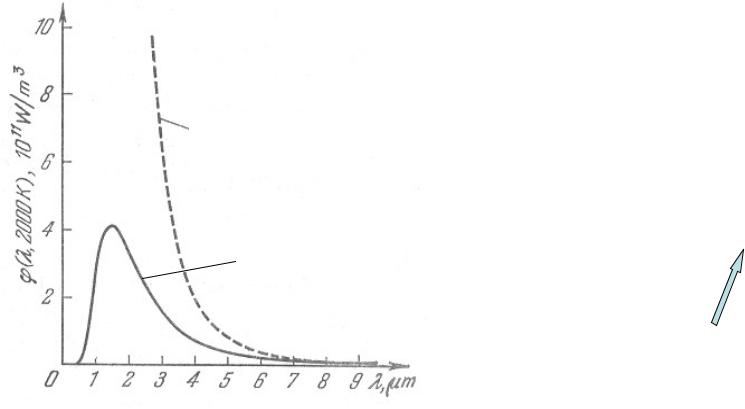
Экспериментальное распределение энергии
u ,T |
2 |
kT |
|
2c3 |
|||
Формула Рэлея-Джинса |
|
||
|
|
формула Рэлея-Джинса
Эксперимент
Результат расчета энергия равновесного излучения по формуле Рэлея-Джинса
u(T ) u( ,T )d
0
Ультрафиолетовая
катастрофа:
Короткие волны: |
Длинные волны: |
противоречие |
|
с экспериментальными |
|||
неудовлетворительное |
удовлетворительное |
||
данными - |
|||
согласие |
согласие |
||
- |
+ |
30 |
|
|
|
u(T) конечна. |