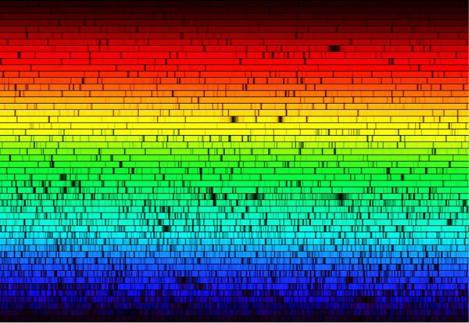
Дискретный линейный спектр поглощения
Обнаружение химического элемента He (гелия) -
результат анализа спектра поглощения газов в атмосферах Солнца и Земли.
Спектр звезды Арктур в высоком разрешении (Национальная обсерватория Китт-Пик, США).
Дискретный спектр поглощения – информация («паспорт») о химическом составе атмосферы звезды.
11
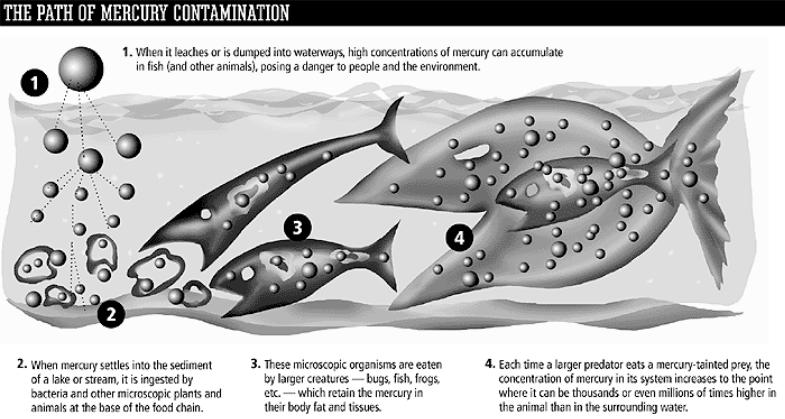
Дискретный линейный спектр поглощения
Метод атомно-абсорбционной спектроскопии – первые свидетельства высокого содержания ртути в мясе тунца.
12
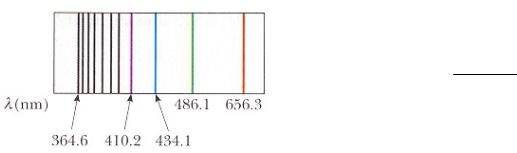
Закономерности в спектре атома водорода
1860-1885: аккумулирование учеными большого количества полученных спектроскопическими методами данных об эмиссии света атомами.
1885: получение швейцарским учителем Якобом Бальмером (1825-1898) эмпирического уравнения, корректно предсказывающего длины волн четырех видимых линий в спектре поглощения водорода:
H (красная), H (зеленая), H (синяя), H (фиолетовая).
n2
0 n2 4 , где 0 = const
Полный набор этих и других линий в УФ диапазоне эмиссионного спектра водорода - серия Бальмера.
Граница H серии Бальмера - линия с меткой 364,6
(линия с самой короткой длиной волны в УФ диапазоне э-м спектра).
13
Закономерности в спектре атома водорода
Модификация исходного уравнения Бальмера шведским спектроскопистом Йоханессом Ридбергом (1854-1919):
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
n 3, |
4, |
5, |
. . . |
серия Бальмера |
|||||
|
|
|
|
RH |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
22 |
|
|
n2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
R – постоянная Ридберга |
|
R |
H |
= 109737.309 0.012 cм-1 |
||||||||||||||||
|
|
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
n 2, |
3, |
4, |
. . . |
серия Лаймана |
||||||||
|
|
|
|
RH |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
12 |
|
n2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
n 4, |
5, |
6, |
|
. . . |
серия Пашена |
||||
|
|
|
|
RH |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
32 |
|
|
|
n2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
n 5, |
6, |
7, |
|
. . . |
серия Брэккета |
||||
|
|
|
|
RH |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
42 |
|
|
|
|
n2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
n 6, |
7, |
8, |
|
. . . |
серия Пфунда |
||||
|
|
|
|
RH |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
52 |
|
|
|
|
n2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Закономерности в спектре атома водорода
|
|
1 |
|
|
1 |
|
1 |
|
|
Обобщенное уравнение |
|
RH |
|
|
|
|
|
|
|
m2 |
n2 |
|||||
|
|
|
|
|
|
|||
n |
= 2 = 2 с/ 2 сR /m2 |
= R/m2 – предел серии. |
||||||
|
|
H |
|
|
|
|
|
|
Возможность расчета частоты, соответствующей произвольной линии в спектре атома водорода, как разницы между двумя числами вида T(n) = R/n2
= T1 (m) – T2 (n).
T(n) = R/n2 – спектральный терм или просто терм.
15
Содержание сегодняшней лекции
Aтомная физика
Ранние модели атома
Модель Томсона. Модель Резерфорда.
Эксперимент Франка-Герца. Боровская модель атома водорода. Боровский принцип соответствия.
16
Ранние модели атома
17
Ранние модели атома
Демокрит (460-371 гг. до н.э.) - времена Ньютона (1642-1727):
Материя – бесконечное число мельчайших неделимых частиц - атомов.
Бесчисленное множество разнообразных вещей и свойств – результат различного сочетания атомов.
Движение атомов – результат влияния господства необходимости.
18
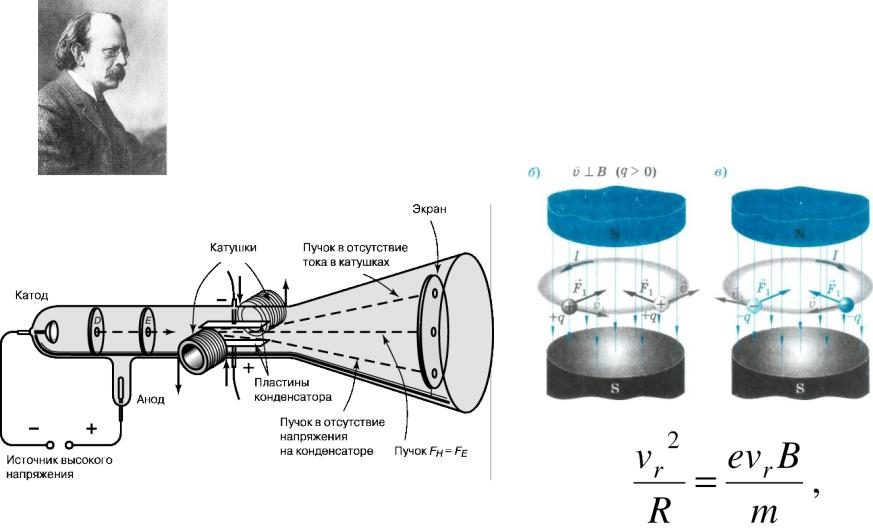
Ранние модели атома
1897: открытие электрона и определение его удельного заряда английским физиком Джозефом Джоном Томсоном (1856-1940).
19
Модель Томсона
Дж.Дж. Томсон (1898 г. ): модель атома «сливовый пудинг» - атом как область, в которой электроны распределены внутри положительного заряда ядра (изюминки в высоком пудинге).
20