Прохождение частицы через потенциальный барьер
Экспериментальные результаты
-распад:
эмиссия -частиц (ядер атомов гелия) из нестабильных, тяжелых ядер –
одна из форм радиоактивного распада.
Квантовая механика:
возможность проникновения -частицы сквозь барьер,
высота которого в несколько раз больше, чем энергия системы, состоящей из ядра и -частицы.
21
Прохождение частицы через потенциальный барьер
Экспериментальные результаты
Ядерный синтез:
сближение протонов на такое маленькое расстояние, что происходит их синтез и формирование ядра дейтерия во время реакции,
разогревающей Солнце и косвенно почти все вещество в Солнечной системе.
Классическая физика:
отсутствие возможности для протонов преодолеть барьер, существование которого вызвано
их взаимным электростатическим отталкиванием.
22
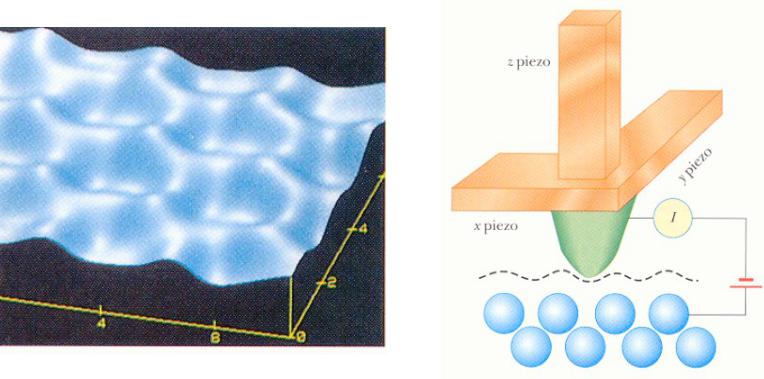
Прохождение частицы через потенциальный барьер
Экспериментальные результаты
Сканирующий электронный микроскоп – устройство для наблюдения изображения с горизонтальным разрешением до 0,2 нм и вертикальным разрешением до 0,001 нм.
23
Простой гармонический осциллятор
24
Простой гармонический осциллятор
Излучение абсолютно черного тела
Классический подход
Излучение в полости - установление стоячих э-м волн в результате излучения, вызванного колеблющимися в ее стенках заряженными частицами.
Потенциальная энергия системы U 12 kx2 12 m 2 x2, где 
k/m.
Колебания заряженной частицы в стенках полости между положениями x = - A и x = A, где A – амплитуда колебаний.
Общая энергия колеблющейся частицы E K U 12 kA2 12 m 2 A2 .
Возможность колебаний с любым значением энергии E.
Возможность реализации состояния с E = 0, соответствующей общей энергии частицы в покое при x = 0.
25
Простой гармонический осциллятор
Излучение абсолютно черного тела
Квантово-механический подход |
|
|
|
|
|
|
||||||||||||
Уравнение Шредингера |
|
2 |
d 2 |
U E . |
|
|
|
|||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
2m dx2 |
|
|
|
|
|
|
|
|||
1 |
2 |
|
2 |
|
2 |
|
d 2 1 |
2 |
|
2 |
|
|
|
|
||||
U 2 m |
|
x |
|
|
|
dx2 2 m |
x E |
|
|
|
||||||||
|
|
2m |
|
1 |
|
|||||||||||||
Решение для основного состояния: Be |
Cx2 |
. |
C |
m |
и E |
|
. |
|||||||||||
|
|
2 |
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решения для возбужденных состояний – 2 более сложны, но также с экспоненциальным множителем e Cx .
Квантованные значения энергии гармонического осциллятора
|
1 |
|
n 0, 1, 2, ... |
En n |
2 |
|
|
|
|
|
Сравнение с уравнением Планка: в последнем уравнении к n добавлена ½.
26
|
1 |
|
|
n 0, 1, 2, ... |
En n |
2 |
|
||
|
|
|
|
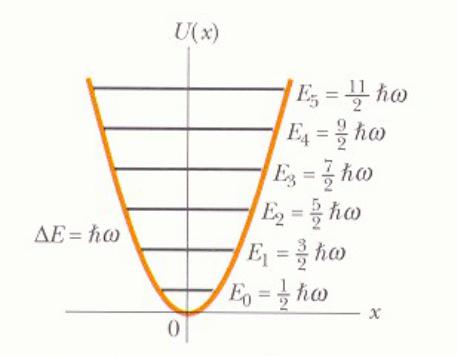
Простой гармонический осциллятор
n 0 E0 12
n 1 E1 32
…………………
E
Одинаковое расстояние между уровнями энергии.
27
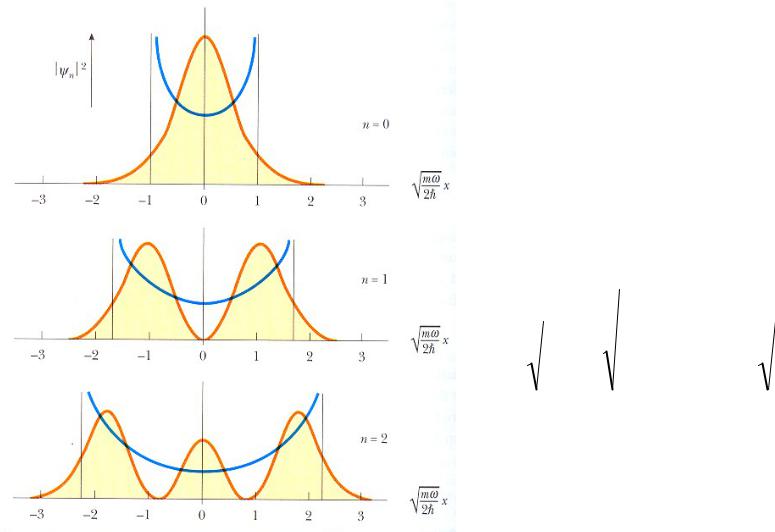
Простой гармонический осциллятор
Плотности вероятностей для трех первых состояний гармонического осциллятора.
классический подход
квантово-механический подход
Е U 12 m 2 x2
|
|
|
1 |
2 |
|
2 |
|
|
|
|
U |
|
2 m |
x |
|
|
|
m |
x |
||
E |
|
|
|
|||||||
|
|
|
|
|
|
|
|
2 |
||
Увеличение n – улучшение
соответствия между классическим и квантово-механическим подходами.
28
АТОМНАЯ ФИЗИКА
29
Контрольный вопрос
Частица совершает простые гармонические колебания в состоянии n = 0.
Наиболее вероятные значения координаты x
положения частицы согласно квантовой механике:
(a) x = 0 (б) x = A (в) все значения x равновероятны.
30