Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

«ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ» (ТУСУР)

Кафедра телекоммуникаций и основ радиотехники (ТОР)

Исследование разветвленной линейной цепи при гармоническом воздействии

Лабораторная работа по дисциплине «Теория электрических цепей»

Студенты гр. 120-1

___________Е.Д. Бормотов

«__» ______ 20__ г.

Дата

Руководитель

преподаватель каф. РТС

___________А.И. Попова

«__» ______ 20__ г.

Дата

Томск 2021

Оглавление

Оглавление 2

1 Краткие теоретические сведения 4

2 Домашнее задание 9

3 Описание экспериментальной установки и методики измерений 12

4 Экспериментальные результаты и их анализ 14

4.1 Определение токов ветвей и проверка выполнения первого закона Кирхгофа 14

4.2 Определение комплексных значений напряжений на элементах схемы и проверка выполнения второго закона Кирхгофа 14

4.3 Определение комплексных мощностей для элементов схемы и проверка баланса мощностей 14

5 Заключение 16

Цель работы:

1. Закрепление навыков расчета и измерения комплексных значений напряжений и токов электрических цепей.

2. Экспериментальная проверка выполнения законов Кирхгофа в комплексной (векторной) форме.

1. Краткие теоретические сведения

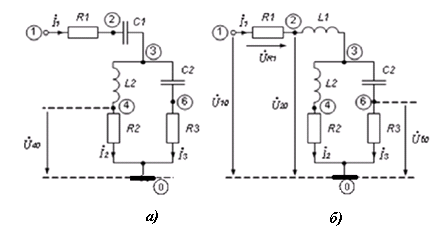
Рисунок 2.1 Исследуемые схемы

Схемы рис. 2.1 с помощью эквивалентных преобразований можно привести к схемам, представленным на рис.2.2. На рис. 2.2а сопротивления Z₁, Z₂, Z₃ определяются как последовательное соединение двух элементов, а Z₂₃ на рис. 2.2б как параллельное соединение Z₂ и Z₃.

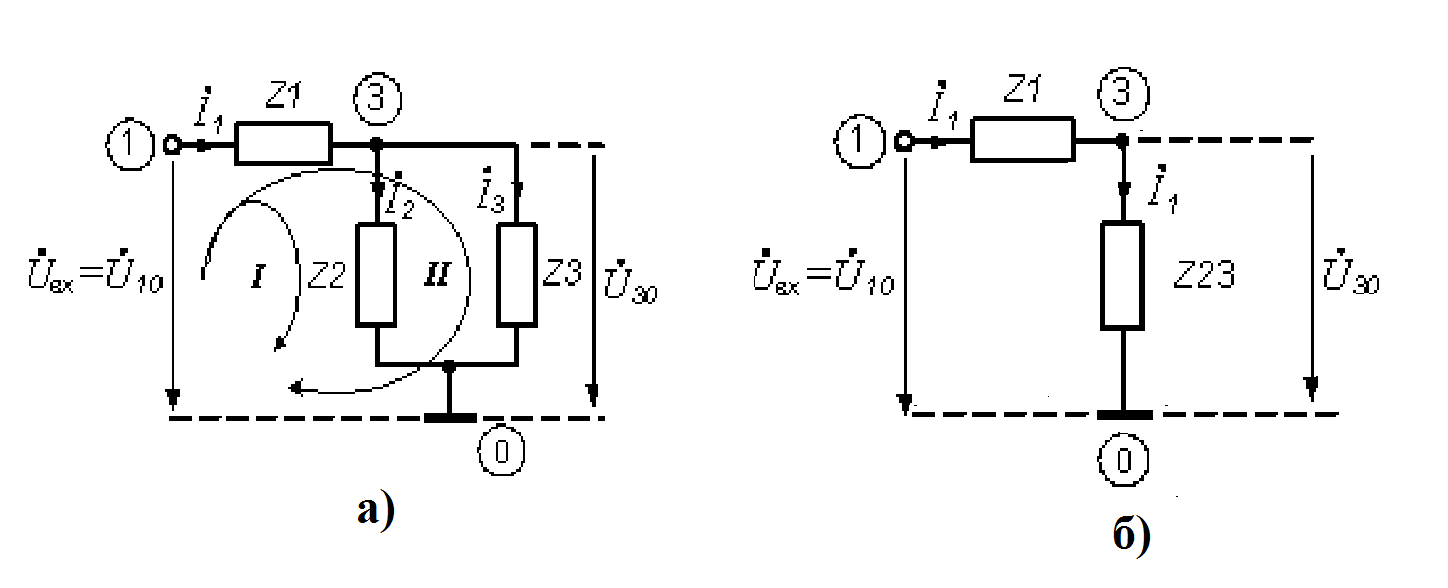
Рисунок 2.2 Эквивалентные преобразования схемы

Для расчета токов и напряжений на элементах используются закон Ома и два закона Кирхгофа в комплексной форме. Основные расчетные соотношения приведены ниже.

Сопротивление индуктивности определяется выражением 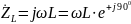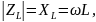(2.1):

, (2.1)

емкостное сопротивление определяется выражением, представленным ниже:

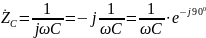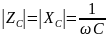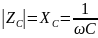, , (2.2)

где L и C  ‑ значение индуктивности или емкости;

ω=2πf – угловая частота входного сигнала.

Элементы соединены последовательно, если через них протекает один и тот же ток. Входное сопротивление участка цепи с последовательным соединением двух сопротивлений Z1 и Z2 имеет вид:

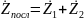. (2.3)

Элементы соединены параллельно, если на них действует одно и то же напряжение, т.е. они подключены к одной и той же паре узлов. Входное сопротивление участка цепи с параллельным соединением двух сопротивлений Z₁ и Z₂ имеет вид:

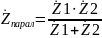. (2.4)

Закон Ома для участка линейной цепи в комплексной форме определяется выражением (2.5):

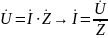, (2.5)

где 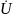 – напряжение, приложенное к зажимам участка электрической цепи,

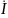 – ток через участок цепи,

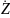 – комплексное сопротивление участка цепи.

I-ый закон Кирхгофа ‑ алгебраическая сумма комплексных токов в любом узле равна нулю. Знак тока определяется направлением тока относительно узла; условимся: входящие в узел токи брать со знаком «+», а выходящие со знаком «-».

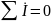, (2.6)

Пример для узла 3 электрической цепи рис.2.1 и рис. 2.2а:

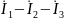=0. (2.6а)

II-ой закон Кирхгофа ‑  алгебраическая сумма комплексных значений напряжений в любом замкнутом контуре равна нулю (знак напряжения определяется его направлением относительно обхода контура):

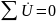, (2.7)

Тогда для электрической цепи рис.2.2а II-ый закон Кирхгофа для первого контура будет выглядеть следующим образом:

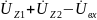=0, (2.7а)

для второго контура соответственно:

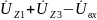=0. (2.7б)

Узловое напряжение 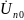– напряжение между узлом n и опорным узлом 0, заземленным на схемах рис. 2.1 и 2.2:

.

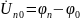Т.к. потенциал 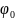опорного узла принят за нуль, то узловое напряжение численно совпадает с потенциалом узла n. Узловое напряжение всегда направленно к опорному узлу (рис.2.3).

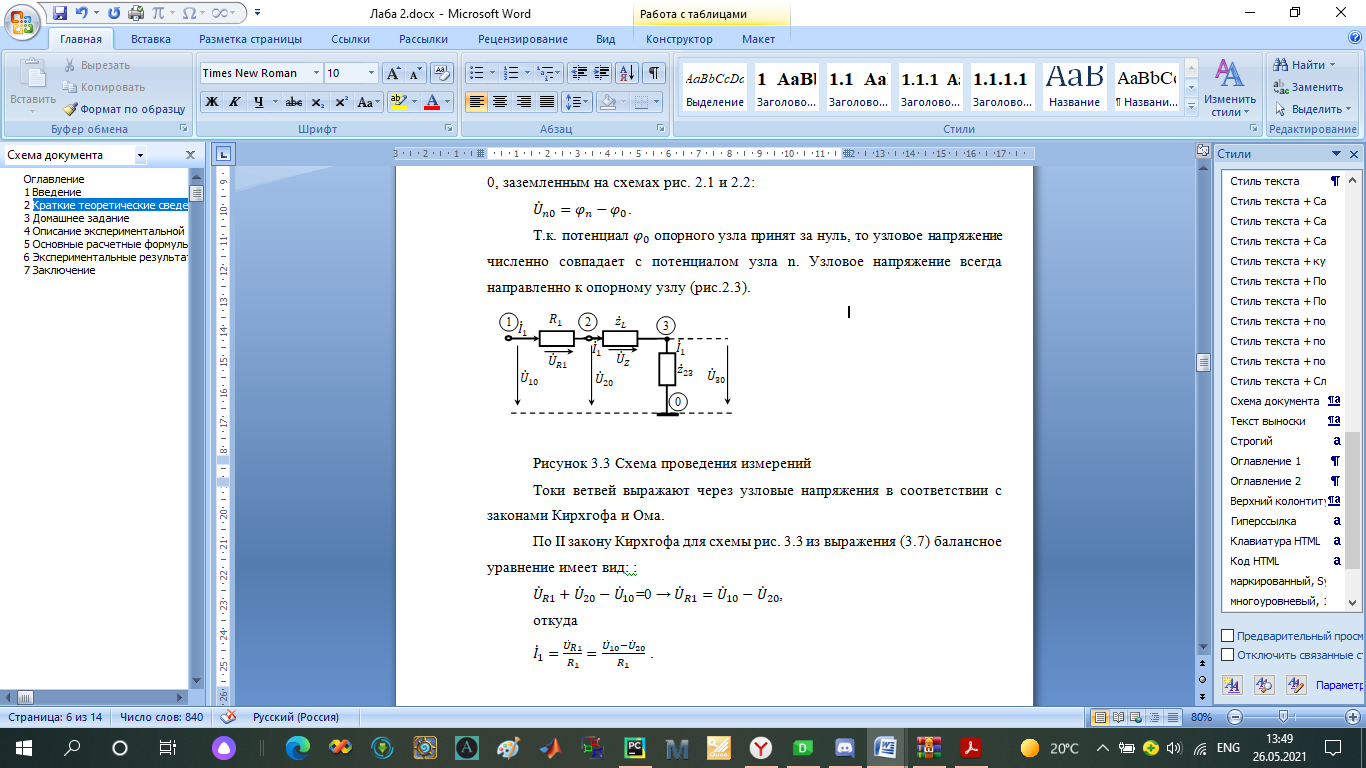
Рисунок 2.3 – Схема проведения измерений

Токи ветвей выражают через узловые напряжения в соответствии с законами Кирхгофа и Ома.

По II закону Кирхгофа для схемы рис. 2.3 из выражения (2.7) балансное уравнение имеет вид: :

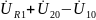=0 → ,

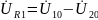откуда

.

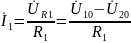Согласно закону Ома, токи в ветвях можно выразить через узловые напряжения (см. рис. 2.3):

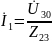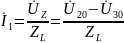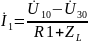или ,

или .
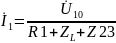