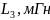СР — копия (2)
.docx
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
«ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ» (ТУСУР)
Кафедра Радиотехнических систем (РТС)
Пояснительная записка к самостоятельной работе
по дисциплине «Теория электрических цепей»
Выполнил
«__» ______ 20__ г.
Дата
Проверил
Ст.преподаватель каф. ТОР
___________А.И. Попова
«__» ______ 20__ г.
Дата
Томск 2021
Задание на расчет
Составить математические модели цепи (ММЦ) на основе заданной схемы относительно токов ветвей:
Для мгновенных значений при действии источников сигнала e(t) и j(t) произвольной формы;
Для комплексных значений при действии источников гармонических сигналов;
Для постоянных значений при действии источников постоянных сигналов
Записать уравнение баланса мощностей для мгновенных значений и для комплексных значений.
При действии постоянных источников E и J вычислить все токи и напряжения. Проверить выполнение баланса мощностей.
Вычислить значение входного сопротивления на постоянном токе и частоте
 относительно зажимов подключения
источника сигнала, заданного значением
n,
полагая значения всех остальных
источников равными нулю.
относительно зажимов подключения
источника сигнала, заданного значением
n,
полагая значения всех остальных
источников равными нулю.Рассчитать комплексное значение тока в заданной ветви схемы в установившемся режиме при действии гармонических источников сигнала методами контурных токов и узловых потенциалов.
Записать мгновенное значение искомого тока.
Вычислить значение активной и реактивной мощности в заданной ветви схемы.
Определить, при каком сопротивлении исследуемой ветви выделяемая в ней активная мощность будет максимальна. Вычислить значение этой максимальной мощности.
Основная часть
Исходные данные
Исходные данные представлены в Таблице 2.1.1 и Таблице 2.1.2.
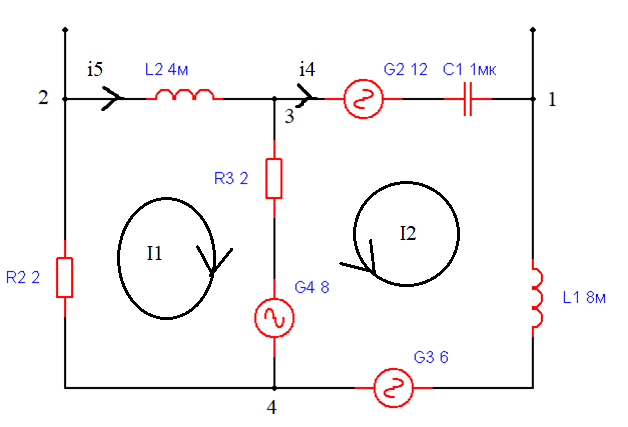
Индивидуальная схема изображена на рисунке 2.1.1.
Таблица 2.1.1 – Исходные данные (модели и параметры источников)
|
|
|
|
n |
6 |
j12 |
|
-j4 |
3 |
Таблица 2.1.2 – Исходные данные ( Параметры элементов и частота)
|
|
|
|
|
|
|
k |
4 |
2 |
2 |
8 |
4 |
8 |
500 |
0.5 |

Рисунок 2.1.1 – Индивидуальная схема
Выполнение задания
Для начала рассчитаем
 :
:

Мгновенные значения:




Постоянные значения:







Комплексные значения:








Составим ММЦ для мгновенных значений:

Составим ММЦ для постоянных значений:

Составим ММЦ для комплексных значений:
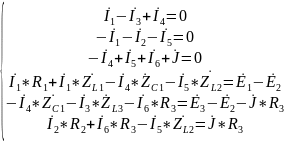
Запишем уравнение баланса мощностей для мгновенных и для комплексных значений.
Для комплексных значений:

Для мгновенных значений:

Для постоянного тока конденсатор представляет собой разрыв цепи.
Сопротивление катушки индуктивности на постоянном токе равняется нулю.
Преобразуем источник тока J в источник ЭДС:

В итоге получаем схему, изображенную на рисунке 2.2.1.

Рисунок 2.2.1 – Схема при постоянном токе
По методу контурных токов найдем все токи


Получаем матрицы:

По методу Крамера решим систему:


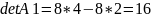




В итоге получаем токи:



Найдем напряжения:



Проверим выполнение баланса мощностей:
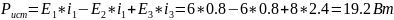


Рассчитаем входное сопротивление на постоянном токе.
При постоянном токе частота равняется нулю. Из этого следует, что сопротивление катушки будет равняться нулю, а сопротивление конденсатора стремится к бесконечности.
Схема изображена на рисунке 2.2.2

Рисунок 2.2.2 – Схема
при

Рассчитаем входное сопротивление цепи:

Рассчитаем входное сопротивление при .
При такой частоте сопротивление катушки будет стремиться к бесконечности, что представляет собой разрыв цепи, а сопротивление конденсатора равняться нулю.
Схема изображена на рисунке 2.2.3
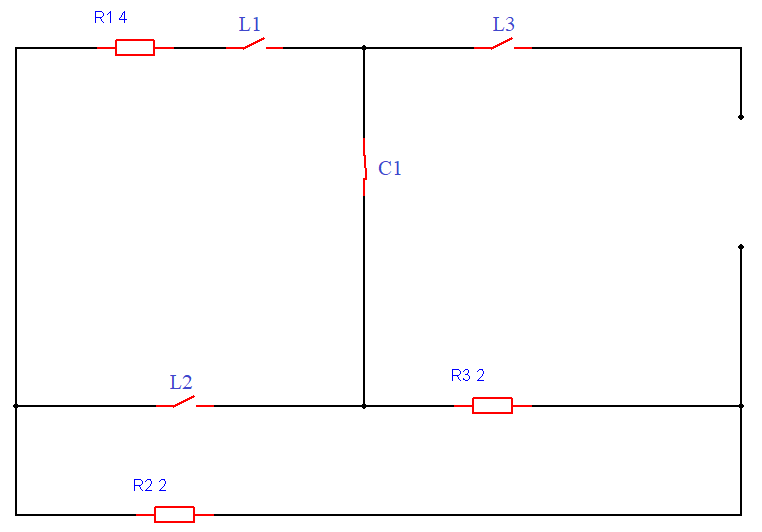
Рисунок 2.2.3 – Схема при
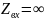
Найдем все комплексные токи в цепи.
Составим уравнения по методу контурных токов:

Воспользуемся математической средой MathCAD.

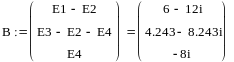

В итоге получаем токи:






Выполним проверку с помощью 1 закона Кирхгофа:



Найдем токи по методу узловых потенциалов:
Узел 4 заземлим,
тогда


Воспользуемся математической средой MathCAD



![]() B
B![]() B
B![]() B
B
Находим токи:





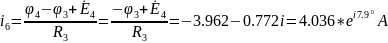
Выполним проверку с помощью 1 закона Кирхгофа:
Запишем мгновенное значение тока
 :
:

Вычислим значение активной и реактивной мощности в 1 ветви схемы:


Найдем ток i1 по методу эквивалентного генератора. Согласно методу получим схему, изображенную на рисунке 2.2.4.

Рисунок 2.2.4 – Схема эквивалентного генератора
Искомый ток i1 находится по закону Ома для полной цепи:

Для нахождения тока нужно узнать Eэг и Rэг.
Для того чтобы найти эквивалентную ЭДС, нужно рассмотреть режим холостого хода генератора, другими словами нужно отсоединить исследуемую ветвь 1, тем самым избавив генератор от нагрузки, после чего он будет работать на так называемом холостом ходу.
Преобразованная схема показана на рисунке 2.2.5.
 .
.
Рисунок 2.2.5 – Схема эквивалентного генератора
Найдем
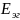 .
.
Для этого узнаем падение напряжения на L2 и C1

Найдем токи
 и
и
 по методу контурных токов.
по методу контурных токов.

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Теперь найдем Rэг, для этого примем сопротивление ЭДС источников равным нулю. Исходя из этого, получим схему, изображенную на рисунке 2.2.6.

Рисунок 2.2.6 – Схема для расчета сопротивления
При последовательном
соединении
 и
и
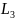 на частоте
на частоте
 возникает резонанс. Следовательно,
реактивное сопротивление ветви содержащей
катушку индуктивности и емкостной
элемент будет равняться нулю.
возникает резонанс. Следовательно,
реактивное сопротивление ветви содержащей
катушку индуктивности и емкостной
элемент будет равняться нулю.
Рассчитаем
 :
:


Теперь найдем ток


Для нахождения
 заменим сопротивление (R1+ZL1) на
сопряженное сопротивлению эквивалентного
генератора :
заменим сопротивление (R1+ZL1) на
сопряженное сопротивлению эквивалентного
генератора :



Заключение
В ходе проделанной работы были составлены ММЦ, найдены токи цепи с помощью метода контурных токов и метода узловых потенциалов. Было вычислено входное сопротивление на постоянном и переменном токе, вычислено значение активной и реактивной мощности заданной ветви.
Сравним полученные токи.
Токи, рассчитанные методом контурных токов:






Токи, рассчитанные методом узловых потенциалов:
Токи, рассчитанные двумя методами, полностью совпали.

 ,
B
,
B ,
B
,
B ,
B
,
B ,
A
,
A