19. Графический метод решения матричной игры (2xm)

; x* = (p₁, p₂), y* = (q₁, …, q_m) – оптимальные стратегии игроков.

У каждого игрока не более двух активных стратегий.

Построим график, где по оси абсцисс отложен единичный отрезок, все точки которого – смешанные стратегии игрока А, по оси ординат – выигрыш А при использовании данной смешанной стратегии. Построим график выигрыша А у(х) при использовании В всех его стратегий.

y = a_1i + (a_2i – a_1i); 1 < i < m

Тогда: p₂ = x, p₁ = 1 – x, где x – абсцисса точки максимума нижней огибающей. Цена игры V – ордината этой точки.

Стратегии игрока B, соответствующие двум прямым, образовавшим максимум нижней огибающей, являются активными. Отбросив остальные, можно решать игру как 2х2.

q_i = ; q_j = ; q_k = 0

i, j – активные стратегии В, k – неактивные стратегии В (все, кроме i и j)

20. Графический метод решения матричной игры (nx2)

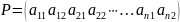; x* = (p₁, …, p_n), y* = (q₁, q₂) – оптимальные стратегии игроков.

У каждого игрока не более двух активных стратегий.

Построим график, где по оси абсцисс отложен единичный отрезок, все точки которого – смешанные стратегии игрока В, по оси ординат – выигрыш А (проигрыш В) при использовании данной смешанной стратегии. Построим график выигрыша А у(х) при использовании А всех его стратегий.

y = a_j1 + (a_j2 – a_j1); 1 < j < n

Тогда: q₂ = x, q₁ = 1 – x, где x – абсцисса точки минимума верхней огибающей. Цена игры V – ордината этой точки.

Стратегии игрока А, соответствующие двух прямым, образовавшим минимум верхней огибающей, являются активными. Отбросив остальные, можно решать игру как 2х2.

p_i = ; p_j = ; p_k = 0

i, j – активные стратегии A, k – неактивные стратегии A (все, кроме i и j)

21. Активные (существенные) стратегии игроков. Теоремы об активных стратегиях.

Активная стратегия – чистая стратегия игрока, которая входит в его оптимальную смешанную стратегию с ненулевой вероятностью.

Теорема об активных стратегиях: Если один из игроков придерживается своей оптимальной смешанной стратегии, а второй игрок не выходит за пределы своих активных стратегий, то выигрыш остаётся неизменным и равным цене игры.

22.. Принцип доминирования стратегий 2х игроков. Теоремы о доминируемых стратегиях.

Сложность решений возрастает с увеличением размеров матрицы, поэтому следует анализировать матрицу, чтобы сократить её. При анализе анализе можно выявить повторяющиеся или не выгодные стратегии.

1. A_i доминирует над A_l если: a_ij >=a_lj , для все j;

2. Доминирование в смешанных стратегиях x’A >= x’’ в (m*n) если бля всех чистых стратегий: x’a^j >=x’’a^j, для всех j;

x’ = (p₁’, … , p_n’) , a^j = (a_1j; … ; a_nj)- столбец;

3. B_i доминирует над B_j если: b_li <= b_lj , для все l;

4. Доминирование в смешанных стратегиях y’B <= y’’ в (m*n) если бля всех чистых стратегий: a_iy’<=a_iy’’, для всех i;

y’ = (q₁, … , q_n) , a_i = (a_i1; … ; a_in)- столбец; Вычёркиваются доминируЕМЫЕ стратегии.

23.. Вполне смешанная игра. Решение матричной игры n*n методом обратной матрицы.

Допустим у нас есть матрица А. Проверяем отсутствие седловых точек и чтобы det A не равен 0. Далее находим обратную матрицу. Дёмин искал злоебучим способом, мы же решали проще – нужно сделать транспонированную матрицу алгебраических дополнений и разделить её на det A (справка – если матрица 3*3, то для элемента i.j мы вычёркиваем i-тую строчку и j-тый столбец, далее находим решение оставшейся матрицы. Полученную матрицу транспонируем – столбцы становятся строками. Далее e нечётных элементов ставят знак минус. И в конце концов подписываем 1/det А перед матрицей, который потом сократится). Это и будет A^-1. Далее x* = U*A^-1/(U*A^-1*U^T) и y* = A^-1*U^T/(U*A^-1*U^T), где U – единичный вектор строка, U^T- единичный вектор столбец. В знаменателе должно получиться ЧИСЛО. Цена игры: v = 1/(U*A^-1*U^T).